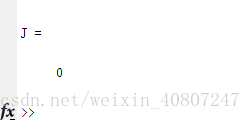五、Octave教程(Octave Tutorial)

5.1 基本操作

參考視訊: 5 - 1 - Basic Operations (14 min).mkv

在這段視訊中，我將教你一種程式語言：Octave語言。你能夠用它來非常迅速地實現這門課中我們已經學過的，或者將要學的機器學習演算法。

過去我一直嘗試用不同的程式語言來教授機器學習，包括C++、Java、Python、Numpy和Octave。我發現當使用像Octave這樣的高階語言時，學生能夠更快更好地學習並掌握這些演算法。事實上，在矽谷，我經常看到進行大規模的機器學習專案的人，通常使用的程式語言就是Octave。

Octave是一種很好的原始語言(prototyping language)，使用Octave你能快速地實現你的演算法，剩下的事情，你只需要進行大規模的資源配置，你只用再花時間用C++或Java這些語言把演算法重新實現就行了。開發專案的時間是很寶貴的，機器學習的時間也是很寶貴的。所以，如果你能讓你的學習演算法在Octave上快速的實現，基本的想法實現以後，再用C++或者Java去改寫，這樣你就能節省出大量的時間。

據我所見，人們使用最多的用於機器學習的原始語言是Octave、MATLAB、Python、NumPy 和R。

Octave很好，因為它是開源的。當然MATLAB也很好，但它不是每個人都買得起的。貌似國內學生喜歡用收費的matlab，matlab功能要比Octave強大的多，網上有各種D版可以下載。這次機器學習課的作業也是用matlab的。如果你能夠使用MATLAB，你也可以在這門課裡面使用。

如果你會Python、NumPy或者R語言，我也見過有人用 R的，據我所知，這些人不得不中途放棄了，因為這些語言在開發上比較慢，而且，因為這些語言如：Python、NumPy的語法相較於Octave來說，還是更麻煩一點。正因為這樣，所以我強烈建議不要用NumPy或者R來完整這門課的作業，我建議在這門課中用Octave來寫程式。

本視訊將快速地介紹一系列的命令，目標是迅速地展示，通過這一系列Octave的命令，讓你知道Octave能用來做什麼。

啟動Octave：

現在開啟Octave，這是Octave命令列。

現在讓我示範最基本的Octave程式碼：

輸入5 + 6，然後得到11。

輸入3 – 2、5×8、1/2、2^6等等，得到相應答案。

這些都是基本的數學運算。

你也可以做邏輯運算，例如 1==2，計算結果為 false ( 假)，這裡的百分號命令表示註釋，1==2 計算結果為假，這裡用0表示。

請注意，不等於符號的寫法是這個波浪線加上等於符號 ( ~= )，而不是等於感嘆號加等號( != )，這是和其他一些程式語言中不太一樣的地方。

讓我們看看邏輯運算 1 && 0，使用雙&符號表示邏輯與，1 && 0判斷為假，1和0的或運算 1 || 0，其計算結果為真。

還有異或運算 如XOR ( 1, 0 )，其返回值為1

從左向右寫著 Octave 324.x版本，是預設的Octave提示，它顯示了當前Octave的版本，以及相關的其它資訊。

如果你不想看到那個提示，這裡有一個隱藏的命令

輸入命令

現在命令提示已經變得簡化了。

接下來，我們將談到Octave的變數。

現在寫一個變數，對變數A賦值為3，並按下回車鍵，顯示變數A等於3。

如果你想分配一個變數，但不希望在螢幕上顯示結果，你可以在命令後加一個分號，可以抑制列印輸出，敲入回車後，不列印任何東西。

其中這句命令不列印任何東西。

現在舉一個字串的例子：變數b等於"hi"。

C等於3大於等於1，所以，現在C變數的值是真。

如果你想打印出變數，或顯示一個變數，你可以像下面這麼做：

設定A等於圓周率π，如果我要列印該值，那麼只需鍵入A像這樣 就打印出來了。

對於更復雜的螢幕輸出，也可以用DISP命令顯示：

這是一種，舊風格的C語言語法，對於之前就學過C語言的同學來說，你可以使用這種基本的語法來將結果列印到螢幕。

例如 sprintf命令的六個小數：0.6%f ,a，這應該列印π的6位小數形式。

也有一些控制輸出長短格式的快捷命令：

下面，讓我們來看看向量和矩陣：

比方說 建立一個矩陣A

對A矩陣進行賦值

考慮到這是一個三行兩列的矩陣

你同樣可以用向量

建立向量V並賦值1 2 3，V是一個行向量，或者說是一個3 ( 列 )×1 ( 行 )
的向量，或者說，一行三列的矩陣。

如果我想，分配一個列向量，我可以寫“1;2;3”，現在便有了一個3 行 1 列
的向量，同時這是一個列向量。

下面是一些更為有用的符號，如：

V=1：0.1：2

這個該如何理解呢：這個集合V是一組值，從數值1開始，增量或說是步長為0.1，直到增加到2，按照這樣的方法對向量V操作，可以得到一個行向量，這是一個1行11列的矩陣，其矩陣的元素是1
1.1 1.2 1.3，依此類推，直到數值2。

我也可以建立一個集合V並用命令“1:6”進行賦值，這樣V就被賦值了1至6的六個整數。

這裡還有一些其他的方法來生成矩陣

例如“ones(2, 3)”，也可以用來生成矩陣：

元素都為2，兩行三列的矩陣，就可以使用這個命令：

你可以把這個方法當成一個生成矩陣的快速方法。

w為一個一行三列的零矩陣，一行三列的A矩陣裡的元素全部是零：

還有很多的方式來生成矩陣。

如果我對W進行賦值，用Rand命令建立一個一行三列的矩陣，因為使用了Rand命令，則其一行三列的元素均為隨機值，如“rand(3,3)”命令，這就生成了一個3×3的矩陣，並且其所有元素均為隨機。

數值介於0和1之間，所以，正是因為這一點，我們可以得到數值均勻介於0和1之間的元素。

如果，你知道什麼是高斯隨機變數，或者，你知道什麼是正態分佈的隨機變數，你可以設定集合W，使其等於一個一行三列的N矩陣，並且，來自三個值，一個平均值為0的高斯分佈，方差或者等於1的標準偏差。

還可以設定地更復雜：

並用hist命令繪製直方圖。

繪製單位矩陣：

如果對命令不清楚，建議用help命令：

以上講解的內容都是Octave的基本操作。希望你能通過上面的講解，自己練習一些矩陣、乘、加等操作，將這些操作在Octave中熟練運用。

在接下來的視訊中，將會涉及更多複雜的命令，並使用它們在Octave中對資料進行更多的操作。

5.2 移動資料

參考視訊: 5 - 2 - Moving Data Around (16 min).mkv

在這段關於 Octave的輔導課視訊中，我將開始介紹如何在 Octave 中移動資料。

如果你有一個機器學習問題，你怎樣把資料載入到 Octave 中？

怎樣把資料存入一個矩陣？

如何對矩陣進行相乘？

如何儲存計算結果？

如何移動這些資料並用資料進行操作？

進入我的 Octave 視窗，

我鍵入 A，得到我們之前構建的矩陣 A，也就是用這個命令生成的：

A = [1 2; 3 4; 5 6]

這是一個3行2列的矩陣，Octave 中的 size() 命令返回矩陣的尺寸。

所以 size(A) 命令返回3 2

實際上，size() 命令返回的是一個 1×2 的矩陣，我們可以用 sz 來存放。

設定 sz = size(A)

因此 sz 就是一個1×2的矩陣，第一個元素是3，第二個元素是2。

所以如果鍵入 size(sz) 看看 sz 的尺寸，返回的是1 2，表示是一個1×2的矩陣，1 和 2分別表示矩陣sz的維度 。

你也可以鍵入 size(A, 1)，將返回3，這個命令會返回A 矩陣的第一個元素，A矩陣的第一個維度的尺寸，也就是 A 矩陣的行數。

同樣，命令 size(A, 2)，將返回2，也就是 A 矩陣的列數。

如果你有一個向量 v，假如 v = [1 2 3 4]，然後鍵入length(v)，這個命令將返回最大維度的大小，返回4。

你也可以鍵入 length(A)，由於矩陣A是一個3×2的矩陣，因此最大的維度應該是3，因此該命令會返回3。

但通常我們還是對向量使用 length 命令，而不是對矩陣使用 length 命令，比如
length([1;2;3;4;5])，返回5。

如何在系統中載入資料和尋找資料：

當我們開啟 Octave 時，我們通常已經在一個預設路徑中，這個路徑是 Octave的安裝位置，pwd 命令可以顯示出Octave 當前所處路徑。

cd
命令，意思是改變路徑，我可以把路徑改為C:\Users\ang\Desktop，這樣當前目錄就變為了桌面。

如果鍵入 ls，ls 來自於一個 Unix 或者 Linux 命令，ls
命令將列出我桌面上的所有路徑。

事實上，我的桌面上有兩個檔案：featuresX.dat 和priceY.dat，是兩個我想解決的機器學習問題。

featuresX
檔案如這個視窗所示，是一個含有兩列資料的檔案，其實就是我的房屋價格資料，資料集中有47行，第一個房子樣本，面積是2104平方英尺，有3個臥室，第二套房子面積為1600，有3個臥室等等。

priceY這個檔案就是訓練集中的價格資料，所以 featuresX 和priceY
就是兩個存放資料的文件，那麼應該怎樣把資料讀入 Octave 呢？我們只需要鍵入featuresX.dat，這樣我將載入了 featuresX 檔案。同樣地我可以載入priceY.dat。其實有好多種辦法可以完成，如果你把命令寫成字串的形式
load('featureX.dat')，也是可以的，這跟剛才的命令效果是相同的，只不過是把檔名寫成了一個字串的形式，現在檔名被存在一個字串中。Octave中使用引號來表示字串。

另外 who 命令，能顯示出 在我的 Octave工作空間中的所有變數

所以我可以鍵入featuresX 回車，來顯示 featuresX

這些就是存在裡面的資料。

還可以鍵入 size(featuresX)，得出的結果是 47 2，代表這是一個47×2的矩陣。

類似地，輸入 size(priceY)，結果是 47
1，表示這是一個47維的向量，是一個列矩陣，存放的是訓練集中的所有價格 Y 的值。

who 函式能讓你看到當前工作空間中的所有變數，同樣還有另一個 whos命令，能更詳細地進行檢視。

同樣也列出我所有的變數，不僅如此，還列出了變數的維度。

double 意思是雙精度浮點型，這也就是說，這些數都是實數，是浮點數。

如果你想刪除某個變數，你可以使用 clear 命令，我們鍵入 clear featuresX，然後再輸入 whos 命令，你會發現 featuresX 消失了。

另外，我們怎麼儲存資料呢？

我們設變數 v= priceY(1:10)

這表示的是將向量 Y 的前10個元素存入 v 中。

假如我們想把它存入硬碟，那麼用 save hello.mat v 命令，這個命令會將變數v存成一個叫 hello.mat 的檔案，讓我們回車，現在我的桌面上就出現了一個新檔案，名為hello.mat。

由於我的電腦裡同時安裝了 MATLAB，所以這個圖示上面有 MATLAB的標識，因為作業系統把檔案識別為 MATLAB檔案。如果在你的電腦上圖示顯示的不一樣的話，也沒有關係。

現在我們清除所有變數，直接鍵入clear，這樣將刪除工作空間中的所有變數，所以現在工作空間中啥都沒了。

但如果我載入 hello.mat 檔案，我又重新讀取了變數 v，因為我之前把變數
v存入了hello.mat 檔案中，所以我們剛才用 save命令做了什麼。這個命令把資料按照二進位制形式儲存，或者說是更壓縮的二進位制形式，因此，如果v
是很大的資料，那麼壓縮幅度也更大，佔用空間也更小。如果你想把資料存成一個人能看懂的形式，那麼可以鍵入：

save hello.txt v -ascii

這樣就會把資料存成一個文字文件，或者將資料的 ascii 碼存成文字文件。

我鍵入了這個命令以後，我的桌面上就有了 hello.txt檔案。如果開啟它，我們可以發現這個文字文件存放著我們的資料。

這就是讀取和儲存資料的方法。

接下來我們再來講講操作資料的方法：

假如 A 還是那個矩陣

跟剛才一樣還是那個 3×2 的矩陣，現在我們加上索引值，比如鍵入 A(3,2)

這將索引到A 矩陣的 (3,2) 元素。這就是我們通常書寫矩陣的形式，寫成 A 32，3和2分別表示矩陣的第三行和第二列對應的元素，因此也就對應 6。

我也可以鍵入A(2,:) 來返回第二行的所有元素，冒號表示該行或該列的所有元素。

類似地，如果我鍵入 A(:,2)，這將返回 A 矩陣第二列的所有元素，這將得到 2 4 6。

這表示返回A 矩陣的第二列的所有元素。

你也可以在運算中使用這些較為複雜的索引。

我再給你展示幾個例子，可能你也不會經常使用，但我還是輸入給你看 A([1 3],:)，這個命令意思是取 A 矩陣第一個索引值為1或3的元素，也就是說我取的是A矩陣的第一行和第三行的每一列，冒號表示的是取這兩行的每一列元素，即：

可能這些比較複雜一點的索引操作你會經常用到。

我們還能做什麼呢？依然是 A 矩陣，A(:,2) 命令返回第二列。

你也可以為它賦值，我可以取 A 矩陣的第二列，然後將它賦值為10 11 12，我實際上是取出了 A 的第二列，然後把一個列向量[10;11;12]賦給了它，因此現在 A 矩陣的第一列還是 1 3 5，第二列就被替換為 10 11 12。

接下來一個操作，讓我們把 A 設為A = [A, [100; 101;102]]，這樣做的結果是在原矩陣的右邊附加了一個新的列矩陣，就是把 A矩陣設定為原來的 A 矩陣再在右邊附上一個新新增的列矩陣。

最後，還有一個小技巧，如果你就輸入 A(:)，這是一個很特別的語法結構，意思是把 A
中的所有元素放入一個單獨的列向量，這樣我們就得到了一個 9×1 的向量，這些元素都是
A 中的元素排列起來的。

再來幾個例子：

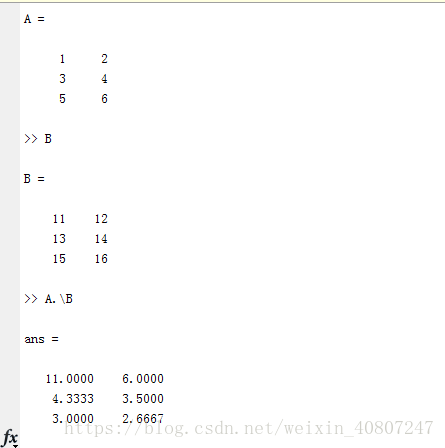
我還是把 A 重新設為 [1 2; 3 4; 5 6]，我再設一個 B為[11 12; 13 14; 15 16]，我可以新建一個矩陣 C，C = [A B]，這個意思就是把這兩個矩陣直接連在一起，矩陣
A 在左邊，矩陣 B 在右邊，這樣組成了 C 矩陣，就是直接把 A 和 B 合起來。

我還可以設C = [A; B]，這裡的分號表示把分號後面的東西放到下面。所以，[A;B]的作用依然還是把兩個矩陣放在一起，只不過現在是上下排列，所以現在 A 在上面 B在下面，C 就是一個 6×2 矩陣。

簡單地說，分號的意思就是換到下一行，所以 C 就包括上面的A，然後換行到下面，然後在下面放上一個 B。

另外順便說一下，這個[A B]命令跟 [A, B] 是一樣的，這兩種寫法的結果是相同的。

通過以上這些操作，希望你現在掌握了怎樣構建矩陣，也希望我展示的這些命令能讓你很快地學會怎樣把矩陣放到一起，怎樣取出矩陣，並且把它們放到一起，組成更大的矩陣。

通過幾句簡單的程式碼，Octave能夠很方便地很快速地幫助我們組合複雜的矩陣以及對資料進行移動。這就是移動資料這一節課。

我認為對你來講，最好的學習方法是，下課後複習一下我鍵入的這些程式碼好好地看一看，從課程的網上把程式碼的副本下載下來，重新好好看看這些副本，然後自己在Octave 中把這些命令重新輸一遍，慢慢開始學會使用這些命令。

當然，沒有必要把這些命令都記住，你也不可能記得住。你要做的就是，瞭解一下你可以用哪些命令，做哪些事。這樣在你今後需要編寫學習演算法時，如果你要找到某個Octave中的命令，你可能回想起你之前在這裡學到過，然後你就可以查詢課程中提供的程式副本，這樣就能很輕鬆地找到你想使用的命令了。

5.3 計算資料

參考視訊: 5 - 3 - Computing on Data (13 min).mkv

現在，你已經學會了在Octave中如何載入或儲存資料，如何把資料存入矩陣等等。在這段視訊中，我將介紹如何對資料進行運算，稍後我們將使用這些運算操作來實現我們的學習演算法。

這是我的 Octave視窗，我現在快速地初始化一些變數。比如設定A為一個3×2的矩陣，設定B為一個3 ×2矩陣，設定C為2 × 2矩陣。

我想算兩個矩陣的乘積，比如說 A × C，我只需鍵入A×C，這是一個 3×2 矩陣乘以 2×2矩陣，得到這樣一個3×2矩陣。

你也可以對每一個元素，做運算 方法是做點乘運算A .\*B，這麼做Octave將矩陣 A中的每一個元素與矩陣 B 中的對應元素相乘

A .\* B

B./A意思是B點除以A，而B.\A是A除以B
matlab裡的除分為左除和右除之分，也就是上面兩種。
對於矩陣的乘除都是直接的A/B或B\A或A*B,沒有點
而加點的是對於矩陣裡每個元素的乘除，也就是A./B,B.\A和A.*B

你的問題就是點除，和左除、右除的區分問題

這裡第一個元素1乘以11得到11，第二個元素2乘以12得到24，這就是兩個矩陣的元素位運算。通常來說，在Octave中點號一般用來表示元素位運算。

這裡是一個矩陣A，這裡我輸入A .\^ 2，這將對矩陣A中每一個元素平方。

我們設V是一個向量，設V為 [1; 2; 3] 是列向量，你也可以輸入1 ./V，得到每一個元素的倒數，所以這樣一來，就會分別算出 1/1 1/2 1/3。

矩陣也可以這樣操作，1 ./ A 得到A中每一個元素的倒數。

同樣地，這裡的點號還是表示對每一個元素進行操作。

我們還可以進行求對數運算，也就是對每個元素進行求對數運算。

還有自然數e的冪次運算，就是以e為底，以這些元素為冪的運算。

我還可以用 abs來對 v 的每一個元素求絕對值，當然這裡 v都是正數。我們換成另一個這樣對每個元素求絕對值，得到的結果就是這些非負的元素。還有–v，給出V中每個元素的相反數，這等價於 -1 乘以 v，一般就直接用 -v
就好了，其實就等於 -1*v。

還有一個技巧，比如說
我們想對v中的每個元素都加1，那麼我們可以這麼做，首先構造一個3行1列的1向量，然後把這個1向量跟原來的向量相加，因此
v 向量從[1 2 3] 增至 [2 3 4]。我用了一個，length(v)命令，因此這樣一來，ones(length(v) ,1) 就相當於ones(3,1)，然後我做的是v +ones(3,1)，也就是將 v 的各元素都加上這些1，這樣就將 v 的每個元素增加了1。

另一種更簡單的方法是直接用 v+1，v + 1 也就等於把 v 中的每一個元素都加上1。

現在，讓我們來談談更多的操作。

矩陣A 如果你想要求它的轉置，那麼方法是用A’,將得出 A 的轉置矩陣。當然，如果我寫(A’)’，也就是 A 轉置兩次，那麼我又重新得到矩陣 A。

還有一些有用的函式，比如： a=[1 15 2 0.5]，這是一個1行4列矩陣，val=max(a)，這將返回A矩陣中的最大值15。

我還可以寫 [val, ind] =max(a)，這將返回a矩陣中的最大值存入val，以及該值對應的索引，元素15對應的索引值為2
存入ind，所以 ind 等於2

特別注意一下，如果你用命令 max(A)，A是一個矩陣的話，這樣做就是對每一列求最大值。

我們還是用這個例子，這個 a 矩陣a=[1 15 2 0.5]，如果輸入a\<3，這將進行逐元素的運算，所以元素小於3的返回1，否則返回0。

因此，返回[1 1 0 1]。也就是說，對a矩陣的每一個元素與3進行比較，然後根據每一個元素與3的大小關係，返回1和0表示真與假。

如果我寫 find(a<3)，這將告訴我a 中的哪些元素是小於3的。

（1）返回向量中非零元素的位置 find(A)

我們以向量A=[0 1 2 3 4 5 6 7 8] 為例，在MATLAB主視窗中輸入如下命令：

A = [0 1 2 3 4 5 6 7 8];

find(A)

將會得到

ans = 

2 3 4 5 6 7 8 9

（2）返回矩陣中非零元素的位置 find(A)

我們以矩陣A=[1 2 0 1; 0 2 1 1; 0 0 1 1]為例，在matlab中輸入find(A)，我們會看到如下結果：

ans = 

1

4

5

8

9

10

11

12

我們可以看到，返回的值並不是我們想象的一個矩陣的形式，仔細觀察我們可以看到，如果我們逐列將A的元素進行排序，那麼 1 0 0 2 2 0 0 1 1 1 1 1 ，可以看到非零元素位置整好是返回結果的值，一定要注意！所以，當find函式引數為矩陣時，返回的是如上形式的結果！

設A = magic(3)，magic 函式將返回一個矩陣，稱為魔方陣或幻方 (magic squares)，它們具有以下這樣的數學性質：它們所有的行和列和對角線加起來都等於相同的值。

當然據我所知，這在機器學習裡基本用不上，但我可以用這個方法很方便地生成一個3行3列的矩陣，而這個魔方矩陣這神奇的方形螢幕。每一行、每一列、每一個對角線三個數字加起來都是等於同一個數。

在其他有用的機器學習應用中，這個矩陣其實沒多大作用。

如果我輸入 [r,c] = find(A>=7)，這將找出所有A矩陣中大於等於7的元素，因此，r 和c分別表示行和列，這就表示，第一行第一列的元素大於等於7，第三行第二列的元素大於等於7，第二行第三列的元素大於等於7。

順便說一句，其實我從來都不去刻意記住這個 find 函式，到底是怎麼用的，我只需要會用help 函式就可以了，每當我在使用這個函式，忘記怎麼用的時候，我就可以用 help函式，鍵入 help find 來找到幫助文件。

最後再講兩個內容，一個是求和函式，這是 a 矩陣：

鍵入 sum(a)，就把 a 中所有元素加起來了。

如果我想把它們都乘起來，鍵入 prod(a)，prod 意思是product(乘積)，它將返回這四個元素的乘積。

floor(a) 是向下四捨五入，因此對於 a 中的元素0.5將被下舍入變成0。

還有 ceil(a)，表示向上四捨五入，所以0.5將上舍入變為最接近的整數，也就是1。

鍵入 type(3)，這通常得到一個3×3的矩陣，如果鍵入 max(rand(3),rand(3))，這樣做的結果是返回兩個3×3的隨機矩陣，並且逐元素比較取最大值。

假如我輸入max(A,[],1)，這樣做會得到每一列的最大值。

所以第一列的最大值就是8，第二列是9，第三列的最大值是7，這裡的1表示取A矩陣第一個維度的最大值。

相對地，如果我鍵入max(A,[],2)，這將得到每一行的最大值，所以，第一行的最大值是等於8，第二行最大值是7，第三行是9。

所以你可以用這個方法來求得每一行或每一列的最值，另外，你要知道，預設情況下max(A)返回的是每一列的最大值，如果你想要找出整個矩陣A的最大值，你可以輸入max(max(A))，或者你可以將A 矩陣轉成一個向量，然後鍵入 max(A(:))，這樣做就是把 A 當做一個向量，並返回 A向量中的最大值。

最後，讓我們把 A設為一個9行9列的魔方陣，魔方陣具有的特性是每行每列和對角線的求和都是相等的。

這是一個9×9的魔方陣，我們來求一個 sum(A,1)，這樣就得到每一列的總和，這也驗證了一個9×9的魔方陣確實每一列加起來都相等，都為369。

現在我們來求每一行的和，鍵入sum(A,2)，這樣就得到了A 中每一行的和加起來還是369。

現在我們來算A 的對角線元素的和。我們現在構造一個9×9 的單位矩陣，

鍵入 eye(9)

設為I9

然後我們要用 A逐點乘以這個單位矩陣，除了對角線元素外，其他元素都會得到0。

鍵入sum(sum(A.\*eye(9))

這實際上是求得了，這個矩陣對角線元素的和確實是369。

你也可以求另一條對角線的和也是是369。

flipup/flipud 表示向上/向下翻轉。

同樣地，如果你想求這個矩陣的逆矩陣，鍵入
pinv(A)，通常稱為偽逆矩陣，你就把它看成是矩陣 A 求逆，因此這就是 A
矩陣的逆矩陣。

設 temp = pinv(A)，然後再用temp 乘以 A，這實際上得到的就是單位矩陣，對角線為1，其他元素為0。

如何對矩陣中的數字進行各種操作，在執行完某個學習演算法之後，通常一件最有用的事情是看看你的結果，或者說讓你的結果視覺化，在接下來的視訊中，我會非常迅速地告訴你，如何很快地畫圖，如何只用一兩行程式碼，你就可以快速地視覺化你的資料，這樣你就能更好地理解你使用的學習演算法。

5.4 繪圖資料

參考視訊: 5 - 4 - Plotting Data (10 min).mkv

當開發學習演算法時，往往幾個簡單的圖，可以讓你更好地理解演算法的內容，並且可以完整地檢查下演算法是否正常執行，是否達到了演算法的目的。

例如在之前的視訊中，我談到了繪製成本函式J(θ)J(θ)，可以幫助確認梯度下降演算法是否收斂。通常情況下，繪製資料或學習演算法所有輸出，也會啟發你如何改進你的學習演算法。幸運的是，Octave有非常簡單的工具用來生成大量不同的圖。當我用學習演算法時，我發現繪製資料、繪製學習演算法等，往往是我獲得想法來改進演算法的重要部分。在這段視訊中，我想告訴你一些Octave的工具來繪製和視覺化你的資料。

我們先來快速生成一些資料用來繪圖。

如果我想繪製正弦函式，這是很容易的，我只需要輸入plot(t,y1)，並回車，就出現了這個圖：

橫軸是t變數，縱軸是y1，也就是我們剛剛所輸出的正弦函式。

讓我們設定y2

Octave將會消除之前的正弦圖，並且用這個餘弦圖來代替它，這裡縱軸cos(x)從1開始，

如果我要同時表示正弦和餘弦曲線。

我要做的就是，輸入：plot(t, y1)，得到正弦函式，我使用函式hold on，hold on函式的功能是將新的影象繪製在舊的之上

我現在繪製y2，輸入：plot(t, y2)。

我要以不同的顏色繪製餘弦函式，所以我在這裡輸入帶引號的r繪製餘弦函式，r表示所使用的顏色：plot(t,y2,’r’)，再加上命令xlabel('time')，
來標記X軸即水平軸，輸入ylabel('value')，來標記垂直軸的值。

同時我也可以來標記我的兩條函式曲線，用這個命令 legend('sin','cos')將這個圖例放在右上方，表示這兩條曲線表示的內容。最後輸入title('myplot')，在影象的頂部顯示這幅圖的標題。

如果你想儲存這幅影象，你輸入print –dpng 'myplot.png'，png是一個影象檔案格式，如果你這樣做了，它可以讓你儲存為一個檔案。

Octave也可以儲存為很多其他的格式，你可以鍵入help plot。

最後如​​果你想，刪掉這個影象，用命令close會讓這個影象關掉。

Octave也可以讓你為影象標號

你鍵入figure(1); plot(t, y1);將顯示第一張圖，繪製了變數t y1。

鍵入figure(2); plot(t, y2); 將顯示第一張圖，繪製了變數t y2。

subplot命令，我們要使用subplot(1,2,1)，它將影象分為一個1*2的格子，也就是前兩個引數，然後它使用第一個格子，也就是最後一個引數1的意思。

我現在使用第一個格子，如果鍵入plot(t,y1)，現在這個圖顯示在第一個格子。如果我鍵入subplot(1,2,2)，那麼我就要使用第二個格子，鍵入plot(t,y2)；現在y2顯示在右邊，也就是第二個格子。

最後一個命令，你可以改變軸的刻度，比如改成[0.5 1 -1 1]，輸入命令：axis([0.5 1 -1 1])也就是設定了右邊圖的x軸和y軸的範圍。具體而言，它將右圖中的橫軸的範圍調整至0.5到1，豎軸的範圍為-1到1。

你不需要記住所有這些命令，如果你需要改變座標軸，或者需要知道axis命令，你可以用Octave中用help命令瞭解細節。

最後，還有幾個命令。

Clf（清除一幅影象）。

讓我們設定A等於一個5×5的magic方陣：

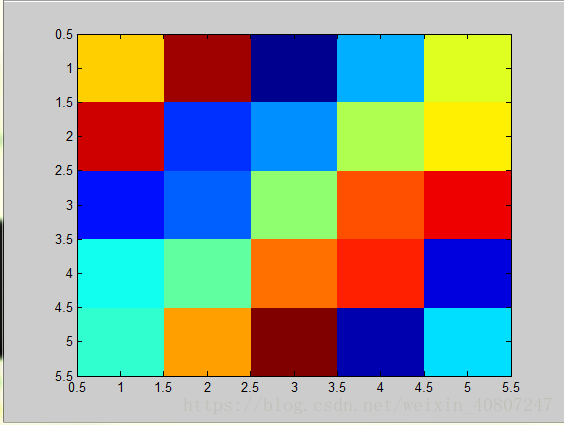
我有時用一個巧妙的方法來視覺化矩陣，也就是imagesc(A)命令，它將會繪製一個5*5的矩陣，一個5*5的彩色格圖，不同的顏色對應A矩陣中的不同值。

我還可以使用函式colorbar，讓我用一個更復雜的命令 imagesc(A)，colorbar，colormap gray。這實際上是在同一時間執行三個命令：執行imagesc，然後執行，colorbar
然後執行colormap gray。

它生成了一個顏色影象，一個灰度分佈圖，並在右邊也加入一個顏色條。所以這個顏色條顯示不同深淺的顏色所對應的值。

你可以看到在不同的方格，它對應於一個不同的灰度。

輸入imagesc(magic(15))，colorbar，colormap gray

這將會是一幅15*15的magic方陣值的圖。

最後，總結一下這段視訊。你看到我所做的是使用逗號連線函式呼叫。如果我鍵入a=1,b=2,c=3然後按Enter鍵，其實這是將這三個命令同時執行，或者是將三個命令一個接一個執行，它將輸出所有這三個結果。

這很像a=1; b=2;c=3;如果我用分號來代替逗號，則沒有輸出出任何東西。

這裡我們稱之為逗號連線的命令或函式呼叫。

用逗號連線是另一種Octave中更便捷的方式，將多條命令例如imagesc colorbar colormap，將這多條命令寫在同一行中。

現在你知道如何繪製Octave中不同的影象，在下面的視訊中，我將告訴你怎樣在Octave中，寫控制語句，比如if
while for語句，並且定義和使用函式。

5.5 控制語句：for，while，if語句

參考視訊: 5 - 5 - Control Statements_ for, while, if statements (13 min).mkv

在這段視訊中，我想告訴你怎樣為你的 Octave 程式寫控制語句。諸如："for" "while" "if" 這些語句，並且如何定義和使用方程。

我先告訴你如何使用 “for” 迴圈。

首先，我要將 v 值設為一個10行1列的零向量。

接著我要寫一個 “for" 迴圈，讓 i 等於 1 到 10，寫出來就是 i = 1:10。我要設 v(i)的值等於 2 的 i 次方，迴圈最後寫上“end”。

向量 v 的值就是這樣一個集合 2的一次方、2的二次方，依此類推。這就是我的 i 等於 1 到 10的語句結構，讓 i 遍歷 1 到 10的值。

另外，你還可以通過設定你的 indices (索引) 等於 1一直到10，來做到這一點。這時
indices 就是一個從1到10的序列。

你也可以寫 i = indices，這實際上和我直接把 i 寫到 1 到 10 是一樣。你可以寫 disp(i)，也能得到一樣的結果。所以 這就是一個 “for” 迴圈。

如果你對 “break” 和 “continue” 語句比較熟悉，Octave裡也有 “break” 和 “continue”語句，你也可以在 Octave環境裡使用那些迴圈語句。

但是首先讓我告訴你一個 while 迴圈是如何工作的：

這是什麼意思呢：我讓 i 取值從 1 開始，然後我要讓 v(i) 等於 100，再讓 i 遞增 1，直到 i 大於 5停止。

現在來看一下結果，我現在已經取出了向量的前五個元素，把他們用100覆蓋掉，這就是一個while迴圈的句法結構。

現在我們來分析另外一個例子：

這裡我將向你展示如何使用break語句。比方說 v(i) = 999，然後讓 i = i+1，當 i 等於6的時候 break (停止迴圈)，結束 (end)。

當然這也是我們第一次使用一個 if 語句，所以我希望你們可以理解這個邏輯，讓 i 等於1 然後開始下面的增量迴圈，while語句重複設定 v(i) 等於999，不斷讓i增加，然後當 i 達到6，做一箇中止迴圈的命令，儘管有while迴圈，語句也就此中止。所以最後的結果是取出向量 v 的前5個元素，並且把它們設定為999。

所以，這就是if 語句和 while 語句的句法結構。並且要注意要有end，上面的例子裡第一個 end 結束的是 if
語句，第二個 end 結束的是 while 語句。

現在讓我告訴你使用 if-else 語句：

最後，提醒一件事：如果你需要退出 Octave，你可以鍵入exit命令然後回車就會退出 Octave，或者命令quit也可以。

最後，讓我們來說說函式 (functions)，如何定義和呼叫函式。

我在桌面上存了一個預先定義的檔名為 “squarethisnumber.m”，這就是在 Octave 環境下定義的函式。

讓我們開啟這個檔案。請注意，我使用的是微軟的寫字板程式來開啟這個檔案，我只是想建議你，如果你也使用微軟的Windows系統，那麼可以使用寫字板程式，而不是記事本來開啟這些檔案。如果你有別的什麼文字編輯器也可以，記事本有時會把程式碼的間距弄得很亂。如果你只有記事本程式，那也能用。我建議你用寫字板或者其他可以編輯函式的文字編輯器。

現在我們來說如何在 Octave 裡定義函式：

這個檔案只有三行：

第一行寫著 function y = squareThisNumber(x)，這就告訴 Octave，我想返回一個 y值，我想返回一個值，並且返回的這個值將被存放於變數 y 裡。另外，它告訴了Octave這個函式有一個引數，就是引數 x，還有定義的函式體，也就是 y 等於 x 的平方。

還有一種更高階的功能，這只是對那些知道“search path (搜尋路徑)”這個術語的人使用的。所以如果你想要修改
Octave的搜尋路徑，你可以把下面這部分作為一個進階知識，或者選學材料，僅適用於那些熟悉程式語言中搜索路徑概念的同學。

你可以使用addpath 命令新增路徑，新增路徑“C:\Users\ang\desktop”將該目錄新增到Octave的搜尋路徑，這樣即使你跑到其他路徑底下，Octave依然知道會在 Users\ang\desktop目錄下尋找函式。這樣，即使我現在在不同的目錄下，它仍然知道在哪裡可以找到“SquareThisNumber” 這個函式。

但是，如果你不熟悉搜尋路徑的概念，不用擔心，只要確保在執行函式之前，先用 cd命令設定到你函式所在的目錄下，實際上也是一樣的效果。

Octave
還有一個其他許多程式語言都沒有的概念，那就是它可以允許你定義一個函式，使得返回值是多個值或多個引數。這裡就是一個例子，定義一個函式叫：

“SquareAndCubeThisNumber(x)” (x的平方以及x的立方)

這說的就是函式返回值是兩個： y1 和 y2

接下來就是y1是被平方後的結果，y2是被立方後的結果，這就是說，函式會真的返回2個值。

有些同學可能會根據你使用的程式語言，比如你們可能熟悉的C或C++，通常情況下，認為作為函式返回值只能是一個值，但
Octave 的語法結構就不一樣，可以返回多個值。

如果我鍵入 [a,b] = SquareAndCubeThisNumber(5)，然後，a 就等於25，b 就等於5的立方125。

所以說如果你需要定義一個函式並且返回多個值，這一點常常會帶來很多方便。

最後，我來給大家演示一下一個更復雜一點的函式的例子。

比方說，我有一個數據集，像這樣，資料點為[1,1], [2,2],[3,3]，我想做的事是定義一個 Octave 函式來計算代價函式 J(θ)，就是計算不同 
θ值所對應的代價函式值JJ。

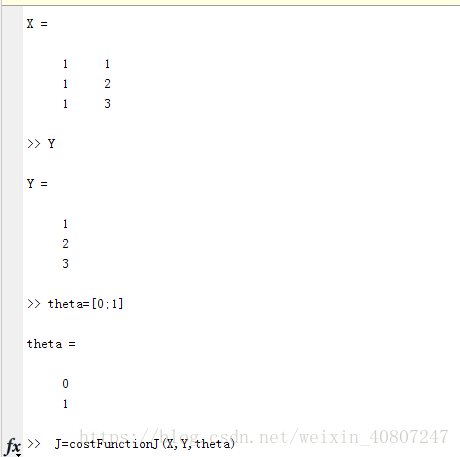
首先讓我們把資料放到 Octave 裡，我把我的矩陣設定為X = [1 1; 1 2; 1 3];

請仔細看一下這個函式的定義，確保你明白了定義中的每一步。

現在當我在 Octave 裡執行時，我鍵入JJ = costFunctionJ(X, y, theta)，它就計算出 jj等於0，這是因為如果我的資料集x 為 [1;2;3]， y 也為 [1;2;3] 然後設定 θ0θ0 等於0，θ1θ1等於1，這給了我恰好45度的斜線，這條線是可以完美擬合我的資料集的。

而相反地，如果我設定theta 等於[0;0]，那麼這個假設就是0是所有的預測值，和剛才一樣，設定θ0θ0 = 0，θ1θ1也等於0，然後我計算的代價函式，結果是2.333。實際上，他就等於1的平方，也就是第一個樣本的平方誤差，加上2的平方，加上3的平方，然後除以2m，也就是訓練樣本數的兩倍，這就是2.33。

因此這也反過來驗證了我們這裡的函式，計算出了正確的代價函式。這些就是我們用簡單的訓練樣本嘗試的幾次試驗，這也可以作為我們對定義的代價函式JJ進行了完整性檢查。確實是可以計算出正確的代價函式的。至少基於這裡的 X和 y是成立的。也就是我們這幾個簡單的訓練集，至少是成立的。

現在你知道如何在 Octave 環境下寫出正確的控制語句，比如 for 迴圈、while 迴圈和 if語句，以及如何定義和使用函式。

在接下來的Octave 教程視訊裡，我會講解一下向量化，這是一種可以使你的 Octave程式執行非常快的思想。

5.6 向量化

參考視訊: 5 - 6 - Vectorization (14 min).mkv

在這段視訊中，我將介紹有關向量化的內容，無論你是用Octave，還是別的語言，比如MATLAB或者你正在用Python、NumPy 或 Java C C++，所有這些語言都具有各種線性代數庫，這些庫檔案都是內建的，容易閱讀和獲取，他們通常寫得很好，已經經過高度優化，通常是數值計算方面的博士或者專業人士開發的。

而當你實現機器學習演算法時，如果你能好好利用這些線性代數庫，或者數值線性代數庫，並聯合調用它們，而不是自己去做那些函式庫可以做的事情。如果是這樣的話，那麼通常你會發現：首先，這樣更有效，也就是說執行速度更快，並且更好地利用你的計算機裡可能有的一些並行硬體系統等等；其次，這也意味著你可以用更少的程式碼來實現你需要的功能。因此，實現的方式更簡單，程式碼出現問題的有可能性也就越小。

舉個具體的例子：與其自己寫程式碼做矩陣乘法。如果你只在Octave中輸入a乘以b就是一個非常有效的兩個矩陣相乘的程式。有很多例子可以說明，如果你用合適的向量化方法來實現，你就會有一個簡單得多，也有效得多的程式碼。

讓我們來看一些例子：這是一個常見的線性迴歸假設函式：

如果你想要計算hθ(x)hθ(x) ，注意到右邊是求和，那麼你可以自己計算j = 0 到 j = n 的和。但換另一種方式來想想，把 hθ(x)hθ(x) 看作θTxθTx，那麼你就可以寫成兩個向量的內積，其中θθ就是θ0θ0、θ1θ1、θ2θ2，如果你有兩個特徵量，如果 n = 2，並且如果你把 x 看作x0x0、x1x1、x2x2，這兩種思考角度，會給你兩種不同的實現方式。

比如說，這是未向量化的程式碼實現方式：

計算hθ(x)hθ(x)是未向量化的，我們可能首先要初始化變數 prediction 的值為0.0，而這個變數prediction 的最終結果就是hθ(x)hθ(x)，然後我要用一個 for 迴圈，j 取值 0 到n+1，變數prediction 每次就通過自身加上 theta(j) 乘以 x(j)更新值，這個就是演算法的程式碼實現。

順便我要提醒一下，這裡的向量我用的下標是0，所以我有θ0θ0、θ1θ1、θ2θ2，但因為MATLAB的下標從1開始，在 MATLAB 中θ0θ0，我們可能會用 theta(1) 來表示，這第二個元素最後就會變成，theta(2) 而第三個元素，最終可能就用theta(3)表示，因為MATLAB中的下標從1開始，這就是為什麼這裡我的 for 迴圈，j 取值從 1 直到n+1，而不是從 0 到 n。這是一個未向量化的程式碼實現方式，我們用一個 for 迴圈對 n 個元素進行加和。

作為比較，接下來是向量化的程式碼實現：

你把x和θθ看做向量，而你只需要令變數prediction等於theta轉置乘以x，你就可以這樣計算。與其寫所有這些for迴圈的程式碼，你只需要一行程式碼，這行程式碼就是利用 Octave 的高度優化的數值，線性代數演算法來計算兩個向量θθ以及x的內積，這樣向量化的實現更簡單，它執行起來也將更加高效。這就是 Octave 所做的而向量化的方法，在其他程式語言中同樣可以實現。

讓我們來看一個C++ 的例子：

相關推薦