RSA/SHA1加密和數字簽名算法在開放平臺中的應用
加密算法
加密算法分為兩大類:1.對稱加密算法;2.非對稱加密算法。
| 密鑰個數 | 加密 | 解密 | |
|---|---|---|---|
| 對稱加密 | 一個 | 使用密鑰加密 | 使用同一個密鑰解密 |
| 非對稱加密 | 兩個,公鑰和私鑰 | 使用其中一把密鑰加密 | 使用另外一把密鑰解密 |
RSA非對稱加密算法
- RSA是目前應用最廣泛的非對稱加密算法,各種語言都支持RSA算法,如Java,Python,C++(openssl),Go(openssl),PHP(openssl),Object-C,Android,javascript等。
- 對於一個私鑰匙、有且只有一個與之對應的公鑰。公/私鑰的主流可選位長度為1024、2048、3072、4096....,越長安全系數越高。私鑰加密的內容,使用公鑰能夠解密,同樣使用公鑰加密的內容,使用私鑰也能解密。
- 在linux系統下,有兩種常用的工具用於生成RSA密鑰對,ssh-keygen和openssl genrsa。
-
RSA是一個能夠同時用於加密和數字簽名的算法,典型的應用場景:隱藏原文、防止原文被篡改、身份認證。隱藏原文是所有加密算法的通用功能(要不然怎麽叫加密),防止原文被篡改是數字簽名的功能,數據傳輸的具體流程如下:
- 甲方構建密鑰對,將公鑰交給乙方
- 甲方使用私鑰加密原文,然後將加密數據發送給乙方。乙方使用公鑰對簽名進行解密,獲取原文,如果解密失敗,則原文被篡改。
- 乙方給甲方發送原文的時候,先使用公鑰對原文加密,將加密數據發送給甲方。甲方使用私鑰對簽名解密,獲取原文,如果解密失敗,則原文被篡改。
- 如果第三方不知道密鑰對,則第三方什麽都做不了。如果第三方知道公鑰,則第三方對甲方的原文具有與乙方一樣的閱讀權限,但無法篡改甲方的原文,因為沒有私鑰,無法生成合法的數字簽名。
-
RSA對一次加密的明文的長度是有要求的,在不同的padding模式下,能加密的明文長度也不相同。以RSA 1024為例,輸入的明文的字節數不能超過鑰模長1024bits,即最長為128bytes。RSA 1024的不同padding模式下的明文長度的最大值計算公式:
- RSA_PKCS1_PADDING RSA_size(1024) - 11 = 117bytes
- RSA_PKCS1_OAEP_PADDING RSA_size(1024) - 41 = 87bytes
- RSA_NO_PADDING RSA_size(1024) = 128bytes
- 由於RSA等非對稱加密算法對原文長度有限制,且算法效率沒有對稱加密高,在實際應用中通常被用於傳遞對稱加密算法的密鑰(通常是一個隨機值),然後通信雙方使用對稱加密算法保證數據安全。
數字簽名
數字簽名是一份數據經過特定的算法計算後得出的特殊標識,用來防止數據在傳輸過程中被偽造或篡改,是非對稱加密技術與數字摘要技術的綜合應用。
數字摘要
- 數字摘要指可以將任意長度的數據,通過一個摘要算法計算得到的固定長度的數據。也就是說摘要算法可以將很長的數據變為一個固定長度的數據,通常計算得出的數據要比原始數據短得多,所以被稱為‘摘要’,典型的摘要算法有MD5和SHA1。
-
數字摘要算法具有以下重要特性:
- 原數據不同,計算得到的摘要一定不同,反之,原數據不變,計算得到的摘要一定相同。
- 無法通過摘要逆運算獲得原數據,即摘要計算不可逆。
- 任意長度的輸入數據,經過計算都會得出固定長度的摘要。
加密算法和摘要算法的區別
- 加密後的密文可以使用對應的密鑰進行解密,獲取原文;摘要是不能進行逆向解密的
- 加密之後的密文的長度不定;摘要的長度是確定的
- 非對稱加密對明文的長度有限制;摘要對明文長度無限制
應用場景
-
非對稱加密技術能夠確保只有持有密鑰對的雙方才能獲取到正確的數據,但對加密原文的長度有限制,而數字摘要算法能夠將輸入數據轉換為固定長度的摘要,並保證在原數據不變的情況下,摘要計算結果是一致的。這兩項技術的特性的結合,就形成了數字簽名的經典應用場景:
- 發送者使用MD5(或SHA1)算法提起原文摘要,然後使用私鑰對摘要進行加密,把密文與原文一起傳送給接收者。
- 接收者使用公鑰對密文進行解密,獲得摘要,然後使用與發送者一樣的摘要算法MD5(或SHA1)對原文提取摘要,比較兩個摘要是否相等
- 摘要相等,說明原文完整且沒有被篡改;不相等,說明原文不正確。
- 數字簽名有兩種作用:1. 在私鑰沒有泄漏的情況下,能夠確保數據是由發送方簽名發送的。 2.能夠確保數據是完整的且沒有被篡改。但是數據本身是否加密,並不是數字簽名的作用範疇,因為加密的是摘要,並不是數據本身。
RSA和數字簽名在Https協議通信中有經典的應用,這裏不再贅述。
RSA和數字簽名在開放平臺中的應用
在開放平臺中,RSA和數字簽名多用於開發者接入的身份驗證。
RSA的應用
-
獨立開發者接入平臺時,使用RSA算法作為開發者身份驗證的核心算法,如雲信通IM平臺即使用此種模式。開發者接入平臺時,需要如下幾個步驟:
- 創建一個應用app,平臺會分配一個SDKAPPID
- 將SDKAPPID關聯到一對RSA的公鑰和私鑰上,公鑰和私鑰由平臺生成
- 由雲信通IM平臺持有公鑰,開發者持有私鑰
- 開發者的服務每次調用平臺接口時,需要攜帶使用指定參數和私鑰生成的簽名,生成簽名的公式為:RSA(私鑰,SDKAPPID,用戶id)
- 雲平臺會驗證每次接口調用中傳入的簽名和用戶id,首先使用公鑰對簽名解密,然後驗證SDKAPPID是否合法,比對用戶id,保證用戶id不會被篡改。
- 每個簽名具有默認的有效期,也就是說,在私鑰不變的情況下,一個用戶的簽名在有效期內是可以反復使用的
- 在獨立開發者接入平臺的場景中,開發者自己需要保證私鑰的安全,且用戶登陸的驗證由開發者的後端服務來執行,平臺並不負責驗證用戶是否登陸,平臺僅需要驗證服務的調用方是否是合法的開發者。經典的交互流程如下所示:
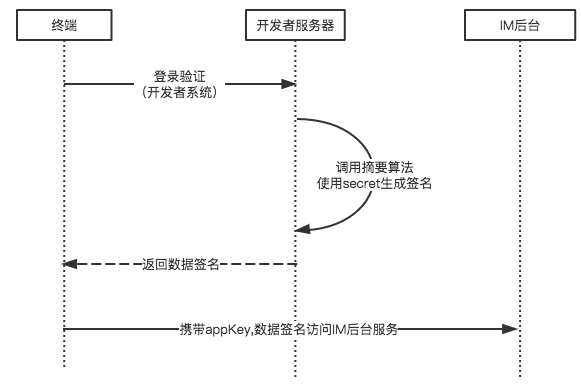
數字簽名的應用
-
SHA1哈希算法生成數字簽名也被應用於獨立開發者接入模式,如融雲開放平臺、網易雲信就使用此模式。開發者接入平臺時,需要如下幾個步驟:
- 開發者申請接入平臺,由平臺分配AppKey和Secret,Secret由開發者確保安全
-
在所有平臺服務端 API 接口的請求中,都需要附帶以下4個HTTP Request Header:
| 名稱| 類型 | 說明 | | AppKey | String | 平臺分配的 App Key | | Nonce| String | 隨機數,長度無限制 | | Timestamp | String | 時間戳 | | Signature | String | 數字簽名 | - 數字簽名是用於檢驗開發者是否合法的關鍵,其生成方式為:App Secret、Nonce (隨機數)、Timestamp (時間戳)三個字符串按先後順序拼接成一個字符串並進行 SHA1 哈希計算。
-
這種開發者接入模式中,數字簽名起到幾個作用:
- 用於驗證開發者的合法性
- 用於保證關鍵參數如AppKey,Timestamp不被篡改(前提是開發者保證了Secret的安全)
-
SHA1沒有明文長度的限制,這也是其比RSA算法有優勢的地方,但SHA1算法是摘要算法,其計算出來的結果是無法解密的。
RSA/SHA1加密和數字簽名算法在開放平臺中的應用
