前言

2.2 堆疊

2.2.1 什麼是堆疊

計算機如何進行表示式求值？

【例】算術表示式5+6/2-3*4。正確理解：

5+6/2-3*4=5+3-3*4=8-3*4=8-12=-4

• 由兩類物件構成的：
  
  • 運算數，如2、3、4
  • 運算子號，如+、- 、*、/
• 不同運算子號優先順序不一樣

字尾表示式

• 中綴表示式：運算子號位於兩個運算數之間。如：a+b*c-d/e
• 字尾表示式：運算子號位於兩個運算數之後。如：abc*+de/-

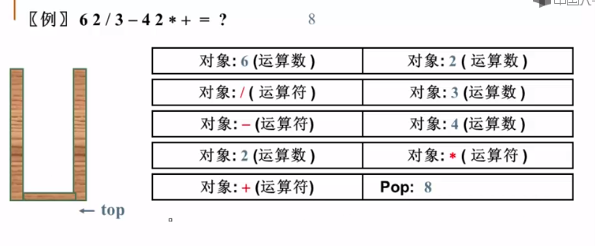
【例】62/3-42*+= ?

字尾表示式求值策略：從左向右“掃描”，逐個處理運算數和運算子號

1. 遇到運算數怎麼辦？
2. 遇到運算子號怎麼辦？

【啟示】需要有種儲存放放，能順序儲存運算數，並在需要時“倒序”輸出

堆疊的抽象資料型別描述

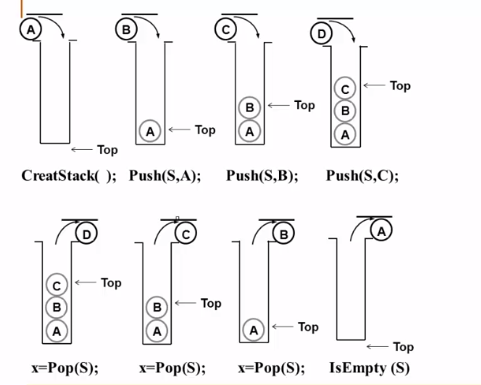
堆疊：具有一定操作約束的線性表，只在一端（棧頂，Top）做插入，刪除

• 插入資料：入棧（Push）
• 刪除資料：出棧（Pop）
• 先進後出：Last in first out（LIFO）

2.2.2 堆疊的順序儲存實現

棧的順序儲存結構通常由一個一維陣列和一個記錄棧頂元素位置的變數組成

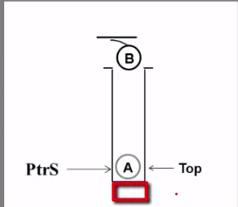
入棧

void Push(Stack PtrS,ElementType item)
{
    if(PtrS->Top==MaxSize-1)
    {
        printf("堆疊滿"
 
);
        return;
    ]
    else
    {
        PtrS->Data[++(PtrS->Top)]=item;
        return;
    }
}

入棧的影象

出棧

ElementType Pop(Stack PtrS)
{
    if(PtrS->Top==-1)
    {
        printf("堆疊空");
        return ERROR;
    }
    else
        return(PtrS->Data[(PtrS->Top--)]);
}
 

【例】請用一個數組實現兩個堆疊，要求最大地利用陣列空間，使陣列只要有控制元件入棧操作就可以成功

【分析】一種比較聰明的方法是使這兩個棧分別從陣列的兩頭開始向中間生長；當兩個棧的棧頂指標相遇時，表示兩個棧都滿了

#define MaxSize<儲存資料元素的最大個數>
struct DStack
{
    ElementType Data[MaxSize];
    int Top1;  //堆疊1的棧頂指標
    int Top2;  //堆疊2的棧頂指標
}S

S.Top1=-1;
S.Top2=MaxSize;

void Push(struct DStack *PtrS,ElementType item,int Tag)
{
    if(PtrS->Top2-PtrS->Top1==1)  //堆疊滿
    {
        printf("堆疊滿");
        return;
    }
    if(Tag==1) //對第一個堆疊操作
        PtrS->Data[++(PtrS->Top1)]==item;
    else       //對第二個堆疊操作
        PtrS->Data[--(PtrS->Top1)]==item;
}

ElementType Pop(struct DStack *PtrS,int Tag)
{
    if(Tag==1)//對第一個堆疊操作
        if(PtrS->Top1==-1) //堆疊1空
        {
            printf("堆疊1空");
            return NULL;
        }
        else
            return PtrS->Data[(PtrS->Top1)--];
    else
    {
        if(PtrS->Top2==MaxSize)
        {
            printf("堆疊2空");
            return NULL;
        }
        else
            return PtrS->Data[(PtrS->Top2)++]; 
    }
}

2.2.3 堆疊的鏈式儲存實現

棧的鏈式儲存結構實際上就是一個單鏈表，叫做鏈棧。插入和刪除操作只能在鏈棧的棧頂進行。

//鏈棧的定義
typedef struct SNode *Stack;
struct SNode
{
    ElementType Data;
    struct SNode *Next;
};

//建立一個空棧
Stack CreateStack()
{
    Stack S;
    S=(Stack)malloc(sizeof(struct SNode));
    S->Next=NULL;
    return S;
}

//判斷鏈棧是否為空
int IsEmpty(Stack S)
{
    return (S->Next==NULL);
}

//將元素item壓入堆疊S
void Push(ElementType item,Stack S)
{
    struct SNode,*TmpCell;
    TmpCell=(struct SNode *)malloc(sizeof(struct SNode));
    TmpCell->Element=item;
    TmpCell->Next=S->Next;
    S->Next=TmpCell;
}

//刪除並返回堆疊的S的棧頂元素（出棧）
ElementType Pop(Stack S)
{
    struct SNode *FirstCell;
    ElementType TopElem;
    if(IsEmpty(S))
    {
        printf("堆疊空");
        return NULL;
    }
    else
    {
        FirstCell=S->Next;
        S->Next=FirstCell->Next;
        TopElem=FirstCell->Element;
        free(FirstCell);
        return TopElem;
    }
}

2.2.4 堆疊應用：表示式求值

回憶：應用堆疊實現字尾表示式求值的基本過程：

從左到右讀入字尾表示式的各項（運算子或運算數）：

1. 運算數：入棧
2. 運算子：從堆疊中彈出適當數量的運算數，計算並結果入棧
3. 最後，堆疊頂上的元素就是表示式的結果值

中綴表示式求值

基本策略：將中綴表示式轉換為字尾表示式，然後求值

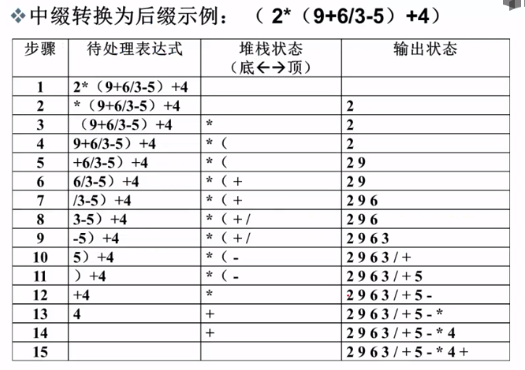
如何將中綴表示式轉換為字尾表示式？

觀察一個簡單例子：2+9/3-5 -> 2 9 3 / +5 -

• 運算數相對順序不變
• 運算子號順序發生改變
  
  • 需要儲存“等待中”的運算子號
  • 要將當前運算子號與“等待中”的最後一個運算子號比較

中綴表示式如何轉換為字尾表示式

從頭到尾讀取中綴表示式的每個物件，對不同物件按不同的情況處理。

1. 運算數：直接輸出

2. 左括號：壓入堆疊

3. 右括號：將棧頂的運算子彈出並輸出，直到遇到左括號（出棧，不輸出）

4. 運算子

   1. 若優先順序大於棧頂運算子時，則把它壓棧
   2. 若優先順序小於等於棧頂運算子時，將棧頂運算子彈出並輸出；再比較新的棧頂運算子，直到該運算子大於棧頂運算子優先順序為止，然後將該運算子壓棧

5. 若各物件處理完畢，則把堆疊中存留的運算子一併輸出

【示例】

堆疊的其他應用

• 函式呼叫及遞迴實現
• 深度優先搜尋
• 回溯演算法
• 。。。。

2.3 佇列及其實現

2.3.1 佇列及順序儲存實現

什麼是佇列

佇列：具有一定操作約束的線性表

• 插入和刪除操作：只能在一端插入，而在另一端刪除
• 資料插入：入隊（AddQ）
• 資料刪除：出佇列（DeleteQ）
• 先進先出：FIFO

佇列的抽象資料型別描述

佇列的順序儲存實現

佇列的順序儲存結構通常由一個一維陣列和一個記錄佇列頭元素位置的變數front以及一個記錄佇列尾元素位置的變數rear組成。

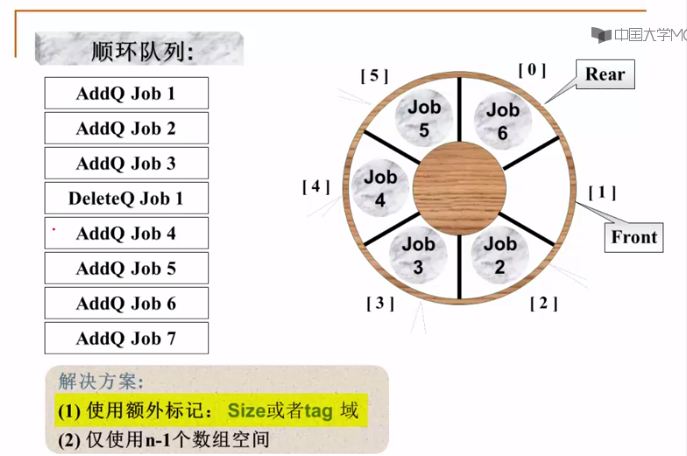
迴圈佇列

入隊

void AddQ(Queue PtrQ,ElementType item)
{
    if(PtrQ->rear+1)%MaxSize==PtrQ->front)
    {
        printf("佇列滿");
        return;
    }
    PtrQ->rear=(PtrQ->rear+1)%MaxSize;
    PtrQ->Data[PtrQ->rear]=item;
}

出隊

ElementType DeleteQ(Queue PtrQ)
{
    if(PtrQ->front==PtrQ->rear)
    {
        printf("佇列空");
        return ERROR;
    }
    else
    {
        PtrQ->front==(PtrQ->front+1)%MaxSize;
        return PtrQ->Data[PtrQ->front];
    }
}

2.3.2 佇列的鏈式儲存實現

佇列的鏈式儲存結構也可以用一個單鏈表實現。插入和刪除操作分別在連結串列的兩頭進行。

不帶頭結點的鏈式隊列出隊操作的一個示例：

ElementType DeleteQ(Queue PtrQ)
{
    struct Node *FrontCell;
    ElementType FrontElem;
    if(PtrQ->front==NULL)
    {
        printf("佇列空"）;
        return ERROR;
    }
    FrontCell=PtrQ->front;
    if(PtrQ->front==PtrQ->rear)       //若佇列只有一個元素
    {
        PtrQ->front==PtrQ->rear=NULL; //刪除後，佇列置為空
    }
    else
        PtrQ->front=PtrQ->front->Next;
    FrontElem=FrontCell->Data;
    free(FrontCell);                  //釋放被刪除結點空間
    return FrontElem;
}

2.4 應用例項：多項式加法運算

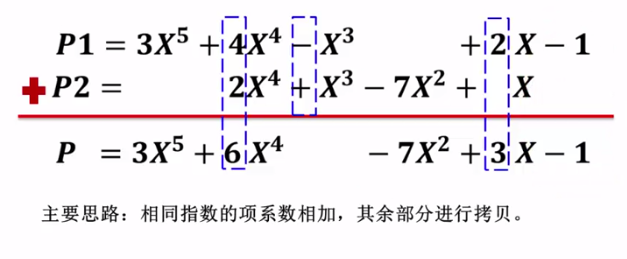
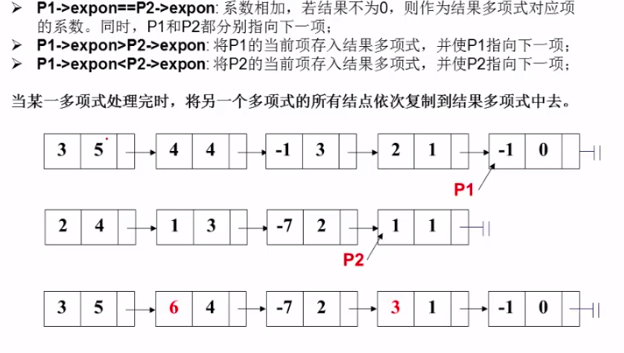
多項式加法運算

採用不帶頭結點的單向連結串列，按照指數遞減的順序排列各項

演算法思路：兩個指標p1和p2分別指向這兩個多項式第一個結點，不斷迴圈：