稀疏矩陣-壓縮儲存-列轉置法- 一次定位快速轉置法
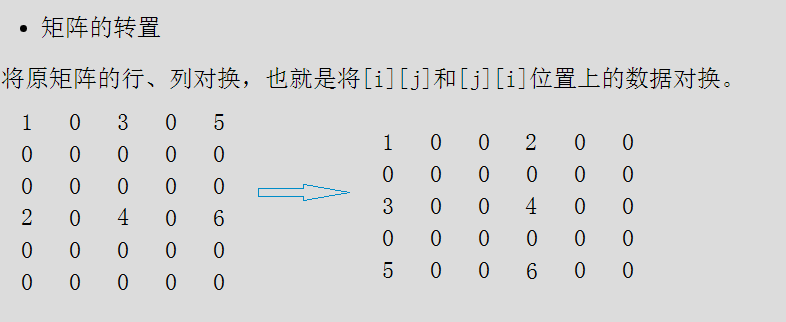
稀疏矩陣的壓縮儲存
壓縮儲存值儲存極少數的有效資料。使用{row,col,value}三元組儲存每一個有效資料,三元組按原矩陣中的位置,以行優先順序先後順序依次存放。
壓縮儲存:行優先一行一行掃 有效資料存入以為矩陣_arr
列轉置法 : 從前向後遍歷壓縮矩陣,先找列號為0的存入 轉置矩陣的壓縮矩陣.然後從前向後找列號為1的 。。。直到轉置矩陣的壓縮矩陣大小和 原矩陣的一樣大 這時就找完了
時間複雜度為 O(原矩陣列數 * 壓縮矩陣長度)
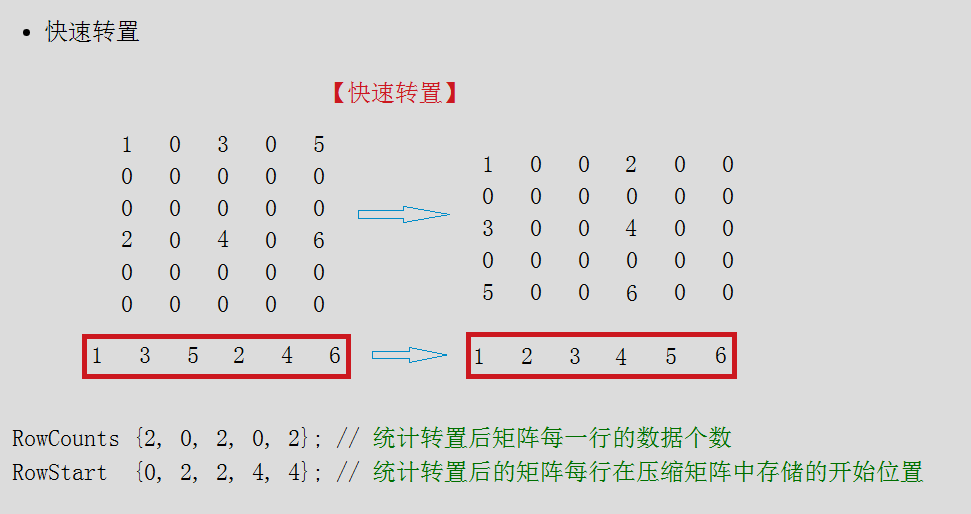
一次定位快速轉置法:
RowCounts 記錄 原矩陣每列的有效元素元素的個數 (這裡Row指的是轉置矩陣的行 RowCount指的也就是轉置矩陣 的 行有效元個數)
RowStart 記錄的是 原矩陣 每列首個有效元素 在 轉置矩陣 的壓縮矩陣中的座標 (也就是 轉置矩陣 的 每行首個有效元素 在 轉置矩陣 的壓縮矩陣中的 座標)
RowStart[n]可以由 RowCount[n-1]和上一個RowStart[n-1]求得 n>0
RowStart[0] = 0;
利用 RowStart 可以實現 由 原矩陣 的壓縮矩陣元素 到 轉置矩陣的壓縮矩陣 的一次快速定位
如:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <assert.h>
#include <vector>
#include <string>
using namespace std;
/***
*
*稀疏矩陣
*壓縮儲存
*轉置 (一般 和 快速轉置)
*2016-4-18
*bozi
******************/
//三元組
template<class T>
struct Triple
{
size_t _row;
size_t _col;
T _value;
Triple()
{}
Triple(size_t row, size_t col, T value)
:_row(row)
,_col(col)
,_value(value)
{}
};
//稀疏矩陣
template<class T>
class SparesMatrix
{
public:
SparesMatrix();
SparesMatrix(const T* array, size_t row, size_t col, const T& invalid);
SparesMatrix<T> Transport();//列轉置
SparesMatrix<T> FastTransport();//快速轉置
void Display() const;
protected:
vector<Triple<T> > _array;//動態陣列儲存稀疏矩陣
size_t _rowMatrix;
size_t _colMatrix;
T _invalid;//定義的無效值
};
template<class T>
SparesMatrix<T>::SparesMatrix()
{}
template<class T>
SparesMatrix<T>::SparesMatrix(const T* array, size_t row, size_t col, const T& invalid)
:_rowMatrix(row)
,_colMatrix(col)
,_invalid(invalid)
{
for (size_t i = 0; i < _rowMatrix; i++)
{
for (size_t j = 0; j < _colMatrix; j++)
{
if (array[i * col + j] != invalid)
{
//_array.push_back({i, j, array[i * col + j]});
_array.push_back(Triple<T>(i, j, array[i * col + j]));
}
}
}
}
template<class T>
void SparesMatrix<T>::Display()const
{
size_t arr_size = _array.size();
assert(arr_size != 0);
size_t index = 0;
for (size_t i = 0; i < _rowMatrix; i++)
{
for (size_t j = 0; j < _colMatrix; j++)
{
if (index < arr_size && _array[index]._row == i && _array[index]._col == j)
{
cout<<_array[index]._value<<"";
index++;
}
else
{
cout<<_invalid<<"";
}
}
cout<<endl;
}
cout<<endl;
}
//轉置 (列轉置法)
template<class T>
SparesMatrix<T> SparesMatrix<T>::Transport()
{
size_t arr_size = _array.size();
assert(arr_size != 0);
SparesMatrix<T> ret;
ret._rowMatrix = _colMatrix;
ret._colMatrix = _rowMatrix;
ret._invalid = _invalid;
ret._array.reserve(arr_size);//先開闢這麼大的空間 提高效率 防止後面push_back()每次不夠還要開闢
//在原來的 行優先的 陣列_array中,每次遍歷一遍,找到這次列號與對應 的列j相等的元素 將這個元素行列互換 存入ret._array
//相當於 將 原陣列的 行優先 轉化為 列優先
//原陣列的列優先 就相當於 轉置後矩陣的 行優先
for (size_t j = 0; j < _colMatrix; j++)
{
size_t index = 0;
while (index < arr_size)
{
if (_array[index]._col == j)
{
//ret._array.push_back({_array[index]._col, _array[index]._row, _array[index]._value});
ret._array.push_back(Triple<T>(_array[index]._col, _array[index]._row, _array[index]._value));
}
index++;
}
if (arr_size == ret._array.size())
{
break;
}
}
return ret;
}
template<class T>
SparesMatrix<T> SparesMatrix<T>::FastTransport()//快速轉置
{
size_t arr_size = _array.size();
assert(arr_size > 0);
size_t index = 0;
SparesMatrix<T> ret;
ret._rowMatrix = _colMatrix;
ret._colMatrix = _rowMatrix;
ret._invalid = _invalid;
ret._array.resize(arr_size);// 調整大小 (不能用reserve(只是空間變大 但Size沒變) 而resize 是調整大小 兩個都變)
// 兩張輔助表
//RowCounts記錄原矩陣 每列的 非零元素
//RowStart記錄原矩陣列優先時 每列首個非零元的 座標
//用這兩張表 可以馬上把 _array陣列中的元素 定位到 ret._array(新表)中
int* RowCounts = new int[_colMatrix];
int* RowStart = new int[_colMatrix];
memset(RowCounts, 0, _colMatrix * sizeof(int));
memset(RowStart, 0, _colMatrix * sizeof(int));
// 初始化RowCounts
for (size_t i = 0; i < arr_size; i++)
{
RowCounts[_array[i]._col]++;//【好方法 統計可以用到】由列號找到對應RowCounts
}
RowStart[0] = 0;
// 初始化 RowStart(由 RowCount 求出 RowStart)
for (size_t i = 1; i < _colMatrix; i++)//注意i 從1開始
{
RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];
}
//根據RowStart 將原矩陣_array中的元素 一次 快速 的 對應到 ret.array
for (size_t i = 0; i< arr_size; i++)
{
//ret._array[RowStart[array[i]._col]++] = {_array[i]._col, _array[i]._row, _array[i]._value};
//RowStart[_array[i]._col]++ 更新下一個元素 在 ret._array中的 位置
ret._array[RowStart[_array[i]._col]++] = Triple<T>(_array[i]._col, _array[i]._row, _array[i]._value);
}
delete[] RowCounts;
delete[] RowStart;
return ret;
}
void testSparseMatrix()
{
int array[6][5] =
{
{1, 0, 3, 0, 5 },
{0, 0, 0, 0, 0,},
{0, 0, 0, 0, 0,},
{1, 0, 3, 0, 5 },
{0, 0, 0, 0, 0,},
{0, 0, 0, 0, 0,},
};
SparesMatrix<int> s1((int*)array, 6, 5, 0);
s1.Display();
SparesMatrix<int> s2;
s2 = s1.Transport();
cout<<"轉置後的矩陣為:"<<endl;
s2.Display();
SparesMatrix<int> s3;
s3 = s1.FastTransport();
cout<<"快速轉置後的矩陣為:"<<endl;
s3.Display();
}
int main()
{
testSparseMatrix();
return 0;
}