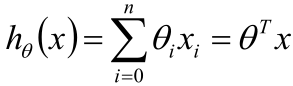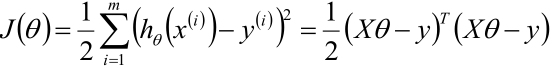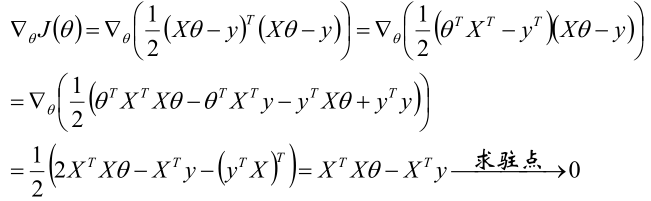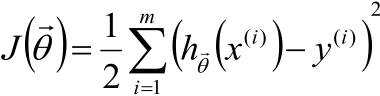前提說明：因為在做此總結之前我已總結過“感知機演算法”，而這裡的很多知識(包括預備知識)和“感知機演算法”中有重疊，所以本總結的知識不會像我做的其他教程那樣對每個知識點都做很詳細的解釋，如果你已經掌握了“感知機演算法”的相關知識，那本總結對你是沒問題的，反之，你就需要了解下“感知機演算法”了。

迴歸問題

         線性迴歸的一般形式如下：

         其中x是已知的一個個樣本點，θ是未知的權重。

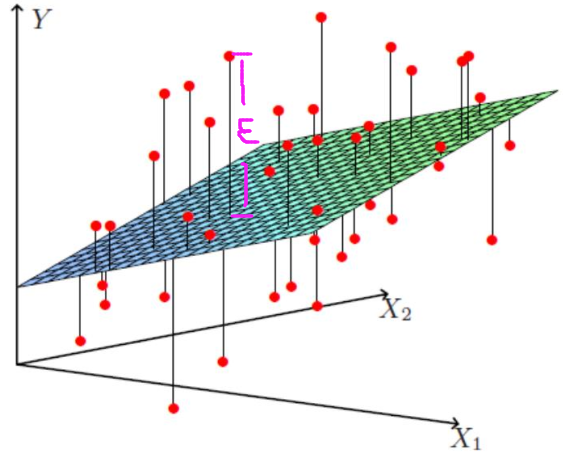
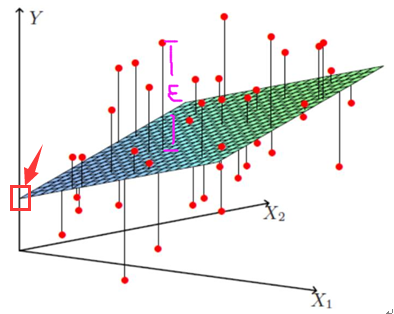
         但如下圖所示：

         上圖的每個紅點是一個個樣本點即x，上圖的平面就是迴歸後的平面即h_θ

         一般情況下，我們不可能讓h_θ(x)完全擬合數據（那樣就過擬合了），於是最終求得h_θ(x)與的每個樣本點的實際位置就有個差值(上圖粉紅色標註的那段距離)，這就是殘差。

         一般用ε表示殘差，於是h_θ(x)就更新成：

                   h_θ(x) =θ^Tx +ε

         殘差ε是獨立同分布的，因為若以賣房子為例子，那房子的價格的殘差（這裡殘差就是指：房價不是正常定價，莫名其妙的高那麼點或低那麼點）一定是定房價的那個人/團隊因為某種原因這麼做的，而既然出自一個人/團隊之手，那所有的殘差一定符合這個人/團隊的考慮吧，於是就屬於這個人/團隊的分佈 -- 屬於同一個分佈，而每個房子和房子的殘差是沒關係的（隔壁房子就是精裝修，那和你想買的房子有半毛錢關係？）-- 獨立，所以殘差是獨立同分布。

         不過這個殘差到底是什麼分佈呢？

         答案是：服從均指為0，方差為某個定值σ²的高斯分佈。其理論依據是：中心極限定理。

如何求θ

         下面的問題是如何求θ，步驟如下：

                   1，利用最小二乘法的知識寫出θ的目標函式

                            PS：h_θ(x⁽ⁱ⁾)可以寫成所有樣本資料組成的矩陣X乘上樣本權值θ的向量的形式，而如果h_θ(x)寫成了這樣的形式，那y⁽ⁱ⁾也需要用一個向量y表達，第二個等號就是這樣來的。

                   2，對J(θ)求梯度後令梯度=0來求駐點。

                   3，得到結果

                            θ= (X^TX)^-1X^Ty

                            PS：這個結果有個簡單的記法(可以這樣記，但一旦有人問這個結果的來歷，可不能這樣回答)：Xθ= y  =>  X^TXθ= X^Ty  =>  θ= (X^TX)^-1X^Ty

         話說，有時為了防止過擬合和防止X^TX不可逆(樣本個數<維度)的情況，增加λ擾動

                   θ= (X^TX+λI)^-1X^Ty，I是單位陣

廣義逆矩陣(偽逆)

         一般若矩陣是方陣的話可以求其逆矩陣，如，若x是個方陣則：

                   xθ= y  =>  θ= x^-1y

         但若x不是方陣，那上面的轉換就不行了，這時就要用到偽逆了。

         什麼是偽逆？看上面“如何求θ”的結果，即對於：

                   xθ= y  =>  θ= (x^Tx)^-1x^Ty

         這時(x^Tx)^-1x^T就起到了x^-1的作用，因此就把(X^TX)^-1X^T稱作廣義逆矩陣，簡稱偽逆，用x⁺表示。

         總結一下：

                   若x為可逆方陣，(x^Tx)^-1x^T即為x^-1，因為：

                            (x^Tx)^-1x^T= x^-1(x^T)^-1x^T = x^-1

若A為矩陣(非方陣)時，稱x⁺為x的廣義逆矩陣(偽逆)。

線性迴歸的複雜度懲罰因子

         話說，對於線性迴歸的目標函式

                   式1

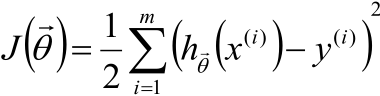
         我們是不希望每個θ特別大，因為這樣一來θ_iX⁽ⁱ⁾的值就會就會差距很大，這樣對每個樣本預測的結果h_θ(x⁽ⁱ⁾)就會波動的很厲害。因此，我們的目標還得多一個：讓每個θ都儘可能的趨近於0，於是給目標函式增加θ的平方和損失成為了下面的形式：

                   式2

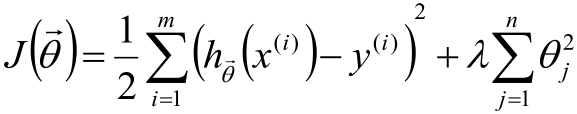
                  PS：這裡假設θ服從高斯分佈。

         為了更有概念，這裡還以房價預測舉個例子：假設我們通過某種方式蒐集到了“房屋大小、房屋朝向、小區環境、交通情況”等10W個特徵，這時如果每個θ都不為0且很大的話，那這個模型是很龐大的，但可能有些特徵對房價預測的影響度太小以至於可以忽略不計的話，那就讓這些樣本對應的θ= 0，這樣一來這些特徵就成功的被模型忽略了，從而達到對模型降維的目的！

         最後在從新說一遍，式1是標準的損失函式，式2中多出來的那一塊中除去λ的部分是為了讓θ不要過大而加的一個正則項，既然加了正則項那就需要再加一個λ作為超引數來進行調節，而既然λ是超參，那就沒法求（是不是從剛才起就在納悶λ怎麼求），只能通過別的方式給我們只能這樣。

         PS：這裡超參的作用是：在式2這整個損失函式裡，如果λ很大，則λ修飾的那一塊佔得比例就大，反之佔得比例小。

         那超引數λ應該如何取呢？答案是：事先給一個，你拍腦門也好按照經驗也好直接給一個，話說機器學習裡總是說調參調參，調的就是這個參。

         因此在機器學習中，經常這樣分類資料：

         1，如果模型是這樣：

         那就如下圖所示：

         把整個資料集分成兩部分，一部分用於訓練引數θ，一部分用於測試效果。

         2，如果模式是這樣：

         那就如下圖所示：

         從訓練資料中本來用來訓練引數θ那部分中預留一部分用於驗證當前的超引數λ怎麼樣。

         另：機器學習中有個“十折交叉驗證”，感興趣的可以自己去查查。

最後

         還是之前如何求θ的公式：

                   θ= (X^TX)^-1X^Ty

         話說這樣求θ是沒一點問題的，不過在機器學習中習慣使用梯度下降演算法來求θ，這個我已經總結了，這裡就不再寫了。

線性迴歸的程式碼

         這裡data是一個類似下圖這樣的矩陣

                   1  x₀₁  x₀₂  ...  x_0n  y₀

                   1  x₁₁  x₁₂  ...  x_1n  y₁

                   ...

                   1  x_m1  x_m2  ...  x_mn  y_m

         其中，第一列是截距，如下圖所示：

         這裡的1就是箭頭所指的位置，注意：這個和殘差不一樣。

         xij是樣本的特徵，每一行對應一個樣本

         ym是樣本的結果。