prim演算法的java實現
MST(Minimum Spanning Tree,最小生成樹)問題有兩種通用的解法,Prim演算法就是其中之一,它是從點的方面考慮構建一顆MST,大致思想是:設圖G頂點集合為U,首先任意選擇圖G中的一點作為起始點a,將該點加入集合V,再從集合U-V中找到另一點b使得點b到V中任意一點的權值最小,此時將b點也加入集合V;以此類推,現在的集合V={a,b},再從集合U-V中找到另一點c使得點c到V中任意一點的權值最小,此時將c點加入集合V,直至所有頂點全部被加入V,此時就構建出了一顆MST。因為有N個頂點,所以該MST就有N-1條邊,每一次向集合V中加入一個點,就意味著找到一條MST的邊。
用圖示和程式碼說明:
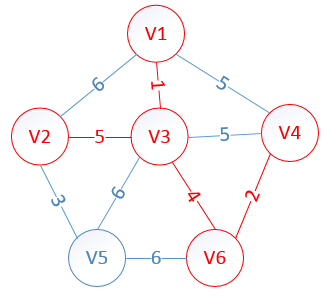
初始狀態:
設定2個資料結構:
lowcost[i]:表示以i為終點的邊的最小權值,當lowcost[i]=0說明以i為終點的邊的最小權值=0,也就是表示i點加入了MST
mst[i]:表示對應lowcost[i]的起點,即說明邊<mst[i],i>是MST的一條邊,當mst[i]=0表示起點i加入MST
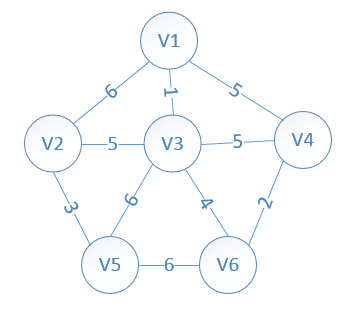
我們假設V1是起始點,進行初始化(*代表無限大,即無通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,
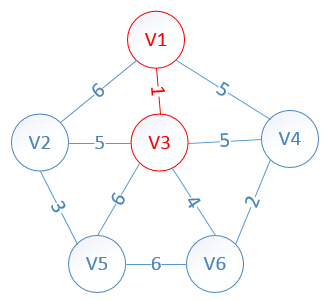
明顯看出,以V3為終點的邊的權值最小=1,所以邊<mst[3],3>=1加入MST
此時,因為點V3的加入,需要更新lowcost陣列和mst陣列:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
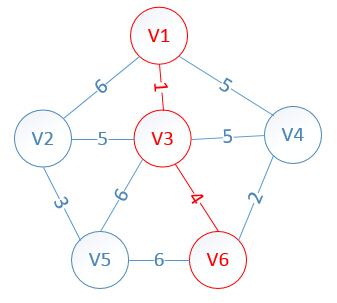
明顯看出,以V6為終點的邊的權值最小=4,所以邊<mst[6],6>=4加入MST
此時,因為點V6的加入,需要更新lowcost陣列和mst陣列:
lowcost[2]=5,
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
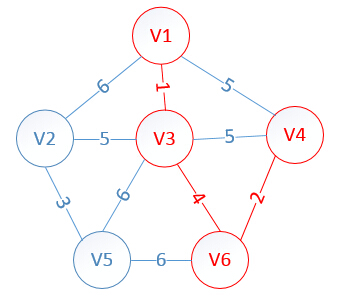
明顯看出,以V4為終點的邊的權值最小=2,所以邊<mst[4],4>=4加入MST
此時,因為點V4的加入,需要更新lowcost陣列和mst陣列:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明顯看出,以V2為終點的邊的權值最小=5,所以邊<mst[2],2>=5加入MST
此時,因為點V2的加入,需要更新lowcost陣列和mst陣列:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明顯,以V5為終點的邊的權值最小=3,所以邊<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
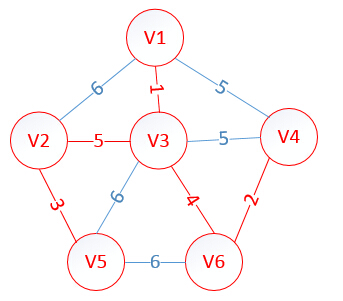
至此,MST構建成功,如圖所示:
package suanfa;
public class Main {
public static void main(String[] args) throws Exception {
int MAX = Integer.MAX_VALUE;
int[][] map = new int[][]{
{0,10,MAX,MAX,MAX,11,MAX,MAX,MAX},
{10,0,18,MAX,MAX,MAX,16,MAX,12},
{MAX,MAX,0,22,MAX,MAX,MAX,MAX,8},
{MAX,MAX,22,0,20,MAX,MAX,16,21},
{MAX,MAX,MAX,20,0,26,MAX,7,MAX},
{11,MAX,MAX,MAX,26,0,17,MAX,MAX},
{MAX,16,MAX,MAX,MAX,17,0,19,MAX},
{MAX,MAX,MAX,16,7,MAX,19,0,MAX},
{MAX,12,8,21,MAX,MAX,MAX,MAX,0}
};
int sum = prim(map);
System.out.println(sum);
}
public static int prim(int[][] arr){
//統計最小的權
int sum = 0;
//當前最小生成樹所能到達的頂點的最小權陣列
int[] costs = new int[9];
//當前各個頂點對應的起點
int[] startPoint = new int[9];
//初始化
for(int i =1;i<9;i++){
//所有點的起點賦值為0
startPoint[i] = 0;
//以0為起點到達各個頂點的權值
costs[i] = arr[0][i];
}
//挑選剩餘的8個頂點
for(int i = 1;i<9;i++){
//記錄當前costs裡面的最小權值是多少
int min = Integer.MAX_VALUE;
//記錄當前costs裡面的最小權值對應的陣列下標,即頂點
//(陣列[頂點]=該頂點對應的起點)
int minIndex = 0;
//遍歷costs
for(int j=1;j<9;j++){
int temp = costs[j];
//costs[j]==0代表節點j已加入MST
if(temp!=0&&temp < min){
min = temp;
minIndex = j;
}
}
sum+=min;
//將已加入MST的對應的權值賦值為0
costs[minIndex] = 0;
//選定了新的頂點到MST後,樹到達各頂點的最小開銷和起點將更新
//更新costs和startPoint
for(int k=0;k<9;k++){
//用minIndex頂點到各個頂點的權值比較costs陣列的值,若較小則替換,並更新起點為minIndex
int newCost = arr[minIndex][k];
if(newCost!=0&&newCost<costs[k]){
costs[k] = newCost;
//更新K的起點為minIndex
startPoint[k] = minIndex;
}
}
}
return sum;
}
}