一、有權圖

之前我們知道，在無權重的圖中，求兩個頂點之間的最短路徑，可以使用 廣度優先搜尋 演算法。但是，當邊存在權重（也可以理解為路程的長度）時，廣度優先搜尋不再適用。 針對有權圖中的兩點間最短路徑，目前主要有 狄克斯特拉演算法 和 貝爾曼福德演算法 兩種解決方法。本部落格以狄克斯特拉演算法為例。

二、狄克斯特拉演算法

1. 簡介

狄克斯特拉（Dijkstra）演算法解決的是帶權重的有向圖上單源最短路徑問題，該演算法有一個限制條件即：所有邊的權重都必須為非負數。如果存在負數邊，則推薦使用貝爾曼福德（Bellman-Ford）演算法。

2. 演算法思想

狄克斯特拉演算法的思想還是貪婪演算法。 首先，我們從起點開始，更新起點到其直接相鄰點的路程距離； 其次，我們在剩餘點中找到離起點最近的一個點，並更新該點所有直接相鄰點到起點的路程距離； 接下來，我們一直重複上一步，始終在剩餘點中找一個距離起點最近的點，並更新其所有鄰居點到起點的距離； 最後，遍歷完所有頂點，完成計算。

3. 圖解過程

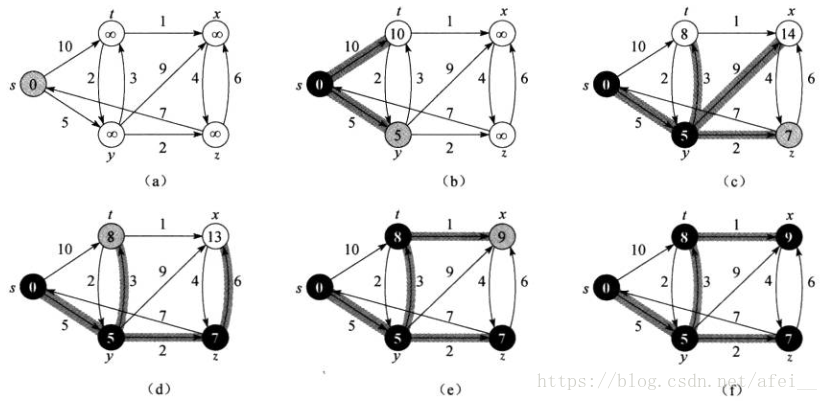
下圖中，起點為 s 點。灰色點表示當前處理的結點，黑色點表示已經處理過的結點，白色點表示未處理的結點。開始時我們設定起點的距離為 0，其餘點均為無窮大（∞）。我們從起點開始，依次更新其鄰居結點到起點的距離，直至完成。帶陰影的邊表示當前最優的路徑。（圖片引用自《演算法導論》一書）

三、程式碼實現

以上圖為例吧，當然我們需要將圖中的元素都抽象為 Java 中的類，即：

1. Vertex 類

大致有四個屬性：

• 第一我們需要知道這個頂點是誰，即頂點的 id；
• 第二我們需要知道這個頂點能到達的鄰居頂點都有哪些，並且還要知道到達鄰居頂點的路程有多長。所以我選擇使用一個 HashMap<Vertext, Integer> 儲存，其鍵為鄰居頂點 Vertex，其值為到達該頂點的路程長度；
• 第三我們想要知道完整路徑是怎樣的話，我們還得知道上一個頂點是誰，即 predecessor；
• 最後，我們儲存一個變數 distance，儲存該頂點離起始點的距離。

import java.util.HashMap;
 
public class Vertex {
 
    private char id; // 頂點的標識
    private HashMap<Vertex, Integer> neighbors; // 當前頂點可直接達到的頂點及其長度(權重)
    private Vertex predecessor; // 上一個頂點是誰(前驅)，用來記錄路徑的
    private
 
 int distance = Integer.MAX_VALUE; // 距離起始點的距離
 
    public Vertex(char id) {
        this.id = id;
        this.neighbors = new HashMap<>();
    }
 
    public char getId() {
        return id;
    }
 
    public HashMap<Vertex, Integer> getNeighbors() {
        return neighbors;
    }
 
    public void addNeighbor(Vertex vertex, int weight) {
        neighbors.put(vertex, weight);
    }
 
    public Vertex getPredecessor() {
        return predecessor;
    }
 
    public void setPredecessor(Vertex predecessor) {
        this.predecessor = predecessor;
    }
 
    public int getDistance() {
        return distance;
    }
 
    public void setDistance(int distance) {
        this.distance = distance;
    }
 
    @Override
    public String toString() {
        return String.format("Vertex[%c]: distance is %d , predecessor is '%s'", id, distance,
                predecessor == null ? "null" : predecessor.id);
    }
 
}

2. 場景類

主要有三個方法：

• dijkstra 方法接收和執行計算
• extractMin 方法從剩餘頂點中找出一個 distance 最小的頂點返回
• relax 意為鬆弛操作，即更新某個頂點所有鄰居點的 distance 值

import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
 
public class Main {
 
    public static void main(String[] args) {
        List<Vertex> list = getTestData();
        dijkstra(list);
        for (int i = 0; i < list.size(); i++) {
            System.out.println(list.get(i).toString());
        }
    }
 
    public static void dijkstra(List<Vertex> list) {
        List<Vertex> copy = new LinkedList<>(); // copy一份出來
        copy.addAll(list);
        while (!copy.isEmpty()) {
            // 每次從 copy 中選取一個距離起始點最近的點
            // 並將這個點從 copy 中移除
            Vertex vertex = extractMin(copy);
            relax(vertex);
        }
    }
 
    public static Vertex extractMin(List<Vertex> list) {
        int index = 0;
        for (int i = 1; i < list.size(); i++) {
            if (list.get(index).getDistance() > list.get(i).getDistance()) {
                index = i;
            }
        }
        return list.remove(index);
    }
 
    public static void relax(Vertex vertex) {
        HashMap<Vertex, Integer> map = vertex.getNeighbors();
        for (Vertex neighbor : map.keySet()) {
            int distance = vertex.getDistance() + map.get(neighbor);
            if (neighbor.getDistance() > distance) {
                neighbor.setDistance(distance);
                neighbor.setPredecessor(vertex);
            }
        }
    }
 
    public static List<Vertex> getTestData() {
        Vertex s = new Vertex('s');
        Vertex t = new Vertex('t');
        Vertex x = new Vertex('x');
        Vertex y = new Vertex('y');
        Vertex z = new Vertex('z');
        s.addNeighbor(t, 10); // s->t : 10
        s.addNeighbor(y, 5); // s->y : 5
        t.addNeighbor(x, 1); // t->x : 1
        t.addNeighbor(y, 2); // t->y : 2
        x.addNeighbor(z, 4); // x->z : 4
        y.addNeighbor(t, 3); // y->t : 3
        y.addNeighbor(x, 9); // y->x : 9
        y.addNeighbor(z, 2); // y->z : 2
        z.addNeighbor(x, 6); // z->x : 6
        z.addNeighbor(s, 7); // z->s : 7
        // 起始點離起始點距離為0
        s.setDistance(0);
        LinkedList<Vertex> list = new LinkedList<>();
        list.add(s);
        list.add(t);
        list.add(x);
        list.add(y);
        list.add(z);
        return list;
    }
 
}

3. 執行結果

Vertex[s]: distance is 0 , predecessor is 'null'
Vertex[t]: distance is 8 , predecessor is 'y'
Vertex[x]: distance is 9 , predecessor is 't'
Vertex[y]: distance is 5 , predecessor is 's'
Vertex[z]: distance is 7 , predecessor is 'y'

對應下圖，結果正確。 例如 x 點，其最短距離為 9，路徑為 x ← t ← y ← s （反過來看）。

4. 繼續優化策略

主要是針對 extractMin 方法的一些改進吧。 上述程式碼是通過遍歷所有剩餘點找出一個最小的 distance。如果我們將剩餘點儲存在一個最小堆實現的優先佇列中，那麼我們只需要直接取出隊首元素即可，並且鬆弛操作更新 distance 時，調整最小堆的操作耗時也只是 log₂ 級別的，頂點數較多時比較適用。 如果，我們使用斐波那契堆實現最小優先佇列，將會更加改善其效率，因為它調整堆的操作攤還代價為 O(1)，而演算法中由於更新 distance 的操作更頻繁所以更適用。不過這個我也沒嘗試過了。 最後，就是第一次執行 extractMin 方法肯定是返回起始點，其實可以少做一次 extractMin 方法。