BP神經網路演算法之matlab具體實現
阿新 • • 發佈:2019-01-28
之前的幾篇部落格的一個共同點就是梯度下降法,梯度下降法是用來求解無約束最優化問題的一個數值方法,簡單實用,幾乎是大部分演算法的基礎,下面來利用梯度下降法優化BP神經網路。
[TOC]
梯度公式
下面的BP神經網路結構為最簡單的三層網路,各層的神經元數量分別為B1,B2,B3。其中X,H,b2,O,b3均為行向量,W12,W23大小分別為(B1,B2)和(B2,B3)
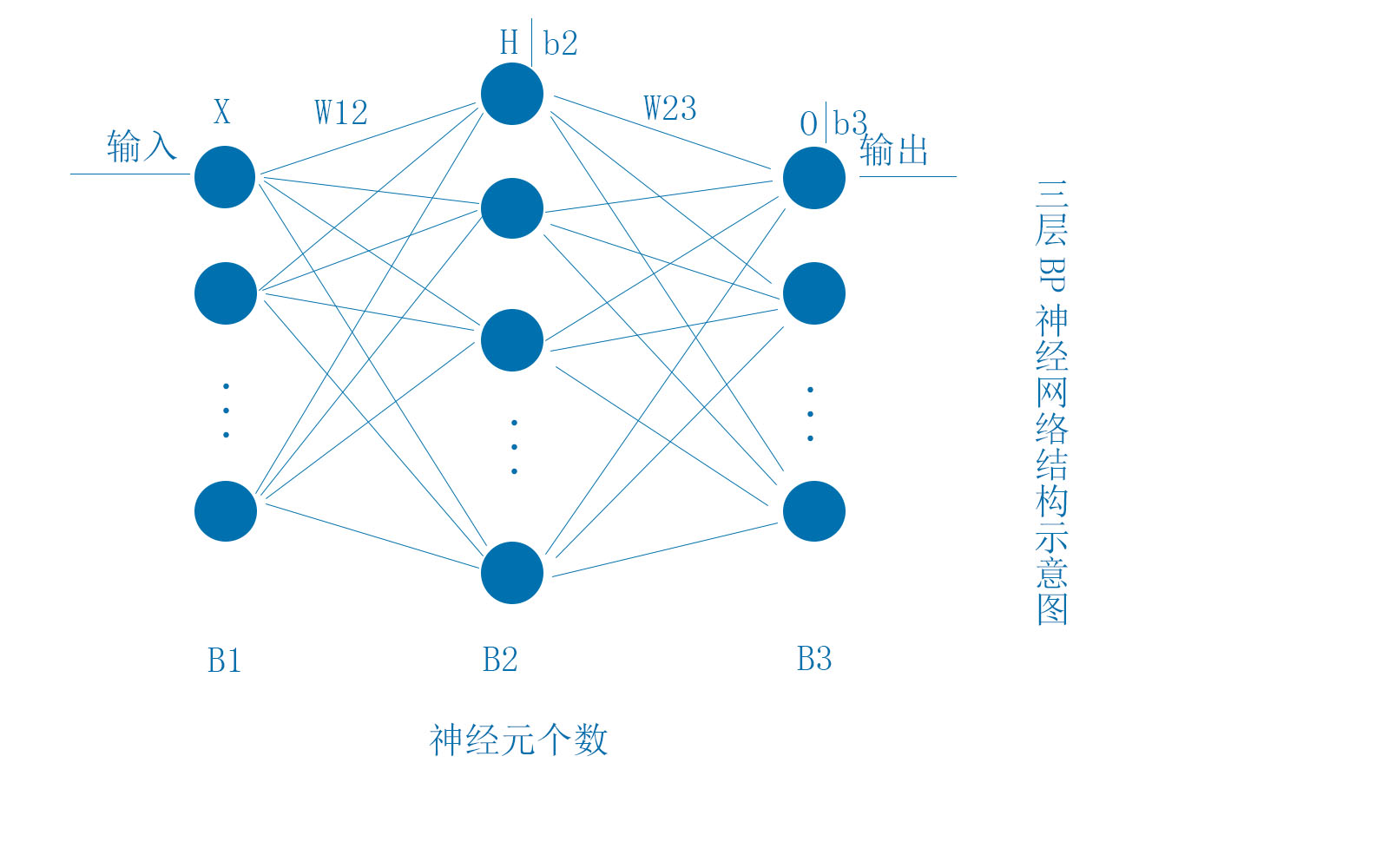
BP神經網路的基本原理,通過輸入X,經過非線性對映到輸出O(樣本大小為m),誤差為:
顯然,我們想要的是J越小越好。
根據上面的網路結構可得H、O的計算公式:
f函式為:
下面採用梯度下降法求解J的最小值時對應的網路的權閾值:
如果資料集較小時,採用上述公式還可以,但是,當資料集特別大時,也就是m很大,那麼梯度的計算將耗費大量時間,所以我們採用單樣本誤差來調整網路的權閾值。即,每使用一個樣本就調整權閾值,那麼J函式的形式更改如下:
J損失函式
權閾值梯度公式
下面就新的J函式來推導梯度公式:
即
