翻譯來源      matble中的help spdiags               

轉載請註明出處https://blog.csdn.net/zhmjunjun/article/details/79790957   謝謝

spdiags函式推廣了斜對角函式的應用，可以進行四種不同的操作，如下：

B = spdiags(A)     從m-by-n矩陣A中提取所有非零對角。B是一個min(m，n)-by-p矩陣，其列是A矩陣的p非零對角

[B,d] = spdiags(A) 返回長度為p的向量d，其整數部分對應A中的對角線（非零對角元素）。

B = spdiags(A,d) 提取d指定的對角線。

A = spdiags(B,d,A)

A = spdiags(B,d,m,n) 通過獲取B的列並將它們放置在d指定的對角線上，建立一個m-by-n稀疏矩陣。.

A：  m-by-n矩陣，通常(但不一定)稀疏，其非零或指定元素位於p對角上.

B：  最小(m，n)-by-p矩陣，p為矩陣A非零斜對角線條數。

d：  長度為p的向量，是每一條非零斜對角線對應的計數標，，所以向量d的長度為p，因為矩陣A有p條非零斜對角。

Roughly, A, B, and d are related by

for k = 1:p
    B(:,k) = diag(A,d(k))
end

m-by-n 的矩陣A具有m+n-1個對角.它們是在向量d中使用從-m+1到n-1的索引指定的。

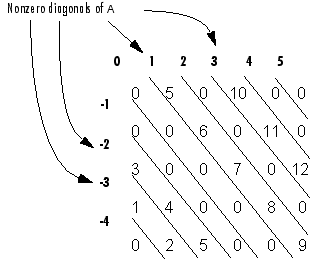
A為5X6的矩陣，矩陣A對應10個對角，分別用-4，-3，……，4，5標記。

如下圖：

例項列舉幫助理解——————————————————————————————————

A=[0 5 0 10 0 0;...
0 0 6 0 11 0;...
3 0 0 7 0 12;...
1 4 0 0 8 0;...
0 2 5 0 0 9]

[B, d]  =spdiags(A)

%%min（size（A））=5;   因此5為B矩陣的列，非零斜對角為B矩陣的行，

%%因為size（A）將輸出矩陣A的  行 與 列，這裡分別是5  與  6。    因此  min（size（A））=5

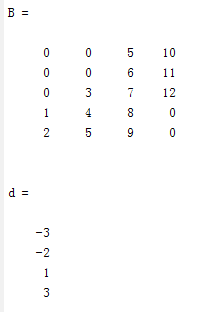
第一個輸出B的列包含A的非零對角，第二個輸出d列出A的非零對角的索引，如下圖所示

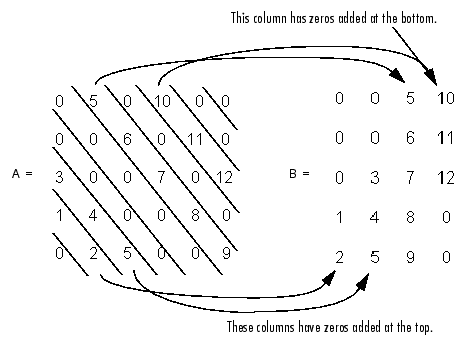
請注意，A中最長的非零對角線包含在B的第3列中，A的其他非零對角線在B中相應的列中添加了額外的零，使B的所有列都具有相同的長度。對於A的主對角線以下的非零對角線，在列的頂部加上額外的零。對於A的主對角線以上的非零對角線，在列的底部加上額外的零。下圖說明了這一點。

例二：此示例生成n點上經典的第二差分運算元的稀疏三對角表示。（這個例子不好看出相互關係，但下一個例子可以看出一些）

e = ones(n,1);
A = spdiags([e -2*e e], -1:1, n, n)
%Turn it into Wilkinson's test matrix (see gallery):

A = spdiags(abs(-(n-1)/2:(n-1)/2)',0,A)
%Finally, recover the three diagonals:

B = spdiags(A)

執行程式碼時，將n具體化

 例三     

A = [11    0   13    0
      0   22    0   24
      0    0   33    0
     41    0    0   44
      0   52    0    0
      0    0   63    0
      0    0    0   74]
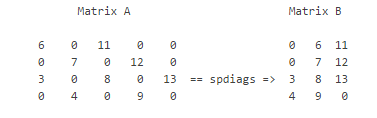
%   Here m =7, n = 4, and p = 3.  p為非零斜對角線條數

[B,d] = spdiags(A)    

 d = [-3 0 2]' 
B = [41   11    0
     52   22    0
     63   33   13
     74   44   24]

相反，對於上面的B和d，表示式spdiags(B,d,7,4)複製了原始的A。

為什麼是7,4？因為想要還原的 原始矩陣A（為4X7的矩陣）

>> spdiags(B,d,7,4)
%    d是對應的非零斜對角的位置； 7,4.為構建一個列為7，行為4的矩陣，除了將矩陣B的元素，按照d非零斜對角線的位置還原，其餘都填補0；

%    結果為，這些正好對應於原始矩陣A的相應位置，按A矩陣的列表示。（因為A矩陣正好是列為7，行為4的矩陣）
ans =
   (1,1)       11
   (4,1)       41
   (2,2)       22
   (5,2)       52
   (1,3)       13
   (3,3)       33
   (6,3)       63
   (2,4)       24
   (4,4)       44
   (7,4)       74

例四 此示例演示了當B列 比要替換的對角線長時；spdiags如何建立對角線。(方法一樣，就是將多餘部分刪除，負數順序，正數倒序錄入，，自己畫一下就一下子理解了)    ，repmat（A，n，m）函式主要功能是，矩陣塊的複製。將矩陣A當做塊，填充矩陣nXm。  具體可以在matble中，輸入：    help repmat

B = repmat((1:6)',[1 7])

B =

    1  1  1  1  1  1  1
    2  2  2  2  2  2  2
    3  3  3  3  3  3  3
    4  4  4  4  4  4  4
    5  5  5  5  5  5  5
    6  6  6  6  6  6  6

d = [-4 -2 -1 0 3 4 5];
A = spdiags(B,d,6,6);
full(A)

ans =

  1  0  0  4  5  6
  1  2  0  0  5  6
  1  2  3  0  0  6
  0  2  3  4  0  0
  1  0  3  4  5  0
  0  2  0  4  5  6

三個圖例，將A=spdiags（B,d,n,m）的所以轉化情況都給出了，

當A矩陣行<=列時，下對角順序；上對角逆序

當A矩陣行>列時，下對角逆序；上對角順序

三個圖例將    B = spdiags(A) 的所有情況表示出來

當A矩陣行<=列時，下對角順序；上對角逆序

當A矩陣行>列時，下對角逆序；上對角順序