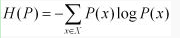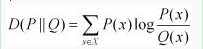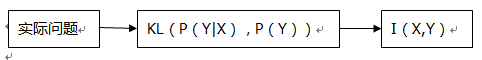【轉】：http://m.blog.csdn.net/blog/ice110956/17120461

同： http://www.huangwc.cn/

資訊度量

資訊理論中，把資訊大小解釋為其不確定度。如果一個事件必然發生，那麼他沒有不確定度，也就不包含資訊。即資訊=不確定度。

借用數學之美中的一個例子：

馬上要舉行世界盃賽了。大家都很關心誰會是冠軍。假如我錯過了看世界盃，賽後我問一個知道比賽結果的觀眾“哪支球隊是冠軍”？ 他不願意直接告訴我， 而要讓我猜，並且我每猜一次，他要收一元錢才肯告訴我是否猜對了，那麼我需要付給他多少錢才能知道誰是冠軍呢? 我可以把球隊編上號，從 1 到 32， 然後提問： “冠軍的球隊在 1-16 號中嗎?” 假如他告訴我猜對了， 我會接著問： “冠軍在 1-8 號中嗎?” 假如他告訴我猜錯了， 我自然知道冠軍隊在 9-16 中。這樣只需要五次， 我就能知道哪支球隊是冠軍。所以，誰是世界盃冠軍這條訊息的資訊量只值五塊錢。 

如果我們再考慮不同球隊獲勝的不同比例，如巴西比例高，中國比例低些，那麼結果又會不同。

互資訊，聯合熵，條件熵的相關定義

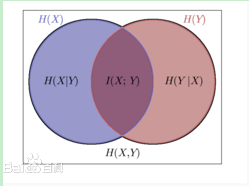
這樣一幅圖：

兩個隨機變數，X，Y。

H（X）表示其資訊量，也就是自資訊

H（X|Y）表示已知Y的情況下X的資訊量，同理，H（Y|X）也是。

H（X，Y）表示X，Y的聯合熵，也就是這兩個變數聯合表示的資訊量。

H（X；Y），也就是I（X；Y），也就是互資訊,指的是兩個變數重複的部分。

H（X；Y）=H（X,Y）- H（X|Y）- H（Y|X）,這個等式從上圖也能形象地看出。

KL距離

KL距離用來度量兩個分佈的相似度。

物理意義：

另一種理解就是，已知Q的分佈，用Q分佈近似估計P，P的不確定度減少了多少。

我們用D（P||Q）表示KL距離，計算公式如下：

也就是用一個分佈來表徵另一個分佈的額外不確定度。

P（X）=Q（X），他們的KL距離為0；否則，差異越大，距離越大。

上述KL距離物理意義的表述，在許多運用中都有很好地體現。

事例：

南京的天氣為隨機變數D，某個南京的同學的穿著W。我想通過W，瞭解D。也就是用P（D/W）來近似P（D），現在定量地計算我們通過穿著，瞭解了多少關於天氣的資訊。

也就是用P（D/W）來代替P（D）編碼，減少了多少不確定度？

用KL距離來表徵，就是：D（P（D/W）||P（D））。

接著，如果已知一個穿著wi,可以選擇最大KL距離D（P（dj/wi）||P（dj））的dj，也就是最可能的天氣。

這就是KL距離的物理意義在實際中的一些運用。

互資訊與KL距離

插入一個概念：獨立與相關。

概率中的相關概念指的是線性相關，而是否獨立，則取決於線性以及非線性的關係。

區別：

X，Y的互資訊I（X,Y）表徵其獨立程度，KL距離表徵其線性相關性。如下圖：

聯絡：

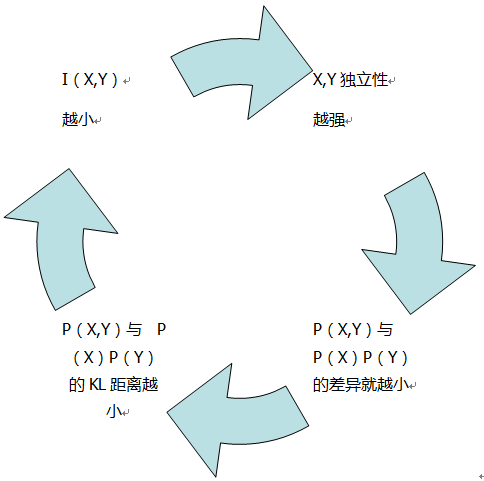
X，Y的互資訊也就是P（X,Y）與P（X）P(Y)的KL距離。

下面這幅圖描繪他們之間的聯絡：

還有下面這個公式：

這個等式描繪了上面舉的天氣和穿著的例子，用P（Y|X）來代替P（Y），不確定度減少了多少？其關於X求和後就是X，Y的互資訊。

上式也是許多運用中常見的等式：

我們可以通過互資訊與KL距離的這種關係，構造一定的互資訊，從而處理一些實際問題。

皮爾森相關係數與KL距離：

聯絡：皮爾森相關係數衡量X,Y的線性相關性。這與KL距離類似。

區別：

比較明顯的區別就是，KL距離是不對等的度量距離，而皮爾森相關係數是對等的度量距離。

實際運用：

如上面天氣與穿著的例子，以及KL距離與互資訊的相互關係。一般運用這些知識，在資訊檢索，自然語言處理方面都有相關運用。