編寫帶有下列宣告的例程：

public void permute(String str);
private void permute(char[] str, int low, int high);

第一個例程是個驅動程式，它呼叫第二個例程並顯示String str中的字元的所有排列。例如，str是"abc"， 那麼輸出的串則是abc，acb，bac，bca，cab，cba，第二個例程使用遞迴。

這題主要使用到遞迴，遞迴的四條基本法則（資料結構與演算法分析-Java語言描述page7）:
1、基準情形。必須總要有某些基準情形，無需遞迴就能解出。
2、不斷推進。對於那些需要遞迴求解的情形，每一次遞迴呼叫都必須要使狀況朝向一種基準情形推進。
3、設計法則

對於字串的排列問題：
如果能生成n-1個元素的全排列，就能生成n個元素的全排列。對於只有一個元素的集合，可以直接生成全排列。所以全排列的遞迴終止條件很明確，只有一個元素時。我們可以分析一下全排列的過程：
(1) 首先，我們固定第一個字元a，求後面兩個字元bc的排列。
(2) 當兩個字元bc排列求好之後，我們把第一個字元a和後面的b交換，得到bac，接著我們固定第一個字元b，求後面兩個字元ac的排列。
(3) 現在是把c放在第一個位置的時候了，但是記住前面我們已經把原先的第一個字元a和後面的b做了交換，為了保證這次c仍是和原先處在第一個位置的a交換，我們在拿c和第一個字元交換之前，先要把b和a交換回來。在交換b和a之後，再拿c和處於第一位置的a進行交換，得到cba。我們再次固定第一個字元c，求後面兩個字元b、a的排列。
(4) 既然我們已經知道怎麼求三個字元的排列，那麼固定第一個字元之後求後面兩個字元的排列，就是典型的遞迴思路了。

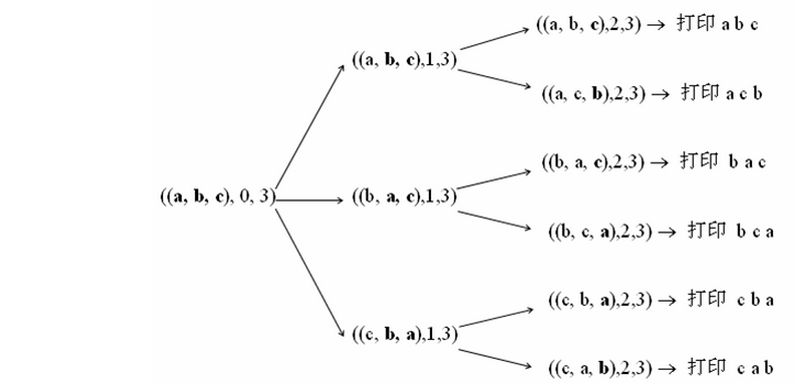
下面這張圖很清楚的給出了遞迴的過程：

public static void permute(String str){
    char[] ch = str.toCharArray();
    permute(ch, 0, ch.length-1);
}

private static void permute(char[] str, int low, int high){
    int length = str.length;
    if(low == high){
        String s = "";
        for(int i=0;i<length;i++){
            s += str
 
[i];
        }
        System.out.println(s);
    }
    for(int i=low; i<length;i++){
        swap(str, i, low);
        permute(str, low+1, high);
        swap(str, i, low);
    }
}

public static void swap(char[] str, int m, int n){
    char temp = str[m];
    str[m] = str[n];
    str[n] = temp;
}

由於全排列就是從第一個數字起，每個數分別與它後面的數字交換，我們先嚐試加個這樣的判斷——如果一個數與後面的數字相同那麼這兩個數就不交換了。例如abb，第一個數與後面兩個數交換得bab，bba。然後abb中第二個數和第三個數相同，就不用交換了。但是對bab，第二個數和第三個數不同，則需要交換，得到bba。由於這裡的bba和開始第一個數與第三個數交換的結果相同了，因此這個方法不行。

換種思維，對abb，第一個數a與第二個數b交換得到bab，然後考慮第一個數與第三個數交換，此時由於第三個數等於第二個數，所以第一個數就不再用與第三個數交換了。再考慮bab，它的第二個數與第三個數交換可以解決bba。此時全排列生成完畢！

這樣，我們得到在全排列中去掉重複的規則：
去重的全排列就是從第一個數字起，每個數分別與它後面非重複出現的數字交換。
在原始碼中加入如下改進程式碼：

for(int i=low; i<length;i++){
    if(is_swap(str, low, i) == 1){
        swap(str, low, i);
        permute(str, low+1, high);
        swap(str, low, i);
    }
}

其中is_swap(char[] str, int m, int n)函式如下。

public static int is_swap(char[] str, int m, int n){
    int flag = 1;
    for(int i=m;i<n;i++){
        flag = 1;
        if(str[i] == str[n]){
            flag = 0;
            break;
        }
    }

    return flag;
}

至此該問題得到解決。