雜湊、HashMap原理及原始碼、Hash的一些應用面試題
阿新 • • 發佈:2019-01-28
一、雜湊定義
Hash,一般翻譯做“雜湊”,也有直接音譯為"雜湊"的,就是把任意長度的輸入(又叫做預對映, pre-image),通過雜湊演算法,變換成固定長度的輸出,該輸出就是雜湊值。這種轉換是一種壓縮對映,也就是,雜湊值的空間通常遠小於輸入的空間,不 同的輸入可能會雜湊成相同的輸出,而不可能從雜湊值來唯一的確定輸入值。
數學表述為:h = H(M) ,其中H( )--單向雜湊函式,M--任意長度明文,h--固定長度雜湊值。
二、基本概念
1、若結構中存在和關鍵字K相等的記錄,則必定在f(K)的儲存位置上。由此,不需比較便可直接取得所查記錄。稱這個對應關係f為雜湊函式(Hash function),按這個思想建立的表為散列表。
對不同的關鍵字可能得到同一雜湊地址,即key1≠key2,而f(key1)=f(key2),這種現象稱衝突。具有相同函式值的關鍵字對該雜湊函式來說稱做同義詞。綜上所述,根據雜湊函式H(key)和處理衝2、突的方法將一組關鍵字映象到一個有限的連續的地址集(區間)上,並以關鍵字在地址集中的“象” 作為記錄在表中的儲存位置,這種表便稱為散列表,這一映象過程稱為雜湊造表或雜湊,所得的儲存位置稱雜湊地址。
3、若對於關鍵字集合中的任一個關鍵字,經雜湊函式映象到地址集合中任何一個地址的概率是相等的,則稱此類雜湊函式為均勻雜湊函式(Uniform Hash function),這就是使關鍵字經過雜湊函式得到一個“隨機的地址”,從而減少衝突。
三、常用的構造雜湊函式的方法
雜湊函式能使對一個數據序列的訪問過程更加迅速有效,通過雜湊函式,資料元素將被更快地定位ǐ
1. 直接定址法:取關鍵字或關鍵字的某個線性函式值為雜湊地址。即H(key)=key或H(key) = a·key + b,其中a和b為常數(這種雜湊函式叫做自身函式)
2. 數字分析法
3. 平方取中法
4. 摺疊法
5. 隨機數法
6. 除留餘數法:取關鍵字被某個不大於散列表表長m的數p除後所得的餘數為雜湊地址。即 H(key) = key MOD p, p<=m。不僅可以對關鍵字直接取模,也可在摺疊、平方取中等運算之後取模。對p的選擇很重要,一般取素數或m,若p選的不好,容易產生同義詞。
四、處理衝突的方法
1. 開放定址法;Hi=(H(key) + di) MOD m, i=1,2,…, k(k<=m-1),其中H(key)為雜湊函式,m為散列表長,di為增量序列,可有下列三種取法:
1. di=1,2,3,…, m-1,稱線性探測再雜湊;
2. di=1^2, (-1)^2, 2^2,(-2)^2, (3)^2, …, ±(k)^2,(k<=m/2)稱二次探測再雜湊;
3. di=偽隨機數序列,稱偽隨機探測再雜湊。 ==
2. 再雜湊法:Hi=RHi(key), i=1,2,…,k RHi均是不同的雜湊函式,即在同義詞產生地址衝突時計算另一個雜湊函式地址,直到衝突不再發生,這種方法不易產生“聚集”,但增加了計算時間。
3. 鏈地址法(拉鍊法)
4. 建立一個公共溢位區
五、Hash演算法的時間複雜度
無衝突的hash table複雜度是O(1),一般是O(c),c為雜湊關鍵字衝突時查詢的平均長度,最壞情況仍然是O(N)。
六、HashMap
1、一個物件當HashMap的key時,必須覆蓋hashCode()和equals()方法,hashCode()的返回值儘可能的分散。
2、當HashMap的entry的陣列足夠大,key的hash值足夠分散時,即是可以實現一個entry陣列下標最多隻對應了一個entry,此時get方法的時間複雜度可以達到O(1)。
3、在陣列長度和get方法的速度上要達到一個平衡。陣列比較長碰撞出現的概率就比較小,所以get方法獲取值時就比較快,但浪費了比較多的空間;當陣列長度沒有冗餘時,碰撞出現的概率比較大,雖然節省了空間,但會犧牲get方法的時間。
4、HashMap有預設的裝載因子loadFactor=0.75,預設的entry陣列的長度為16。裝載因子的意義在於使得entry陣列有冗餘,預設即允許25%的冗餘,當HashMap的資料的個數超過12(16*0.75)時即會對entry陣列進行第一次擴容,後面的再次擴容依次類推。
5、HashMap每次擴容一倍,resize時會將已存在的值從新進行陣列下標的計算,這個是比較浪費時間的。在平時使用中,如果能估計出大概的HashMap的容量,可以合理的設定裝載因子loadFactor和entry陣列初始長度即可以避免resize操作,提高put的效率。
1、map是一種key、value形式的鍵值對,將hash表和map結合即形成了HashMap。
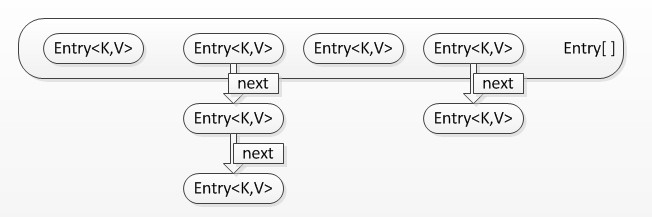
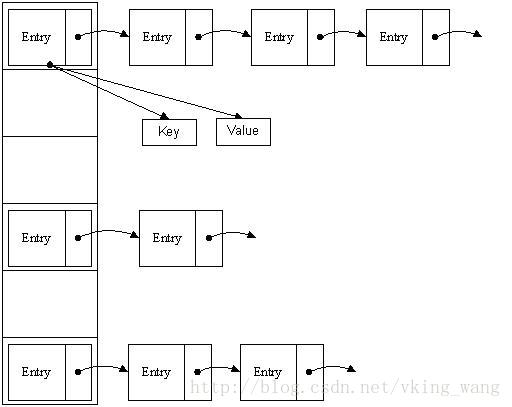
2、Java中HashMap的資料是以Entry陣列的形式存放的,HashMap通過對key進行hash運算得到一個數組下標,然後將資料存放到Entry陣列對應的位置,又因為不同的key進行hash運算可能會得到一個相同的陣列下標,為了解決碰撞覆蓋衝突,所以Entry本身又是一個連結串列的結構,即以後不同的key相同陣列下標的資料的next會被賦值為已存在Entry連結串列,新的Entry會替換陣列值。
3、HashMap的儲存資料的示例圖如下:
(1)對key的hashcode進行hash計算,獲取應該儲存到陣列中的index。
(2)判斷index所指向的陣列元素是否為空,如果為空則直接插入。
(3)如果不為空,則依次查詢entry中next所指定的元素,判讀key是否相等,如果相等,則替換久的值,返回。
(4)如果都不相等,則將此連結串列頭元素賦值給待插入entry的next變數,讓後將待插入元素插入到entry陣列中去。
(5)當然HashMap裡面也包含一些優化方面的實現,這裡也說一下。比如:Entry[]的長度一定後,隨著map裡面資料的越來越長,這樣同一個index的鏈就會很長,會不會影響效能?HashMap裡面設定一個因子,隨著map的size越來越大,Entry[]會以一定的規則加長長度。
6、確定陣列index:hashcode % table.length取模
按位取並,作用上相當於取模mod或者取餘%。這意味著陣列下標相同,並不表示hashCode相同。
7、解決hash衝突的辦法
開放定址法(線性探測再雜湊,二次探測再雜湊,偽隨機探測再雜湊)
再雜湊法
鏈地址法
建立一個公共溢位區
Java中hashmap的解決辦法就是採用的鏈地址法。
8、再雜湊rehash過程
當雜湊表的容量超過預設容量時,必須調整table的大小。當容量已經達到最大可能值時,那麼該方法就將容量調整到Integer.MAX_VALUE返回,這時,需要建立一張新表,將原表的對映到新表中。
八、Hash應用例子
搜尋引擎會通過日誌檔案把使用者每次檢索使用的所有檢索串都記錄下來,每個查詢串的長度為1-255位元組。假設目前有一千萬個記錄(這些查詢串的重複度比較高,雖然總數是1千萬,但如果除去重複後,不超過3百萬個。一個查詢串的重複度越高,說明查詢它的使用者越多,也就是越熱門。),請你統計最熱門的10個查詢串,要求使用的記憶體不能超過1G。
第一步:Query統計
1、直接排序法
首先我們最先想到的的演算法就是排序了,首先對這個日誌裡面的所有Query都進行排序,然後再遍歷排好序的Query,統計每個Query出現的次數了。
但是題目中有明確要求,那就是記憶體不能超過1G,一千萬條記錄,每條記錄是255Byte,很顯然要佔據2.375G記憶體,這個條件就不滿足要求了。
讓我們回憶一下資料結構課程上的內容,當資料量比較大而且記憶體無法裝下的時候,我們可以採用外排序的方法來進行排序,這裡我們可以採用歸併排序,因為歸併排序有一個比較好的時間複雜度O(nlogn)。
排完序之後我們再對已經有序的Query檔案進行遍歷,統計每個Query出現的次數,再次寫入檔案中。
綜合分析一下,排序的時間複雜度是O(nlogn),而遍歷的時間複雜度是O(n),因此該演算法的總體時間複雜度就是O(n+nlogn)=O(nlogn)。
2、Hash Table法
在第1個方法中,我們採用了排序的辦法來統計每個Query出現的次數,時間複雜度是O(nlogn),那麼能不能有更好的方法來儲存,而時間複雜度更低呢?
題目中說明了,雖然有一千萬個Query,但是由於重複度比較高,因此事實上只有300萬的Query,每個Query 255Byte,因此我們可以考慮把他們都放進記憶體中去,而現在只是需要一個合適的資料結構,在這裡,Hash Table絕對是我們優先的選擇,因為Hash Table的查詢速度非常的快,幾乎是O(1)的時間複雜度。
那麼,我們的演算法就有了:維護一個Key為Query字串,Value為該Query出現次數的HashTable,每次讀取一個Query,如果該字串不在Table中,那麼加入該字串,並且將Value值設為1;如果該字串在Table中,那麼將該字串的計數加一即可。最終我們在O(n)的時間複雜度內完成了對該海量資料的處理。
本方法相比演算法1:在時間複雜度上提高了一個數量級,為O(n),但不僅僅是時間複雜度上的優化,該方法只需要IO資料檔案一次,而演算法1的IO次數較多的,因此該演算法2比演算法1在工程上有更好的可操作性。
第二步:找出Top 10
演算法一:普通排序
我想對於排序演算法大家都已經不陌生了,這裡不在贅述,我們要注意的是排序演算法的時間複雜度是O(nlogn),在本題目中,三百萬條記錄,用1G記憶體是可以存下的。
演算法二:部分排序
題目要求是求出Top 10,因此我們沒有必要對所有的Query都進行排序,我們只需要維護一個10個大小的陣列,初始化放入10個Query,按照每個Query的統計次數由大到小排序,然後遍歷這300萬條記錄,每讀一條記錄就和陣列最後一個Query對比,如果小於這個Query,那麼繼續遍歷,否則,將陣列中最後一條資料淘汰,加入當前的Query。最後當所有的資料都遍歷完畢之後,那麼這個陣列中的10個Query便是我們要找的Top10了。
不難分析出,這樣,演算法的最壞時間複雜度是N*K, 其中K是指top多少。
演算法三:堆
在演算法二中,我們已經將時間複雜度由NlogN優化到NK,不得不說這是一個比較大的改進了,可是有沒有更好的辦法呢?
分析一下,在演算法二中,每次比較完成之後,需要的操作複雜度都是K,因為要把元素插入到一個線性表之中,而且採用的是順序比較。這裡我們注意一下,該陣列是有序的,一次我們每次查詢的時候可以採用二分的方法查詢,這樣操作的複雜度就降到了logK,可是,隨之而來的問題就是資料移動,因為移動資料次數增多了。不過,這個演算法還是比演算法二有了改進。
基於以上的分析,我們想想,有沒有一種既能快速查詢,又能快速移動元素的資料結構呢?回答是肯定的,那就是堆。
藉助堆結構,我們可以在log量級的時間內查詢和調整/移動。因此到這裡,我們的演算法可以改進為這樣,維護一個K(該題目中是10)大小的小根堆,然後遍歷300萬的Query,分別和根元素進行對比。
思想與上述演算法二一致,只是演算法在演算法三,我們採用了最小堆這種資料結構代替陣列,把查詢目標元素的時間複雜度有O(K)降到了O(logK)。
那麼這樣,採用堆資料結構,演算法三,最終的時間複雜度就降到了N‘logK,和演算法二相比,又有了比較大的改進。
總結:
至此,演算法就完全結束了,經過上述第一步、先用Hash表統計每個Query出現的次數,O(N);然後第二步、採用堆資料結構找出Top 10,N*O(logK)。所以,我們最終的時間複雜度是:O(N)+N'*O(logK)。(N為1000萬,N’為300萬)。如果各位有什麼更好的演算法,歡迎留言評論。
九、參考:
http://www.cnblogs.com/wangjy/archive/2011/09/08/2171638.html
Java集合類之HashMap原始碼分析: http://www.open-open.com/lib/view/open1363245226500.html#
http://kb.cnblogs.com/page/189480/
Hash,一般翻譯做“雜湊”,也有直接音譯為"雜湊"的,就是把任意長度的輸入(又叫做預對映, pre-image),通過雜湊演算法,變換成固定長度的輸出,該輸出就是雜湊值。這種轉換是一種壓縮對映,也就是,雜湊值的空間通常遠小於輸入的空間,不 同的輸入可能會雜湊成相同的輸出,而不可能從雜湊值來唯一的確定輸入值。
數學表述為:h = H(M) ,其中H( )--單向雜湊函式,M--任意長度明文,h--固定長度雜湊值。
二、基本概念
1、若結構中存在和關鍵字K相等的記錄,則必定在f(K)的儲存位置上。由此,不需比較便可直接取得所查記錄。稱這個對應關係f為雜湊函式(Hash function),按這個思想建立的表為散列表。
對不同的關鍵字可能得到同一雜湊地址,即key1≠key2,而f(key1)=f(key2),這種現象稱衝突。具有相同函式值的關鍵字對該雜湊函式來說稱做同義詞。綜上所述,根據雜湊函式H(key)和處理衝2、突的方法將一組關鍵字映象到一個有限的連續的地址集(區間)上,並以關鍵字在地址集中的“象” 作為記錄在表中的儲存位置,這種表便稱為散列表,這一映象過程稱為雜湊造表或雜湊,所得的儲存位置稱雜湊地址。
3、若對於關鍵字集合中的任一個關鍵字,經雜湊函式映象到地址集合中任何一個地址的概率是相等的,則稱此類雜湊函式為均勻雜湊函式(Uniform Hash function),這就是使關鍵字經過雜湊函式得到一個“隨機的地址”,從而減少衝突。
三、常用的構造雜湊函式的方法
雜湊函式能使對一個數據序列的訪問過程更加迅速有效,通過雜湊函式,資料元素將被更快地定位ǐ
1. 直接定址法:取關鍵字或關鍵字的某個線性函式值為雜湊地址。即H(key)=key或H(key) = a·key + b,其中a和b為常數(這種雜湊函式叫做自身函式)
2. 數字分析法
3. 平方取中法
4. 摺疊法
5. 隨機數法
6. 除留餘數法:取關鍵字被某個不大於散列表表長m的數p除後所得的餘數為雜湊地址。即 H(key) = key MOD p, p<=m。不僅可以對關鍵字直接取模,也可在摺疊、平方取中等運算之後取模。對p的選擇很重要,一般取素數或m,若p選的不好,容易產生同義詞。
四、處理衝突的方法
1. 開放定址法;Hi=(H(key) + di) MOD m, i=1,2,…, k(k<=m-1),其中H(key)為雜湊函式,m為散列表長,di為增量序列,可有下列三種取法:
1. di=1,2,3,…, m-1,稱線性探測再雜湊;
2. di=1^2, (-1)^2, 2^2,(-2)^2, (3)^2, …, ±(k)^2,(k<=m/2)稱二次探測再雜湊;
3. di=偽隨機數序列,稱偽隨機探測再雜湊。 ==
2. 再雜湊法:Hi=RHi(key), i=1,2,…,k RHi均是不同的雜湊函式,即在同義詞產生地址衝突時計算另一個雜湊函式地址,直到衝突不再發生,這種方法不易產生“聚集”,但增加了計算時間。
3. 鏈地址法(拉鍊法)
4. 建立一個公共溢位區
五、Hash演算法的時間複雜度
無衝突的hash table複雜度是O(1),一般是O(c),c為雜湊關鍵字衝突時查詢的平均長度,最壞情況仍然是O(N)。
六、HashMap
1、一個物件當HashMap的key時,必須覆蓋hashCode()和equals()方法,hashCode()的返回值儘可能的分散。
2、當HashMap的entry的陣列足夠大,key的hash值足夠分散時,即是可以實現一個entry陣列下標最多隻對應了一個entry,此時get方法的時間複雜度可以達到O(1)。
3、在陣列長度和get方法的速度上要達到一個平衡。陣列比較長碰撞出現的概率就比較小,所以get方法獲取值時就比較快,但浪費了比較多的空間;當陣列長度沒有冗餘時,碰撞出現的概率比較大,雖然節省了空間,但會犧牲get方法的時間。
4、HashMap有預設的裝載因子loadFactor=0.75,預設的entry陣列的長度為16。裝載因子的意義在於使得entry陣列有冗餘,預設即允許25%的冗餘,當HashMap的資料的個數超過12(16*0.75)時即會對entry陣列進行第一次擴容,後面的再次擴容依次類推。
5、HashMap每次擴容一倍,resize時會將已存在的值從新進行陣列下標的計算,這個是比較浪費時間的。在平時使用中,如果能估計出大概的HashMap的容量,可以合理的設定裝載因子loadFactor和entry陣列初始長度即可以避免resize操作,提高put的效率。
6、HashMap不是執行緒安全的,多執行緒環境下可以使用Hashtable或ConcurrentHashMap。
7、我們能否讓HashMap同步?
HashMap可以通過下面的語句進行同步:
Map m = Collections.synchronizeMap(hashMap);
1、map是一種key、value形式的鍵值對,將hash表和map結合即形成了HashMap。
2、Java中HashMap的資料是以Entry陣列的形式存放的,HashMap通過對key進行hash運算得到一個數組下標,然後將資料存放到Entry陣列對應的位置,又因為不同的key進行hash運算可能會得到一個相同的陣列下標,為了解決碰撞覆蓋衝突,所以Entry本身又是一個連結串列的結構,即以後不同的key相同陣列下標的資料的next會被賦值為已存在Entry連結串列,新的Entry會替換陣列值。
3、HashMap的儲存資料的示例圖如下:
圖1:
圖2:
public V put(K key, V value) {
if (table == EMPTY_TABLE) {
inflateTable(threshold);
}
if (key == null)
return putForNullKey(value);// HashMap接收key為null的資料
int hash = hash(key);//對key的hashCode再進行hash運算
int i = indexFor(hash, table.length);//根據hash值和entry陣列的大小計算出新增資料應該存放的陣列位置
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
// for迴圈遍歷找到的陣列下標的entry,如果hash值和key都相等,則覆蓋原來的value值
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
//如果上面for迴圈沒有找到相同的hash和key,則增加一個entry
addEntry(hash, key, value, i);
return null;
}
void addEntry(int hash, K key, V value, int bucketIndex) {
if ((size >= threshold) && (null != table[bucketIndex])) {
resize(2 * table.length); //如果size超過threshold,則擴充table大小。再雜湊
hash = (null != key) ? hash(key) : 0;
bucketIndex = indexFor(hash, table.length);
}
createEntry(hash, key, value, bucketIndex);
}
void createEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
//new 一個新的entry,賦值給當前下標陣列
table[bucketIndex] = new Entry<>(hash, key, value, e); //引數e, 是Entry.next
size++;
}
Entry(int h, K k, V v, Entry<K,V> n) {
value = v;
//在HashMap的Entry中有四個變數,key、value、hash、next,其中next用於在hash方法新增值衝突時候,所指向的下一個值。
next = n;//即將原來陣列下標對應的entry賦值給新的entry的next
key = k;
hash = h;
}(1)對key的hashcode進行hash計算,獲取應該儲存到陣列中的index。
(2)判斷index所指向的陣列元素是否為空,如果為空則直接插入。
(3)如果不為空,則依次查詢entry中next所指定的元素,判讀key是否相等,如果相等,則替換久的值,返回。
(4)如果都不相等,則將此連結串列頭元素賦值給待插入entry的next變數,讓後將待插入元素插入到entry陣列中去。
(5)當然HashMap裡面也包含一些優化方面的實現,這裡也說一下。比如:Entry[]的長度一定後,隨著map裡面資料的越來越長,這樣同一個index的鏈就會很長,會不會影響效能?HashMap裡面設定一個因子,隨著map的size越來越大,Entry[]會以一定的規則加長長度。
PS: HashMap,也是先判斷hashcode(hashcode相同,所以它們的table位置相同,‘碰撞’會發生。因為HashMap使用連結串列儲存物件,這個Entry(包含有鍵值對的Map.Entry物件)會儲存在連結串列中。),再判斷equals,如果都相同,則表示:在集合新增中,認為是同一個"東西",覆蓋舊值。【==、equals、hashcode的區別和聯絡】
public V get(Object key) {
if (key == null)//key為null時特別處理
return getForNullKey();
Entry<K,V> entry = getEntry(key);
return null == entry ? null : entry.getValue();
}
final Entry<K,V> getEntry(Object key) {
if (size == 0) {
return null;
}
int hash = (key == null) ? 0 : hash(key);
//indexFor(hash, table.length) 根據hash值和陣列長度計算出下標,然後遍歷Entry連結串列
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
}
return null;
}6、確定陣列index:hashcode % table.length取模
按位取並,作用上相當於取模mod或者取餘%。這意味著陣列下標相同,並不表示hashCode相同。
static int indexFor(int h, int length) {
return h & (length-1);
}7、解決hash衝突的辦法
開放定址法(線性探測再雜湊,二次探測再雜湊,偽隨機探測再雜湊)
再雜湊法
鏈地址法
建立一個公共溢位區
Java中hashmap的解決辦法就是採用的鏈地址法。
8、再雜湊rehash過程
當雜湊表的容量超過預設容量時,必須調整table的大小。當容量已經達到最大可能值時,那麼該方法就將容量調整到Integer.MAX_VALUE返回,這時,需要建立一張新表,將原表的對映到新表中。
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
for (Entry<K,V> e : table) {
while(null != e) {
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}八、Hash應用例子
搜尋引擎會通過日誌檔案把使用者每次檢索使用的所有檢索串都記錄下來,每個查詢串的長度為1-255位元組。假設目前有一千萬個記錄(這些查詢串的重複度比較高,雖然總數是1千萬,但如果除去重複後,不超過3百萬個。一個查詢串的重複度越高,說明查詢它的使用者越多,也就是越熱門。),請你統計最熱門的10個查詢串,要求使用的記憶體不能超過1G。
第一步:Query統計
1、直接排序法
首先我們最先想到的的演算法就是排序了,首先對這個日誌裡面的所有Query都進行排序,然後再遍歷排好序的Query,統計每個Query出現的次數了。
但是題目中有明確要求,那就是記憶體不能超過1G,一千萬條記錄,每條記錄是255Byte,很顯然要佔據2.375G記憶體,這個條件就不滿足要求了。
讓我們回憶一下資料結構課程上的內容,當資料量比較大而且記憶體無法裝下的時候,我們可以採用外排序的方法來進行排序,這裡我們可以採用歸併排序,因為歸併排序有一個比較好的時間複雜度O(nlogn)。
排完序之後我們再對已經有序的Query檔案進行遍歷,統計每個Query出現的次數,再次寫入檔案中。
綜合分析一下,排序的時間複雜度是O(nlogn),而遍歷的時間複雜度是O(n),因此該演算法的總體時間複雜度就是O(n+nlogn)=O(nlogn)。
2、Hash Table法
在第1個方法中,我們採用了排序的辦法來統計每個Query出現的次數,時間複雜度是O(nlogn),那麼能不能有更好的方法來儲存,而時間複雜度更低呢?
題目中說明了,雖然有一千萬個Query,但是由於重複度比較高,因此事實上只有300萬的Query,每個Query 255Byte,因此我們可以考慮把他們都放進記憶體中去,而現在只是需要一個合適的資料結構,在這裡,Hash Table絕對是我們優先的選擇,因為Hash Table的查詢速度非常的快,幾乎是O(1)的時間複雜度。
那麼,我們的演算法就有了:維護一個Key為Query字串,Value為該Query出現次數的HashTable,每次讀取一個Query,如果該字串不在Table中,那麼加入該字串,並且將Value值設為1;如果該字串在Table中,那麼將該字串的計數加一即可。最終我們在O(n)的時間複雜度內完成了對該海量資料的處理。
本方法相比演算法1:在時間複雜度上提高了一個數量級,為O(n),但不僅僅是時間複雜度上的優化,該方法只需要IO資料檔案一次,而演算法1的IO次數較多的,因此該演算法2比演算法1在工程上有更好的可操作性。
第二步:找出Top 10
演算法一:普通排序
我想對於排序演算法大家都已經不陌生了,這裡不在贅述,我們要注意的是排序演算法的時間複雜度是O(nlogn),在本題目中,三百萬條記錄,用1G記憶體是可以存下的。
演算法二:部分排序
題目要求是求出Top 10,因此我們沒有必要對所有的Query都進行排序,我們只需要維護一個10個大小的陣列,初始化放入10個Query,按照每個Query的統計次數由大到小排序,然後遍歷這300萬條記錄,每讀一條記錄就和陣列最後一個Query對比,如果小於這個Query,那麼繼續遍歷,否則,將陣列中最後一條資料淘汰,加入當前的Query。最後當所有的資料都遍歷完畢之後,那麼這個陣列中的10個Query便是我們要找的Top10了。
不難分析出,這樣,演算法的最壞時間複雜度是N*K, 其中K是指top多少。
演算法三:堆
在演算法二中,我們已經將時間複雜度由NlogN優化到NK,不得不說這是一個比較大的改進了,可是有沒有更好的辦法呢?
分析一下,在演算法二中,每次比較完成之後,需要的操作複雜度都是K,因為要把元素插入到一個線性表之中,而且採用的是順序比較。這裡我們注意一下,該陣列是有序的,一次我們每次查詢的時候可以採用二分的方法查詢,這樣操作的複雜度就降到了logK,可是,隨之而來的問題就是資料移動,因為移動資料次數增多了。不過,這個演算法還是比演算法二有了改進。
基於以上的分析,我們想想,有沒有一種既能快速查詢,又能快速移動元素的資料結構呢?回答是肯定的,那就是堆。
藉助堆結構,我們可以在log量級的時間內查詢和調整/移動。因此到這裡,我們的演算法可以改進為這樣,維護一個K(該題目中是10)大小的小根堆,然後遍歷300萬的Query,分別和根元素進行對比。
思想與上述演算法二一致,只是演算法在演算法三,我們採用了最小堆這種資料結構代替陣列,把查詢目標元素的時間複雜度有O(K)降到了O(logK)。
那麼這樣,採用堆資料結構,演算法三,最終的時間複雜度就降到了N‘logK,和演算法二相比,又有了比較大的改進。
總結:
至此,演算法就完全結束了,經過上述第一步、先用Hash表統計每個Query出現的次數,O(N);然後第二步、採用堆資料結構找出Top 10,N*O(logK)。所以,我們最終的時間複雜度是:O(N)+N'*O(logK)。(N為1000萬,N’為300萬)。如果各位有什麼更好的演算法,歡迎留言評論。
九、參考:
http://www.cnblogs.com/wangjy/archive/2011/09/08/2171638.html
Java集合類之HashMap原始碼分析: http://www.open-open.com/lib/view/open1363245226500.html#
http://kb.cnblogs.com/page/189480/