學校實行學分制。每門的必修課都有固定的學分，同時還必須獲得相應的選修課程學分。學校開設了N（N<300）門的選修課程，每個學生可選課程的數量M是給定的。學生選修了這M門課並考核通過就能獲得相應的學分。
在選修課程中，有些課程可以直接選修，有些課程需要一定的基礎知識，必須在選了其它的一些課程的基礎上才能選修。例如《Frontpage》必須在選修了《Windows操作基礎》之後才能選修。我們稱《Windows操作基礎》是《Frontpage》的先修課。每門課的直接先修課最多隻有一門。兩門課也可能存在相同的先修課。每門課都有一個課號，依次為1，2，3，…。 例如:
表中1是2的先修課，2是3、4的先修課。如果要選3，那麼1和2都一定已被選修過。 　　你的任務是為自己確定一個選課方案，使得你能得到的學分最多，並且必須滿足先修課優先的原則。假定課程之間不存在時間上的衝突。
格式

輸入
輸入檔案的第一行包括兩個整數N、M（中間用一個空格隔開）其中1≤N≤300,1≤M≤N。
以下N行每行代表一門課。課號依次為1，2，…，N。每行有兩個數（用一個空格隔開），第一個數為這門課先修課的課號（若不存在先修課則該項為0），第二個數為這門課的學分。學分是不超過10的正整數。

輸出
輸出檔案每行只有一個數。第一行是實際所選課程的學分總數。
樣例1

樣例輸入1
7 4
2 2
0 1
0 4
2 1
7 1
7 6
2 2
樣例輸出1
13

這道題是不是比較噁心？
這和我們之前做的題不同，他這裡不是二叉樹，而是多叉樹。
而且….
可能A節點有5個兒子，而B節點只有1個兒子..
這麼噁心的東東，就要有噁心的演算法來對付他
在發程式碼之前，我們先說一個森林轉二叉樹的東東

森林裡面有什麼？樹啊
這麼多的樹我們要把它轉成一棵二叉樹？

不急，我們先將將一棵樹轉為一棵二叉樹

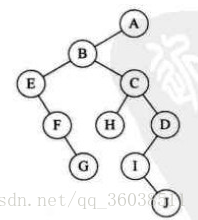
這是一棵樹：

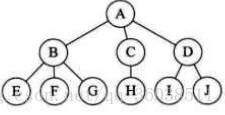
對你沒看錯這是一棵可（惡）愛（心）的樹樹

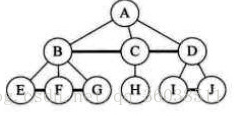
我們給同級的兄弟們加上了線
讓他們成為了一個整體

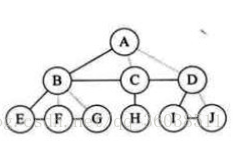
我們給除了跟第一個左孩子
和與你同級的第一個左孩子
連線
剩下的線全部去掉！！！
嗯這些線賊噁心我們去掉去掉

整理一波 二叉樹耶！

至於森林轉二叉樹

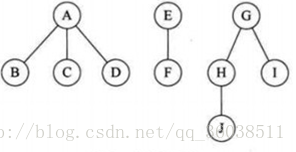
首先這是一片森林（是的我沒逗你）

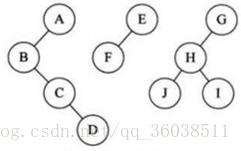
然後我們按剛剛的方法修建一下這些樹樹
變成幾棵二叉樹

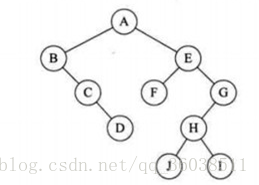
以第一棵樹為根節點
每一棵轉化而來的二叉樹都作為前一棵樹的右孩子
然後
神奇的事情發生了
二叉樹！！

然而剛才講這麼多
好像
好像對於這道題並沒有什麼卵用得
是的我們只需要用到第一步就夠了
程式碼：

#include <cstdio>
#include <cstring>
using namespace std;
struct node
{
    int lc,rc,c,v;
    //lc（左兒子）:他真正的兒子
    //rc（右兒子）:他的兄弟
    node()
    {
        lc=rc=-1;c=0;v=0;
    }
}a[11000];
int f[1100][1100];
int mymax(int x,int y) 
{
    return x>y?x:y;
}
int treedp(int x,int y)
{
    if (x<0||y<0) return 0;
    if (f[x][y]!=-1) return f[x][y];
    int maxx=0;
    for (int i=0;i<=y;i++)//列舉
    {
        int ls=y-i-1,rs=i;
        //分成左右兩部分，左邊ls分，右邊rs分
        int lss=0,rss=0;
        if (a[x].lc!=-1) lss=f[a[x].lc][ls]=treedp(a[x].lc,ls);
        if (a[x].rc!=-1) rss=f[a[x].rc][rs]=treedp(a[x].rc,rs);
        if (ls<0) maxx=mymax(maxx,rss);
        else maxx=mymax(maxx,lss+rss+a[x].c);
    }
    return maxx;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
    {
        int x;
        scanf("%d%d",&x,&a[i].c);
        //講這麼多其實寫出來就一個if語句
        if (a[x].v==0) a[x].lc=i;//如果他沒有兒子就把它收為他的左兒子
        else a[a[x].v].rc=i;//否則就把它作為他兒子的兄弟（就是他左兒子的右兒子）
        a[x].v=i;
    }
    memset(f,-1,sizeof(f));
    for (int i=1;i<=n;i++)
        f[i][0]=0;
    printf("%d\n",treedp(0,m+1));
    return 0;
}