1. 封裝成幀
2. 透明傳輸
3. 差錯控制

封裝成幀 ：
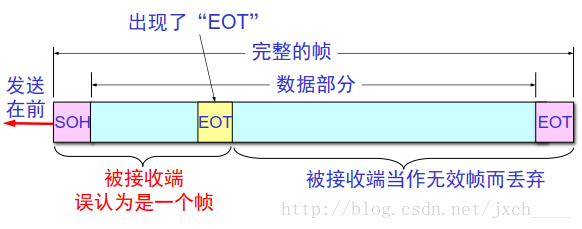
封裝成幀(framing)就是在一段資料的前後分別新增首部和尾部，然後就構成了一個幀。確定幀的界限。
用控制字元進行幀定界的方法舉例 ：

• SOH(Start Of Head):0x01
• EOT(End Of Transmission):0x04

透明傳輸 ：

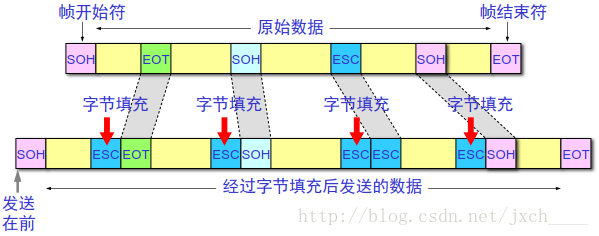
解決透明傳輸問題：位元組填充(byte stuffing)或字元填充(character stuffing)
傳送端的資料鏈路層在資料中出現的控制字元“SOH”或“EOT”前插入一轉義字元“ESC”。接收端的資料鏈路層在將資料送往網路層之前刪除插入的轉義字元。 ESC:0x1B

如果轉義字元也出現數據當中，怎麼辦？
在轉義字元前面再插入一個轉義字元。

差錯控制 ：
在傳輸過程中可能會產生位元差錯：1 可能會變成 0 而 0 也可能變成 1。 在一段時間內，傳輸錯誤的位元佔所傳輸位元總數的比率稱為誤位元速率 BER (Bit Error Rate)。 誤位元速率與信噪比有很大的關係。為了保證資料傳輸的可靠性，在計算機網路傳輸資料時，必須採用各種差錯檢測措施。 在資料鏈路層傳送的幀中，廣泛使用迴圈冗餘檢驗 CRC 檢錯技術。

迴圈冗餘檢驗的原理：
在傳送端，先把資料 M 劃分為組。假定每組 k 個位元，則需在 M 後面再新增供差錯檢測用的n 位冗餘碼

n 位冗餘碼的計算方法：
假設 M 分為一組，即 k = length(M) .

1. 選定長度為 (n + 1) 位的除數P
2. 用二進位制模 2 運算進行 2n 乘M 的運算，並以此結果為被除數。
3. 將得到的 (k + n) 位被除數除以除數P，得出商Q ，餘數R，餘數R即為所求n位冗餘碼。

例：M = 101001（k = 6）
設 n = 3, 除數 P = 1101， 被除數是 2nM = 101001000。 模 2 運算的結果是：商 Q = 110101， 餘數 R = 001。 把餘數 R 作為冗餘碼新增在資料 M 的後面傳送出去。傳送的資料是：2nM + R 即：101001001，共 (k + n) 位。

接收端對收到的每一幀進行 CRC 檢驗

• 若得出的餘數 R = 0，則判定這個幀沒有差錯，就接受(accept)。
• 若餘數 R = 0，則判定這個幀有差錯，就丟棄。

但這種檢測方法並不能確定究竟是哪一個或哪幾個比特出現了差錯。 只要經過嚴格的挑選，並使用位數足夠多的除數 P，那麼出現檢測不到的差錯的概率就很小很小。
僅用迴圈冗餘檢驗CRC差錯檢測技術只能做到無差錯接受(accept)。“無差錯接受”指：“凡是接受的幀（即不包括丟棄的幀），我們都能以非常接近於1的概率認為這些幀在傳輸過程中沒有產生差錯”。要做到“可靠傳輸”（即傳送什麼就收到什麼）就必須再加上確認和重傳機制。

幀檢驗序列 FCS
在資料後面新增上的冗餘碼稱為幀檢驗序列 FCS (Frame Check Sequence)。
CRC、FCS區別 ：

• CRC 是一種常用的檢錯方法，而 FCS 是新增在資料後面的冗餘碼。
• FCS 可以用 CRC 這種方法得出，但 CRC 並非用來獲得 FCS 的唯一方法。

例：
要傳送的資料為1101011011 。採用CRC的生成多項式是P(X) = X⁴ + X + 1 。

1. 試求應新增在資料後面的餘數。
2. 資料在傳輸過程中最後一個1變成了0，問接收端能否發現？
3. 資料在傳輸過程中最後兩個1變成了0，問接收端能否發現？
4. 採用CRC檢驗後，資料鏈路層的傳輸是否就變成了可靠的傳輸？

P(X) = X⁴ + X + 1 。// 第0、1、4位為1，其餘位為0 。
P = 10011， n = 4 。// p有5位，所以n = 5 - 1 = 4 。
2⁴ * 1101011011 = 11010110110000 。
11010110110000 / 10011 餘數為 1110 。
新增的檢驗序列是1110；2、3均可發現。
缺乏重傳機制，資料鏈路層的傳輸是不可靠的傳輸。