一、蒙特卡洛（Monte Carlo）方法簡介

蒙特卡洛是一個地名，位於賭城摩納哥，象徵概率。蒙特卡洛（Monte Carlo）方法是由大名鼎鼎的數學家馮·諾伊曼提出的，誕生於上世紀40年代美國的“曼哈頓計劃”。原理是通過大量隨機樣本，去了解一個系統，進而得到所要計算的值。

二、計算圓周率π的原理

一個正方形內部相切一個圓，圓和正方形的面積之比是π/4。

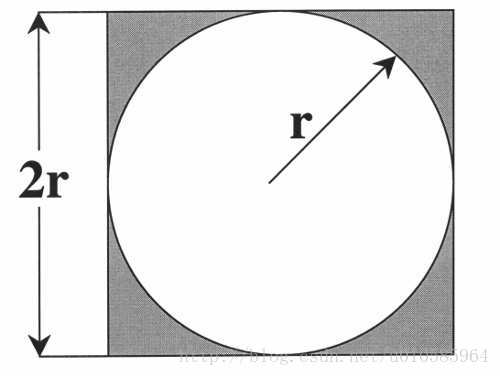
在這個正方形內部，隨機產生n個點（這些點服從均勻分佈），計算它們與中心點的距離是否大於圓的半徑，以此判斷是否落在圓的內部。統計圓內的點數，與n的比值乘以4，就是π的值。理論上，n越大，計算的π值越準。

三、matlab模擬試驗

matlab程式碼：
monte_carlo_method.m

%% Monte Carlo方法計算π
%正方形內部有一個相切的圓，它們的面積之比是π/4
clc,clear
r=1;
center_x=1;
center_y=1;
num=100000;%隨機樣本數
fprintf('開始Monte Carlo方法計算圓周率π,隨機樣本數為%d...\n',num);
s=rng;
rng(s);
sample_point=2*rand(2,num);
total_in=0;
for i=1:num
    distance=sqrt((sample_point(1,i)-1)^2+(sample_point(2,i)-1)^2);
    if distance<1
 

        total_in=total_in+1;
    end
end
my_pi=total_in/num*4;
fprintf('result:\nπ=%.4f\n',my_pi);
error=abs((pi-my_pi)/pi);
fprintf('誤差：%.4f\n',error);
fprintf('完成!\n');

%% 繪圖
fprintf('開始繪圖...');
figure
scatter(sample_point(1,:),sample_point(2,:),'bo');hold on
circle(1,[1,1]);
title('Monte Carlo方法計算圓周率π'
 
),xlabel('x'),ylabel('y')
axis([0,2,0,2])
fprintf('完成!\n');

circle.m

function circle(R,Center)
alpha=0:pi/50:2*pi;%角度[0,2*pi]
% R=2;%半徑
% Center=[1,1];%圓心
x=R*cos(alpha)+Center(1);
y=R*sin(alpha)+Center(2);
plot(x,y,'g-','LineWidth',2)
end

試驗結果：

1. 隨機樣本數為10000
   
   執行結果：
   π=3.1148
   誤差：0.0085

2. 隨機樣本數為100000
   
   執行結果：
   π=3.1468
   誤差：0.0017