1.float和double的範圍和精度

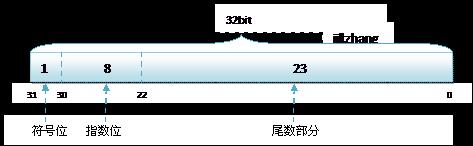
        float和double的範圍是由指數的位數來決定的。float的指數位有8位，而double的指數位有11位，分佈如下：
float：1bit（符號位）+8bits（指數位+23bits（尾數位）
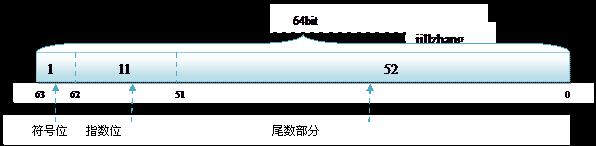
double：1bit（符號位）+ 11bits（指數位）+ 52bits（尾數位）
        在數學中，特別是在計算機相關的數字（浮點數）問題的表述中，有一個基本表達法：
　　　value of floating-point = significand x base ^ exponent , with sign --- F.1
　　譯為中文表達即為：
　　　（浮點）數值 =      尾數    ×    底數 ^ 指數，（附加正負號）---------------- F.2
於是，float的指數範圍為-127~128，而double的指數範圍為-1023~1024，並且指數位是按補碼的形式來劃分的。其中負指數決定了浮點數所能表達的絕對值最小的數；而正指數決定了浮點數所能表達的絕對值最大的數，也即決定了浮點數的取值範圍。float的範圍為-2^128 ~ +2^128，也即-3.40E+38 ~ +3.40E+38；double的範圍為-2^1024 ~ +2^1024，也即-1.79E+308 ~ +1.79E+308。

        float和double的精度是由尾數的位數來決定的。浮點數在記憶體中是按科學計數法來儲存的，其整數部分始終是一個隱含著的“1”，由於它是不變的，故不能對精度造成影響。
float：2^23 = 8388608，共七位，意味著最多能有7位有效數字，但絕對能保證的為6位，也即float的精度為6~7位有效數字；
double：2^52 = 4503599627370496，一共16位，同理，double的精度為15~16位。

2.C#/C++對於浮點數的儲存

        C 語言和C#語言中，對於浮點型別的資料採用單精度型別（float）和雙精度型別(double)來儲存，float資料佔用32bit, double資料佔用64bit,我們在宣告一個變數float f= 2.25f的時候，是如何分配記憶體的呢？如果胡亂分配，那世界豈不是亂套了麼，其實不論是float還是double在儲存方式上都是遵從IEEE的規範的，float遵從的是IEEE R32.24 ,而double 遵從的是R64.53。

         無論是單精度還是雙精度在儲存中都分為三個部分：
        1.符號位(Sign) : 0代表正，1代表為負
        2.指數位（Exponent）:用於儲存科學計數法中的指數資料，並且採用移位儲存

        3.尾數部分（Mantissa）：尾數部分

2.1 float / double的儲存方式

 

          R32.24和R64.53的儲存方式都是用科學計數法來儲存資料的，比如8.25用十進位制的科學計數法表示就為:8.25*10e0,而120.5可以表示為:1.205*10e2, 。而計算機根本不認識十進位制的資料，他只認識0，1，所以在計算機儲存中，首先要將上面的數更改為二進位制的科學計數 法表示，8.25用二進位制表示可表示為1000.01。120.5用二進位制表示為：1110110.1用 二進位制的科學計數法表示1000.01可以表示為1.0001*2e3,1110110.1可以表示為1.1101101*2e6,任何一個數都的科學計數法表示都為1.xxx*2en, 尾數部分就可以表示為xxxx,第一位都是1嘛，幹嘛還要表示呀？可以將小數點前面的1省略，所以23bit的尾數部分，可以表示的精度卻變成了 24bit，道理就是在這裡，那24bit能精確到小數點後幾位呢，我們知道9的二進位制表示為1001，所以4bit能精確十進位制中的1位小數點， 24bit就能使float能精確到小數點後6位，而對於指數部分，因為指數可正可負，8位的指數位能表示的指數範圍就應該為:-127-128了，所以 指數部分的儲存採用移位儲存，儲存的資料為元資料+127，下面就看看8.25和120.5在記憶體中真正的儲存方式。

2.2 例項解析

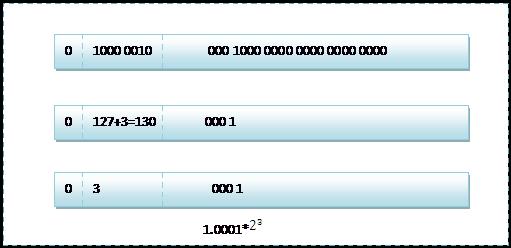
          首先看下8.25，用二進位制的科學計數法表示為:1.0001*2e3。按照上面的儲存方式，符號位為:0，表示為正，指數位為:3+127=130 ,尾數部分0001,故8.25的儲存方式如下圖所示:

          而單精度浮點數120.5的儲存方式如下圖所示: