Time Limit: 15 Sec Memory Limit: 357 MB
Submit: 808 Solved: 363
[Submit][Status][Discuss]
Description

很久很久以前，在遙遠的大陸上有一個美麗的國家。統治著這個美麗國家的國王是一個園藝愛好者，在他的皇家花園裡種植著各種奇花異草。有一天國王漫步在花園裡，若有所思，他問一個園丁道： “最近我在思索一個問題，如果我們把花壇擺成六個六角形，那麼……” “那麼本質上它是一個深度優先搜尋，陛下”，園丁深深地向國王鞠了一躬。 “嗯……我聽說有一種怪物叫九頭蛇，它非常貪吃蘋果樹……” “是的，顯然這是一道經典的動態規劃題，早在N元4002年我們就已經發現了其中的奧祕了，陛下”。 “該死的，你究竟是什麼來頭？” “陛下息怒，幹我們的這行經常莫名其妙地被問到和OI有關的題目，我也是為了預防萬一啊！” 王者的尊嚴受到了傷害，這是不可容忍的。看來一般的難題是難不倒這位園丁的，國王最後打算用車輪戰來消耗他的實力： “年輕人，在我的花園裡的每一棵樹可以用一個整數座標來表示，一會兒，我的騎士們會來輪番詢問你某一個矩陣內有多少樹，如果你不能立即答對，你就準備走人吧！”說完，國王氣呼呼地先走了。 這下輪到園丁傻眼了，他沒有準備過這樣的問題。所幸的是，作為“全國園丁保護聯盟”的會長——你，可以成
為他的最後一根救命稻草。

Input

第一行有兩個整數n，m（0≤n≤500000，1≤m≤500000）。n代表皇家花園的樹木的總數，m代表騎士們詢問的次數。 檔案接下來的n行，每行都有兩個整數xi，yi，代表第i棵樹的座標（0≤xi，yi≤10000000）。 檔案的最後m行，每行都有四個整數aj，bj，cj，dj，表示第j次詢問，其中所問的矩形以
（aj，bj）為左下座標，以（cj，dj）為右上座標。

Output

共輸出m行，每行一個整數，即回答國王以（aj，bj）和（cj，dj）為界的矩形裡有多少棵樹。

Sample Input

3 1
0 0
0 1
1 0
0 0 1 1

Sample Output

3

HINT

Source

Sol:
Tell you a sad story:我本來沒想做這道題，結果我那道題需要這個思想，順手切了
先離散化，按x座標排序，樹狀陣列統計的是該x座標內的y座標內的樹的數量
等我畫個圖Wait

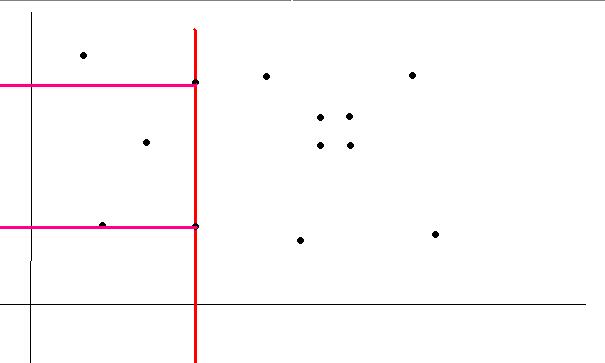
紅線表示當前的x軸，粉紅的線就是這個點統計的矩形內的點數，也就是樹狀陣列對應的y軸。
將點依次插入，講詢問拆成四個點，容斥一下下(或者叫差分?)即可。

#include<cstdio>
#include<algorithm>
using namespace std;
#define N 500005
#define X 10000005
inline int in(int x
 
=0,char ch=getchar()){while(ch>'9'||ch<'0') ch=getchar();
    while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x;}
struct Point{int x,y;}p[N];
struct Qus{int x,y,f,id;}q[N<<2];
inline bool operator < (const Point &a,const Point &b){return a.x<b.x;}
inline bool operator < (const Qus &a,const Qus &b){return a.x<b.x||(a.x==b.x&&a.y<b.y);}
int ans[N];int n,m,cnt;int d[X];
inline void Add(int x){for(;x<X;x+=x&-x) d[x]++;}
inline int Sum(int x,int res=0){for(;x;x-=x&-x) res+=d[x];return res;}
int main(){
    n=in(),m=in();int x1,y1,x2,y2;
    for(int i=1;i<=n;i++) p[i].x=in()+1,p[i].y=in()+1;
    for(int i=1;i<=m;i++){
        x1=in()+1,y1=in()+1,x2=in()+1,y2=in()+1;
        q[++cnt]=(Qus){x1-1,y1-1,1,i};
        q[++cnt]=(Qus){x1-1,y2,-1,i};
        q[++cnt]=(Qus){x2,y1-1,-1,i};
        q[++cnt]=(Qus){x2,y2,1,i};
    }
    sort(p+1,p+n+1);sort(q+1,q+cnt+1);
    for(int i=1,j=1;i<=cnt;i++){
        for(;j<=n&&p[j].x<=q[i].x;j++) Add(p[j].y);
        ans[q[i].id]+=Sum(q[i].y)*q[i].f;
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
    return 0;
}