神經網路的訓練過程，就是通過已有的樣本，求取使代價函式最小化時所對應的引數。代價函式測量的是模型對樣本的預測值與其真實值之間的誤差，最小化的求解一般使用梯度下降法（Gradient Decent）或其他與梯度有關的方法。其中的步驟包括：

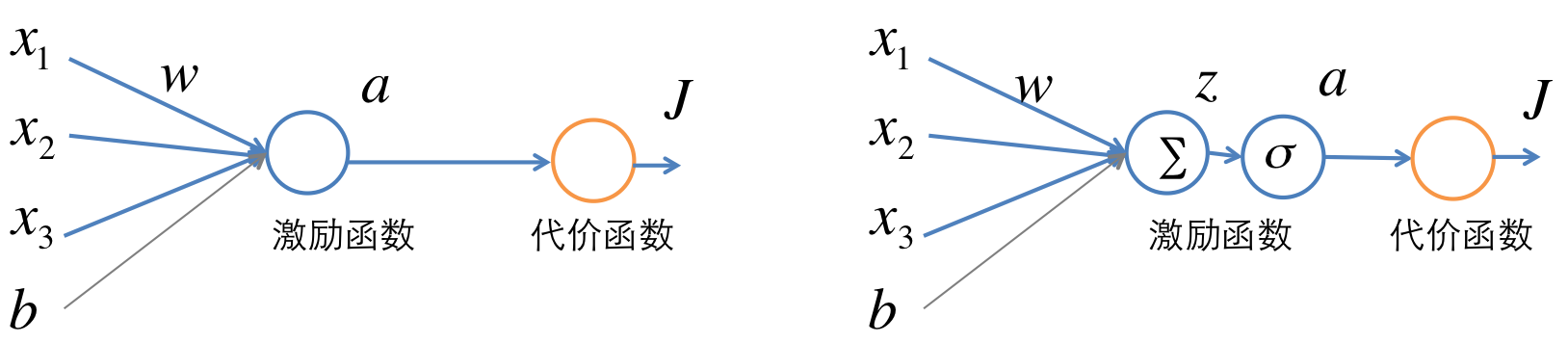
單個神經元的訓練

單個神經元的結構如下圖。假設一個訓練樣本為(x,y)。在下圖中，x是輸入向量，通過一個激勵函式hw,b(x)得到一個輸出a

，a再通過代價函式得到J。

f(W,b,x)=a=sigmoid(∑ixiwi+b) （公式1）
J(W,b,x,y)=12∥y−hw,b(x)∥2 （公式2）

這裡激勵函式以使用sigmoid為例，當然也可以使用其他的比如tanh或者rectived linear unit函式。要求的引數為W和b。

通過定義變數z=∑ixiwi+b可以將激勵函式看做是兩部分，如下圖右圖所示。第一部分是仿射求和得到z, 第二部分是通過sigmoid得到a。
這裡寫圖片描述

訓練過程中，要求代價函式J關於W和b的偏導數。先求J關於中間變數a和z的偏導：

δ(a)=∂∂aJ(W,b,x,y)=−(y−a

) （公式3）
δ(z)=∂∂zJ(W,b,x,y)=∂J∂a∂a∂z=δ(a)a(1−a) (公式4)

公式（4）中根據sigmoid函式的定義σ(z)=11+e−z可得∂a∂z=a(1−a)。

再根據鏈導法則，可以求得J關於W和b的偏導數，即得W和b的梯度。

∇WJ(W,b,x,y)=∂∂WJ=∂J∂z∂z∂W=δ(z)xT (公式5)

∇bJ(W,b,x,y)=∂∂bJ=∂J∂z∂z∂b=δ(z) (公式6)

在這個過程中，先求∂J/∂a,進一步求∂J/∂z,最後求得∂J/∂W和∂J/∂b。結合上圖及鏈導法則，可以看出這是一個將代價函式的增量∂J自後向前傳播的過程，因此稱為反向傳播（back propagation）。

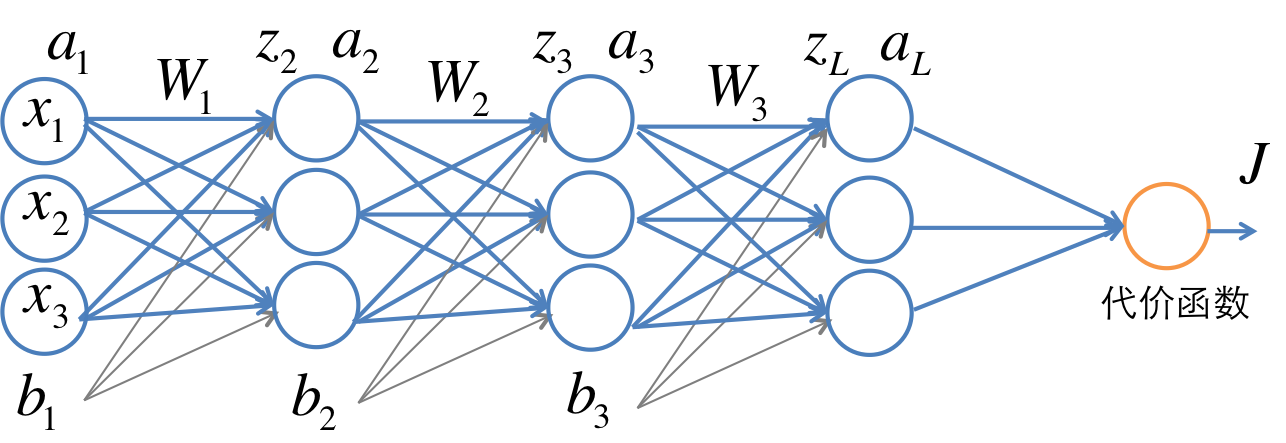
多層神經網路的訓練

多層網路的一個例子如下圖。
這裡寫圖片描述
假設第l+1層的輸入和輸出分別是