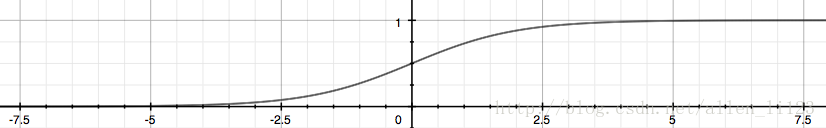吳恩達機器學習筆記(二)(附程式設計作業連結)
阿新 • • 發佈:2019-01-30
吳恩達機器學習筆記(二)
標籤: 機器學習
一.邏輯迴歸(logistic regression)
1.邏輯函式&&S型函式(logistic function and sigmoid function)
線性迴歸的假設表示式不試用於僅有0,1兩種結果的分類表達,將表示式簡單修改為邏輯函式也叫S型函式如下:
該函式的函式影象如下
在預測時輸入x變數所得的g(z)即結果為1的概率值
2.決策邊界(decision boundary)
在S型函式中若y大於0.5邊界則x必定大於0,於是:
所以可以推出以下結論!
3.代價函式(cost function)
分類問題的代價函式與迴歸問題的代價函式有一定的區別如下:
當y=1時函式影象如下
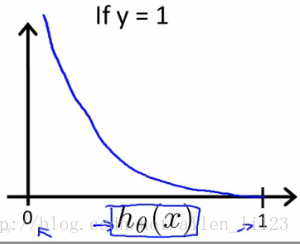
當y=0時函式影象如下
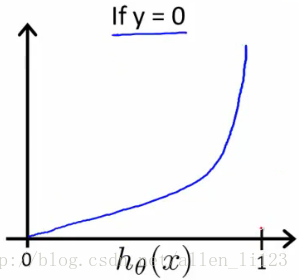
4.代價函式的簡化(Simplified Cost Function)
從而得到簡化的代價函式:
將其表達為矢量表達為:
5.梯度下降(Gradient Descent)
將其代價函式應用到梯度下降演算法中為: