前幾天有位同學問我一個問題，為什麼float和double不能直接用==比較？

例如：

1. System.out.println(0.1d == 0.1f);  

當時我只是簡單的回答，因為精度丟失，比較結果是不對的。

那麼，到底為什麼不對呢？ 此文略作整理記錄。

型別升級(type promotion)

首先，來看看Java中的幾種原生的數值型別進行==或!=比較運算的時候會發生什麼。

如果運算子兩邊的數值型別不同，則首先會進行型別升級(type promotion)，規則如下：

• 如果運算子任意一方的型別為double，則另一方會轉換為double
• 否則，如果運算子任意一方的型別為float，則另一方會轉換為float
• 否則，如果運算子任意一方的型別為long，則另一方會轉換為long
• 否則，兩邊都會轉換為int

然後，浮點數執行浮點數相等比較（int或者long執行整型相等比較）

那麼，上面那個例子，float首先會被升級為double，然後執行浮點數相等比較。那為什麼會返回flase呢？

1. System.out.println(0.1d == (double) 0.1f);  

舍入誤差(round-off error)

我們知道，根據IEEE 754，單精度的float是32位，雙精度的double為64位，如下圖：

其中，第一部分(s)為符號位，第二部分(exponent)為指數位，第三部分(mantissa)為基數部分。 這是科學計數法的二進位制表示。

那麼，既然位數是固定的，要表示像 1/3=0.3333333333333...或者pi=3.1415926..... 這樣的無限迴圈小數，就變得不可能了。

根據規範，則需要將不能標識的部分舍掉。

第二，還與10進位制不同的是，二進位制對於一些有限的小數，也不能精確的標示。比如像0.1這樣的小數，用二進位制也無法精確表示。所以，也需要舍掉。

補充：科學計數法及浮點數的二進位制表示

首先，再來回憶一下，科學計數法是什麼樣子的。一個數，可以有多重表示方法。

例如，254可以有但不僅僅有以下幾種表示：

上面這是10進位制的表示方式，也就是基數為10的表示方式。 基數，就是上面例子中 25.4 * 10 這裡的10，當然，指數是1.

但是如果基數是2，需要怎麼轉換呢？

看下面這個例子：

所以，經過這個轉換，就可以用IEEE 754表示一個浮點數了。

單精度轉換為雙精度會發生什麼

首先，我們來看，單精度浮點數0.1表示成二進位制會是什麼樣子的：

1. System.out.println(Integer.toBinaryString(Float.floatToIntBits(0.1f)));  

然後，雙精度的浮點數0.1的二進位制會是什麼樣子呢：

1. System.out.println(Long.toBinaryString(Double.doubleToLongBits(0.1d)));  

然後，在比較float==double的時候，首先，會將float進行型別升級，得到的新的double 的值會是什麼樣子：

1. System.out.println(Long.toBinaryString(Double.doubleToLongBits(0.1f)));  

1. System.out.println(Integer.toBinaryString(Float.floatToIntBits(0.1f)));  
2. System.out.println(Long.toBinaryString(Double.doubleToLongBits(0.1d)));  
3. System.out.println(Long.toBinaryString(Double.doubleToLongBits(0.1f)));  

用equals方法進行比較

既然，用==或者!=來比較非常坑爹，那可以用equals來進行比較嗎？ 我的答案是一定不能。

看看下面2個例子。

1. Double a = Double.valueOf("0.0");  
2. Double b = Double.valueOf("-0.0");  
3. System.out.println(a.equals(b));  

如果上面那個列子只是坑，下面這個簡直就是地雷了。

1. Double a = Math.sqrt(-1.0);  
2. Double b = 0.0d / 0.0d;  
3. Double c = a + 200.0d;  
4. Double d = b + 1.0d;  
5. System.out.println(a.equals(b));  
6. System.out.println(b.equals(c));  
7. System.out.println(c.equals(d));  

其實，在Java裡面，a和b表示為NaN(Not a Number)，既然不是數字，就無法比較嘛。

但是equals方法是比較2個物件是否等值，而不是物件的值是否相等，所以equals方法設計的初衷根本就不是用來做數值比較的。勿亂用。
關於equals方法，我另外一篇記錄會做更多解釋。

用compareTo方法進行比較

雖然說它在設計上是用於數值比較的，但它表現跟equals方法一模一樣——對於NaN和0.0與-0.0的比較上面。

另外，由於舍入誤差的存在，也可能會導致浮點數經過一些運算後，結果會有略微不同。

所以最好還是不要直接用Float.compareTo和Double.compareTo方法。

結論

在進行浮點數比較的時候，主要需要考慮3個因素

• NaN
• 無窮大/無窮小
• 舍入誤差

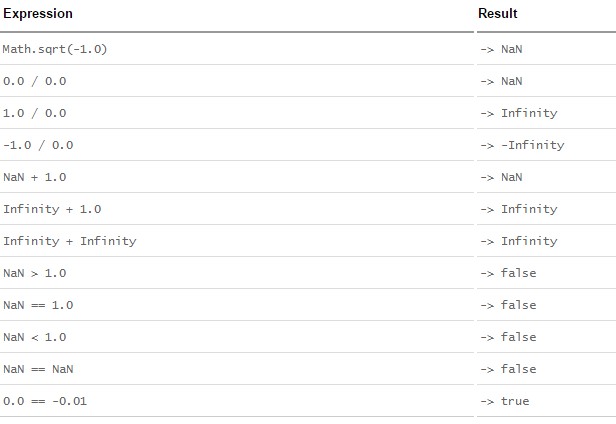
NaN和無窮出現的可能場景如下

所以，要比較浮點數是否相等，需要做的事情是：

• 排除NaN和無窮
• 在精度範圍內進行比較

例如下面的列子：

1. publicboolean isEqual(double a, double b) {  
2.     if (Double.isNaN(a) || Double.isNaN(b) || Double.isInfinite(a) || Double.isInfinite(b)) {  
3.         returnfalse;  
4.     }  
5.     return (a - b) < 0.001d;  
6. }  

它什麼都好，就是效率略低。需要自行在效能和精度之間取捨。

思考一下

為什麼下面這種方式可能會出現精度問題

1. BigDecimal.valueOf(0.1d);  
2. new BigDecimal(0.1d);  

引用列表