在.NET framework環境下，當我們的程式碼執行時，記憶體中有兩個地方用來儲存這些程式碼。假如你不曾瞭解，那就讓我來給你介紹棧(Stack)和堆(Heap)。棧和堆都用來幫助我們執行程式碼的，它們駐留在機器記憶體中，且包含所有程式碼執行所需要的資訊。

棧負責儲存我們的程式碼執行（或呼叫）路徑,而堆則負責儲存物件（或者說資料，接下來將談到很多關於堆的問題）的路徑。

可以將棧想象成一堆從頂向下堆疊的盒子。當每呼叫一次方法時，我們將應用程式中所要發生的事情記錄在棧頂的一個盒子中,而我們每次只能夠使用棧頂的那個盒子。當我們棧頂的盒子被使用完之後，或者說方法執行完畢之後，我們將拋開這個盒子然後繼續使用棧頂上的新盒子。堆的工作原理比較相似，但大多數時候堆用作儲存資訊而非儲存執行路徑，因此堆能夠在任意時間被訪問。與棧相比堆沒有任何訪問限制，堆就像床上的舊衣服，我們並沒有花時間去整理，那是因為可以隨時找到一件我們需要的衣服，而棧就像儲物櫃裡堆疊的鞋盒，我們只能從最頂層的盒子開始取，直到發現那隻合適的。

[heapvsstack1.gif]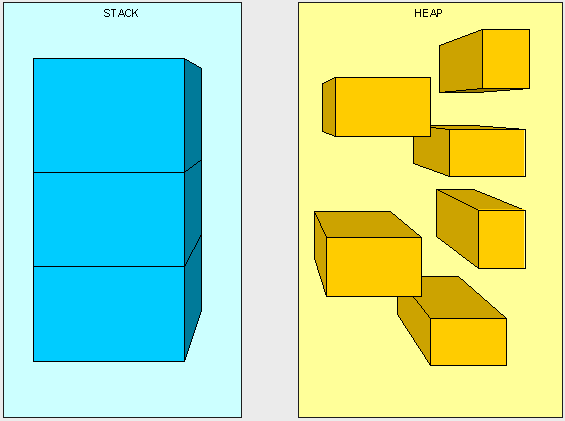

以上圖片並不是記憶體中真實的表現形式，但能夠幫助我們區分棧和堆。

棧是自行維護的，也就是說記憶體自動維護棧，當棧頂的盒子不再被使用，它將被丟擲。相反的，堆需要考慮垃圾回收，垃圾回收用於保持堆的整潔性，沒有人願意看到周圍都是贓衣服，那簡直太臭了！

堆疊是如何工作的:
棧是負責儲存我們的程式碼執行(或呼叫)時的路徑。當我們的程式碼開始呼叫一個方法時,將放置一段編碼指令(在方法中)到棧上,緊接著放置方法的引數，然後程式碼執行到方法中的被“壓棧”至棧頂的變數位置。通過以下例子很容易理解...

下面是一個方法（Method）:

           public int AddFive(int pValue)
          {
                int result;
                result = pValue + 5;
                return result;
          }

現在就來看看在棧頂發生了些什麼，記住我們所觀察的棧頂下實際已經壓入了許多別的內容。

首先方法（只包含需要執行的邏輯位元組，即執行該方法的指令，而非方法體內的資料）入棧，緊接著是方法的引數入棧。（我們將在後面討論更多的引數傳遞）

[heapvsstack3.gif]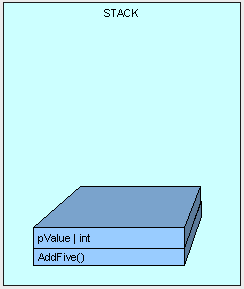

接著，控制（即執行方法的執行緒）被傳遞到堆疊中AddFive()的指令上，

[heapvsstack4.gif]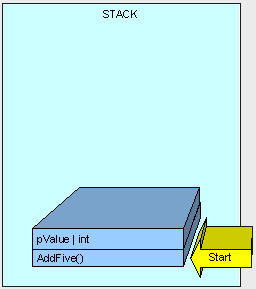

當方法執行時，我們需要在棧上為“result”變數分配一些記憶體，

[heapvsstack5.gif]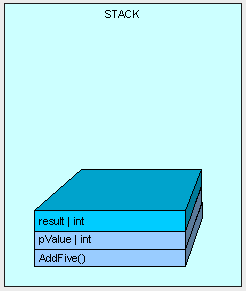

The method finishes execution and our result is returned.
方法執行完成，然後方法的結果被返回。

[heapvsstack6.gif]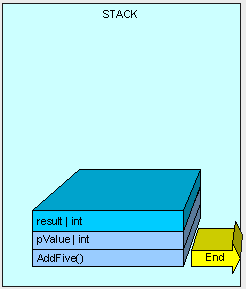

通過將棧指標指向AddFive()方法曾使用的可用的記憶體地址，所有在棧上的該方法所使用記憶體都被清空，且程式將自動回到棧上最初的方法呼叫的位置(在本例中不會看到)。

[heapvsstack7.gif]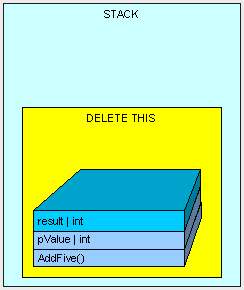

在這個例子中，我們的"result"變數是被放置在棧上的，事實上，當值型別資料在方法體中被宣告時，它們都是被放置在棧上的。

值型別資料有時也被放置在堆上。記住這條規則--值型別總是放在它們被宣告的地方。好的，如果一個值型別資料在方法體外被宣告，且存在於一個引用型別中，那麼它將被堆中的引用型別所取代。

來看另一個例子：

假如我們有這樣一個MyInt類（它是引用型別因為它是一個類型別）：

          public class MyInt
          {         
             public int MyValue;
          }

然後執行下面的方法:

          public MyInt AddFive(int pValue)
          {
                MyInt result = new MyInt();
                result.MyValue = pValue + 5;
                return result;
          }

就像前面提到的，方法及方法的引數被放置到棧上，接下來，控制被傳遞到堆疊中AddFive()的指令上。

[heapvsstack8.gif]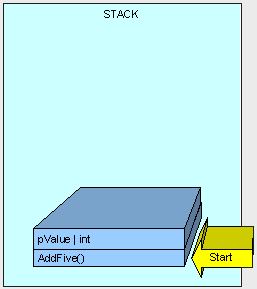

接著會出現一些有趣的現象...

因為"MyInt"是一個引用型別,它將被放置在堆上,同時在棧上生成一個指向這個堆的指標引用。

[heapvsstack9.gif]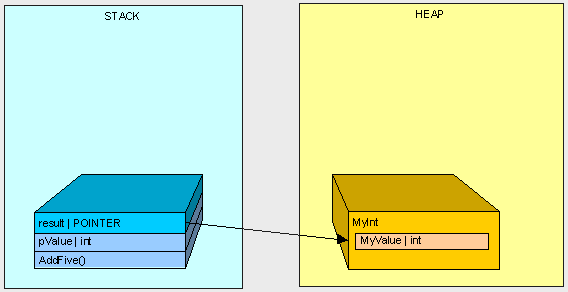

在AddFive()方法被執行之後，我們將清空...

[heapvsstack10.gif]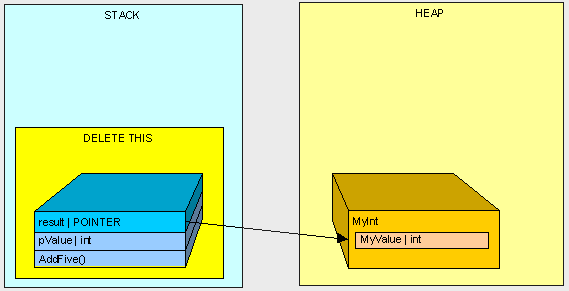

我們將剩下孤獨的MyInt物件在堆中（棧中將不會存在任何指向MyInt物件的指標!）

[heapvsstack11.gif]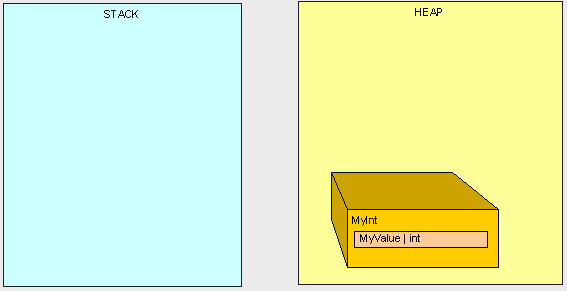

這就是垃圾回收器（後簡稱GC）起作用的地方。當我們的程式達到了一個特定的記憶體閥值，我們需要更多的堆空間的時候，GC開始起作用。GC將停止所有正在執行的執行緒，找出在堆中存在的所有不再被主程式訪問的物件，並刪除它們。然後GC會重新組織堆中所有剩下的物件來節省空間，並調整棧和堆中所有與這些物件相關的指標。你肯定會想到這個過程非常耗費效能，所以這時你就會知道為什麼我們需要如此重視棧和堆裡有些什麼，特別是在需要編寫高效能的程式碼時。

Ok... 這太棒了, 當它是如何影響我的？

Good question. 

當我們使用引用型別時，我們實際是在處理該型別的指標，而非該型別本身。當我們使用值型別時，我們是在使用值型別本身。聽起來很迷糊吧？

同樣，例子是最好的描述。

假如我們執行以下的方法：

          public int ReturnValue()
          {
                int x = new int();
                x = 3;
                int y = new int();
                y = x;     
                y = 4;         
                return x;
          }

我們將得到值3，很簡單，對吧？

假如我們首先使用MyInt類

     public class MyInt
          {
                public int MyValue;
          }

接著執行以下的方法：

          public int ReturnValue2()
          {
                MyInt x = new MyInt();
                x.MyValue = 3;
                MyInt y = new MyInt();
                y = x;                
                y.MyValue = 4;             
                return x.MyValue;
          }

我們將得到什麼？...    4!

為什麼？...  x.MyValue怎麼會變成4了呢？...  看看我們所做的然後就知道是怎麼回事了：

在第一例子中，一切都像計劃的那樣進行著：

          public int ReturnValue()
          {
                int x = 3;
                int y = x;   
                y = 4;
                return x;
          }

[heapvsstack12.gif]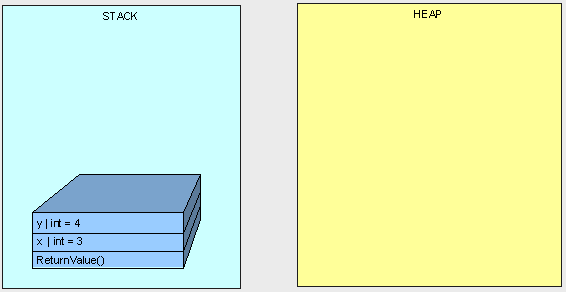

在第二個例子中，我們沒有得到"3"是因為變數"x"和"y"都同時指向了堆中相同的物件。
          public int ReturnValue2()
          {
                MyInt x;
                x.MyValue = 3;
                MyInt y;
                y = x;               
                y.MyValue = 4;
                return x.MyValue;
          }

[heapvsstack13.gif]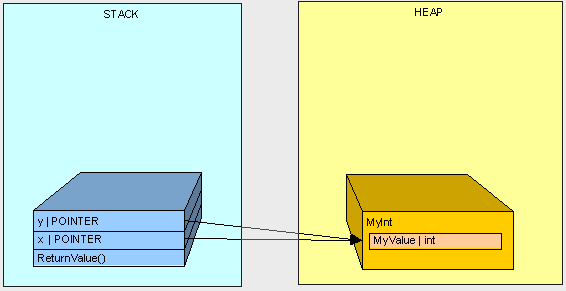

希望以上內容能夠使你對C#中的值型別和引用型別的基本區別有一個更好的認識，並且對指標及指標是何時被使用的有一定的基本瞭解。在系列的下一個部分，我們將深入記憶體管理並專門討論方法引數。