眾所周知，1+1=2，對於較小位數的加法，大家都可以在瞬間報出結果，但是如果比較大呢？13242345609745021+24234123421=?我們就需要一些運算時間來計算出結果。當然如果您是最強大腦選手，可能也能立刻報出答案。對於這種“最強大腦”選手，我們在FPGA中對應的就是效能，我們選擇成本更高的fpga比如您一開始使用的是cyclone I，現在換成了cyclone V系列產品，那麼運算速度就自然會提高。我們現在的想法就是想在同一個晶片上，減小運算的延時，從而提高系統的工作頻率，而不是通過改變器件。回想一下我們小學課上學的豎式加法運算我們想得到第k位的最終結果，就需要知道第k位的加數，被加數，以及是否進位，那麼進位又需要上一位的加數，被加數，進位數..以此類推直到第一位。這就是所謂的行波加法器了。

module add_4 ( 
input [3:0]a, 
input [3:0]b, 
input c_in, 
output [3:0] sum, 
output c_out 
); 
wire [3:0] c_tmp; 

full_adder i0 ( a[0], b[0], c_in, sum[0], c_tmp[0]); 
full_adder i1 ( a[1], b[1], c_tmp[0], sum[1], c_tmp[1] );  
full_adder i2 ( a[2], b[2], c_tmp[1], sum[2], c_tmp[2] );  
full_adder i3 ( a[3], b[3], c_tmp[2], sum[3], c_tmp[3] );  
assign c_out = c_tmp[3];
endmodule
 

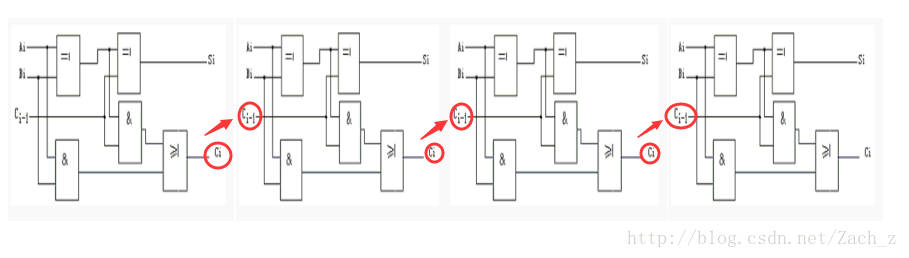這是我從網上找到的一張圖片，大概就是四個全加器級聯，怎麼個級聯方法呢，就是把他們的低位進位輸出連線到高位進位輸入。關於全加器，如果大家不會的話，還是先翻翻verilog書吧，建議還是先把基礎打好，因為這可以說是十分基本的內容了，任何一本verilog的書上肯定都會有的，我在這裡主要介紹的是他的加強版超前進位加法器。事實上，這個加法器需要9個門的傳輸延時，(第一個加法器需要三個，其他都是兩個)，於是我們想有沒有一種方法可以快一點，讓這個傳輸門的個數少一些呢，當然是可以的。這就是我要介紹的超前進位加法器了。大家可以先自己想想，對於一個四位加法器來說，我們如何可以立刻知道第k位的進位值呢？因為如果我們知道了該位的進位值，就僅需要一個全加器也就是3個門延時就能得到了結果了，這無疑是令人興奮的。
對於一個全加器我們知道Si =Ai ^ Bi^ Ci-1
Ci = AiBi + AiCi-1 + BiCi-1=AiBi + (Ai+Bi)Ci-1

令 Gi=Ai*Bi ; Pi=Ai+Bi 代入Ci =AiBi + (Ai+Bi)Ci-1
得 Ci=Gi+Gi*Ci-1

C0 = C_in
C1=G0 + P0·C0
C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0 ▪C0
C3=G2 + P2·C2 = G2 + P2·G1 + P2·P1·G0 + P2·P1·P0·C0
C4=G3 + P3·C3 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0 + P3·P2·P1·P0·C0
C_out=C4現在我們只需要三個門就可以實現四位加法運算了！

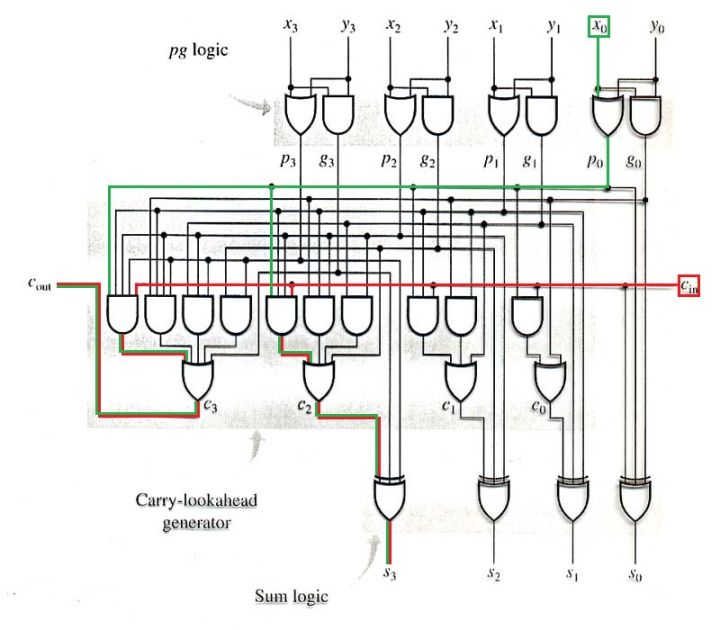
module ahead_adder4
(
input cin,
input [3:0]A,
input [3:0]B,
input [3:0]G,
input [3:0]P,
output  [3:0]S,
output   cout
);

wire [3:0]C;

assign C[0]= G[0] | (cin&P[0]);
assign C[1]= G[1] | (P[1]&G[0]) | (P[1]&P[0]&cin);
assign C[2]= G[2] | (P[2]&G[1]) | (P[2]&P[1]&G[0]) | (P[2]&P[1]&P[0]&cin);
assign C[3]= G[3] | (P[3]&G[2]) | (P[3]&P[2]&G[1]) | (P[3]&P[2]&P[1]&G[0]) | (P[3]&P[2]&P[1]&P[0]&cin);

assign S[0]=A[0]^B[0]^cin;
assign S[1]=A[1]^B[1]^C[0];
assign S[2]=A[2]^B[2]^C[1];
assign S[3]=A[3]^B[3]^C[2];
assign cout=C[3];

endmodule

那麼問題來了，如何實現16位超前進位加法器呢！？有一種辦法是將4個4位超前進位加法器級聯，但實際上這是一種超前+行波的方式，並不是最快的組合！事實上我們可以根據16位加數和被加數直接寫出這四個超前進位加法器的進位值，這樣即實現了超前進位的超前進位加法器！程式碼如下：

module ahead_adder
(
input [15:0]A,
input [15:0]B,
input CIN,
output reg [15:0]S,
output reg cout 
);

wire [15:0]G=A&B;
wire [15:0]P=A|B;
reg [3:0]cin;
wire cout1;

task ahead_adder4;

input cin;
input [3:0]A;
input [3:0]B;
input [3:0]G;
input [3:0]P;
output  reg [3:0]S;
output  reg cout;
reg [3:0]C;
begin
C[0]= G[0] | (cin&P[0]);
C[1]= G[1] | (P[1]&G[0]) | (P[1]&P[0]&cin);
C[2]= G[2] | (P[2]&G[1]) | (P[2]&P[1]&G[0]) | (P[2]&P[1]&P[0]&cin);
C[3]= G[3] | (P[3]&G[2]) | (P[3]&P[2]&G[1]) | (P[3]&P[2]&P[1]&G[0]) | (P[3]&P[2]&P[1]&P[0]&cin);

S[0]=A[0]^B[0]^cin;
S[1]=A[1]^B[1]^C[0];
S[2]=A[2]^B[2]^C[1];
S[3]=A[3]^B[3]^C[2];
cout=C[3];
end
endtask
task ahead_carry;

input cin;
input [15:0]G;
input [15:0]P;
output reg [3:0]cout;
reg [3:0]G2;
reg [3:0]P2;
begin

G2[0]=G[3] | P[3]&G[2] | P[3]&P[2]&G[1] | P[3]&P[2]&P[1]&G[0];
G2[1]=G[7] | P[7]&G[6] | P[7]&P[6]&G[5] | P[7]&P[6]&P[5]&G[4];
G2[2]=G[11] | P[11]&G[10] | P[11]&P[10]&G[9] | P[11]&P[10]&P[9]&G[8];
G2[3]=G[15] | P[15]&G[14] | P[15]&P[14]&G[13] | P[15]&P[14]&P[13]&G[12];

P2[0]=P[3]&P[2]&P[1]&P[0];
P2[1]=P[7]&P[6]&P[5]&P[4];
P2[2]=P[11]&P[10]&P[9]&P[8];
P2[3]=P[15]&P[14]&P[13]&P[12];

cout[0]=G2[0] | (cin&P2[0]);
cout[1]=G2[1] | (P2[1]&G2[0]) | (P2[1]&P2[0]&cin);
cout[2]=G2[2] | (P2[2]&G2[1]) | (P2[2]&P2[1]&G2[0]) | (P2[2]&P2[1]&P2[0]&cin);
cout[3]=G2[3] | (P2[3]&G2[2]) | (P2[3]&P2[2]&G2[1]) | (P2[3]&P2[2]&P2[1]&G2[0]) | (P2[3]&P2[2]&P2[1]&P2[0]&cin);
end
endtask

[email protected](*)
begin
	ahead_carry(CIN,G[15:0],P[15:0],cin[3:0]);
	ahead_adder4 (CIN,A[3:0],B[3:0],G[3:0],P[3:0],S[3:0],cout1);//因為進位值實際上已經被算出來了，所以這個cout1就沒有實際意義
	ahead_adder4 (cin[0],A[7:4],B[7:4],G[7:4],P[7:4],S[7:4],cout1);
	ahead_adder4 (cin[1],A[11:8],B[11:8],G[11:8],P[11:8],S[11:8],cout1);
	ahead_adder4 (cin[2],A[15:12],B[15:12],G[15:12],P[15:12],S[15:12],cout);//但是這個cout有實際意義，因為超前進位算出的是四個adder的低位進位值，沒有算最後一個的高位進位，所以要保留
end
endmodule