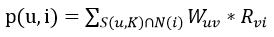上一篇講解了推薦演算法的分類，這裡電影推薦系統具體分析一下

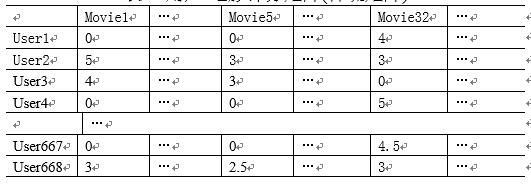
第一步：建立使用者電影矩陣模型

        如表1所示，協同過濾演算法的輸入資料通常表示為一個m*n的使用者評價矩陣Matrix，m是使用者數，n是電影數，Matrix[ij]表示第i個使用者對第j個電影的評價：

第二步：發現興趣相似的使用者

        這一階段，主要完成對目標使用者最近鄰居的查詢，通過計算目標使用者與其他使用者之間的相似度，得到與目標使用者最近的鄰居集。度量使用者間相似性：設N(u)為使用者u喜歡的電影集合，N(v)為使用者v喜歡的電影集合，將上一步中每行記錄視為一個向量，那麼u和v的相似度可通過以下進行計算：
        (a)採用Jaccard公式：W_uv=(|N(u)∩N(v)|)/(|N(u)∪N(v)|)
        (b)餘弦相似度計算：W_uv=(|N(u)∩N(v)|)/(√|N(u)||N(v)|)
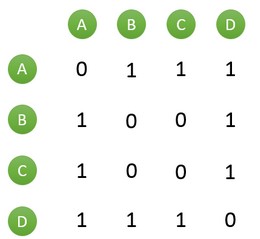
        這裡選擇餘弦公式進行相似度度量計算，假設目前共有4個使用者(A、B、C、D)，5部電影(a、b、c、d、e)，使用者與電影的關係如下圖所示：

        而這種方法的時間複雜度是O(|U|*|U|)，所以非常耗時。而在上表中可以看到“使用者-電影”表是一個稀疏矩陣，即很多時候N(u)^N(v)=0，如果換一下思路，可以首先計算N(u)^N(v)!=0的使用者，然後再計算sqrt(N(u)*N(v))。為此可以首先建立“電影-使用者”的倒排表，對每部電影都儲存電影到使用者的列表：

        設稀疏矩陣C[u][v]=N(u)^N(v)，在倒排索引中假設使用者u和使用者v同時屬於倒排索引中K部電影對應的使用者列表，就有C[u][v]=K。例如上圖所示只有電影a中同時出來了使用者有A和使用者B，則在矩陣中賦值為1：

        到此，使用者間的相似度計算就得到了，可以很直觀的找到與目標使用者興趣相似的使用者。

第三步：產生推薦專案

        需要從矩陣中找到與目標使用者最相似的K個使用者，用集合S(u,K)表示，將S中使用者喜歡的電影全部提取出來，併除去u已經喜歡的電影。對每個候選電影i，使用者對它的感興趣的程度用以下公式計算：

（其中Rvi表示使用者v對電影i的喜歡程度，此處舉例全部為1，在電影評分時應該代入使用者的評分）。
繼續上面的例子，假設我們給A推薦電影，選取K=3，對使用者A，電影c、e沒有看過，因此可以將這兩部電影推薦給使用者A，根據UserCF演算法使用者A對物品c、e的興趣分別計算p(A,c)和p(A,e)：