圖的表示方法

最常用的表示圖的方法是鄰接矩陣與鄰接表。

鄰接矩陣表示法

設G是一個有n(n>0)個頂點的圖，V(G)={v1, v2, …, vn}，則鄰接矩陣AG是一個n階二維矩陣。在該矩陣中，如果vi至vj有一條邊，則(i, j)項的值為1，否則為0，即：

鄰接矩陣的實現很簡單：

int edge[n][n]={0};

for(...){
    ...
    //無向圖的鄰接矩陣表示
    edge[node1][node2]=1;
    edge[node2][node1]=1;
}

鄰接表表示法

設G是一個有n(n>0)個頂點的圖，V(G)={v1, v2, …, vn}。在鄰接表中，每個頂點v都對應著一個連結串列，該連結串列的每個節點都包含一個頂點u，且(v, u)∈E(G)。因為圖中有n個頂點，所以可以利用一個長度為n的陣列A，A(i)指向第i個頂點對應的連結串列的第一個節點，連結串列由頂點vi的全部鄰接頂點組成。

實現鄰接表時，可以不用連結串列，而是用vector陣列的形式。

vector<int> adj[MAX];
for(int i=1;i<=n-1;i++) {
    cin>>a>>b;
    //構建無向圖的鄰接表
    adj[a].push_back(b);
    adj[b].push_back(a);
        }

其中，adj[i]是一個vector，它記錄了結點i連通的所有結點。

Dijkstra演算法

1.定義概覽

Dijkstra（迪傑斯特拉）演算法是典型的單源最短路徑演算法，用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件，直到擴充套件到終點為止。注意該演算法要求圖中不存在負權邊

問題描述：在無向圖 G=(V,E) 中，假設每條邊 E[i] 的長度為 w[i]，找到由頂點 V0 到其餘各點的最短路徑。（單源最短路徑）

2.演算法描述

求下圖中的1號頂點到2、3、4、5、6號頂點的最短路徑。

這裡使用二維陣列e來儲存頂點之間邊的關係，初始值如下：

我們還需要用一個一維陣列dis來儲存1號頂點到其餘各個頂點的初始路程，如下。

我們將此時dis陣列中的值稱為最短路的“估計值”。

既然是求1號頂點到其餘各個頂點的最短路程，那就先找一個離1號頂點最近的頂點。通過陣列dis可知當前離1號頂點最近是2號頂點。當選擇了2號頂點後，dis[2]的值就已經從“估計值”變為了“確定值”，即1號頂點到2號頂點的最短路程就是當前dis[2]值。

既然選了2號頂點，接下來再來看2號頂點有哪些出邊呢。有2->3和2->4這兩條邊。先討論通過2->3這條邊能否讓1號頂點到3號頂點的路程變短。也就是說現在來比較dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1號頂點到3號頂點的路程。dis[2]+e[2][3]中dis[2]表示1號頂點到2號頂點的路程，e[2][3]表示2->3這條邊。所以dis[2]+e[2][3]就表示從1號頂點先到2號頂點，再通過2->3這條邊，到達3號頂點的路程。

我們發現dis[3]=12，dis[2]+e[2][3]=1+9=10，dis[3]>dis[2]+e[2][3]，因此dis[3]要更新為10。這個過程有個專業術語叫做“鬆弛”。即1號頂點到3號頂點的路程即dis[3]，通過2->3這條邊鬆弛成功。

這便是Dijkstra演算法的主要思想：通過“邊”來鬆弛1號頂點到其餘各個頂點的路程。

同理通過2->4（e[2][4]），可以將dis[4]的值從∞鬆弛為4（dis[4]初始為∞，dis[2]+e[2][4]=1+3=4，dis[4]>dis[2]+e[2][4]，因此dis[4]要更新為4）。

剛才我們對2號頂點所有的出邊進行了鬆弛。鬆弛完畢之後dis陣列為：

接下來，繼續在剩下的3、4、5和6號頂點中，選出離1號頂點最近的頂點。通過上面更新過dis陣列，當前離1號頂點最近是4號頂點。此時，dis[4]的值已經從“估計值”變為了“確定值”。下面繼續對4號頂點的所有出邊（4->3，4->5和4->6）用剛才的方法進行鬆弛。鬆弛完畢之後dis陣列為：

繼續在剩下的3、5和6號頂點中，選出離1號頂點最近的頂點，這次選擇3號頂點。此時，dis[3]的值已經從“估計值”變為了“確定值”。對3號頂點的所有出邊（3->5）進行鬆弛。鬆弛完畢之後dis陣列為：

繼續在剩下的5和6號頂點中，選出離1號頂點最近的頂點，這次選擇5號頂點。此時，dis[5]的值已經從“估計值”變為了“確定值”。對5號頂點的所有出邊（5->4）進行鬆弛。鬆弛完畢之後dis陣列為：

最後對6號頂點所有點出邊進行鬆弛。因為這個例子中6號頂點沒有出邊，因此不用處理。到此，dis陣列中所有的值都已經從“估計值”變為了“確定值”。
最終dis陣列如下，這便是1號頂點到其餘各個頂點的最短路徑。

總結一下剛才的演算法。演算法的基本思想是：每次找到離源點（上面例子的源點就是1號頂點）最近的一個頂點，然後以該頂點為中心進行擴充套件，最終得到源點到其餘所有點的最短路徑。基本步驟如下：

1. 將所有的頂點分為兩部分：已知最短路程的頂點集合P和未知最短路徑的頂點集合Q。最開始，已知最短路徑的頂點集合P中只有源點s一個頂點。我們這裡用一個book[ i ]陣列來記錄哪些點在集合P中。例如對於某個頂點i，如果book[ i ]為1則表示這個頂點在集合P中，如果book[ i ]為0則表示這個頂點在集合Q中。
2. 設定源點s到自己的最短路徑為0即dis=0。若存在源點有能直接到達的頂點i，則把dis[ i ]設為e[s][ i ]。同時把所有其它（即源點不能直接到達的）頂點的最短路徑為設為∞。
3. 在Q中選擇一個離源點s最近的頂點u（即dis[u]最小）加入到P中。並考察所有以點u為起點的邊，對每一條邊進行鬆弛操作。
4. 重複第3步，如果集合Q為空，演算法結束。最終dis陣列中的值就是源點到所有頂點的最短路徑。

演算法的實現程式碼如下：

int main() {
    int n,m,s,t;//分別是節點數、邊的條數、起點、終點
    while(cin>>n>>m>>s>>t) {
        vector<vector<int>> edge(n+1,vector<int>(n+1,0));//鄰接矩陣
        vector<int> dis(n+1,0);//從起點出發的最短路徑
        vector<int> book(n+1,0);//某結點已經被訪問過

        for(int i=1;i<=n;i++)//初始化鄰接矩陣
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i<m;i++) {//讀入每條邊，完善鄰接矩陣
            cin>>u>>v>>length;
            if(length<edge[u][v]) {//如果當前的邊長比已有的短，則更新鄰接矩陣
                edge[u][v]=length;
                edge[v][u]=length;
            }
        }
        for(int i=1;i<=n;i++)//初始化dis陣列
            dis[i]=edge[s][i];
        book[s]=1;//把起點先標記一下

        //演算法核心！！！先確定沒訪問過的節點中，離起點最近的，然後鬆弛
        for(int i=1;i<=n;i++) {
            int min=INT_MAX;
            int index=0;
            for(int j=1;j<=n;j++) {
                if(book[j]==0 && dis[j]<min) {
                    min=dis[j];
                    index=j;
                }
            }
            book[index]=1;//標記這個剛剛被確定了的節點
            if(index==t) break;//如果已經到終點了，就直接結束

            for(int i=1;i<=n;i++) {//從剛被確定的節點出發，鬆弛剩下的節點
                if(book[i]==0 && edge[index][i]<INT_MAX && dis[i] > dis[index]+edge[index][i]) 
                    dis[i] = dis[index]+edge[index][i];
            }

        }
        cout<<dis[t]<<endl;
    }
    return 0;
}

通過上面的程式碼我們可以看出，這個演算法的時間複雜度是O(N2)。其中每次找到離1號頂點最近的頂點的時間複雜度是O(N)。

3. 如何記錄最短路徑

如果我們需要將那條最短路徑記錄下來，就要用到一個新陣列pre[]，在更新最短路徑時，將當前節點的前一個節點記錄下來，這樣，當最終確定最短路徑後，從後往前依次檢視pre陣列，就可以得到到達當前節點的最短路徑了。

Bellman-Ford演算法

1. 定義概覽

Bellman-Ford演算法是從DJ演算法引申出來的，它可以解決帶有負權邊的最短路徑問題。值得注意的是，DJ演算法和下面的Floyd演算法是基於鄰接矩陣的，而Bellman-Ford演算法是基於鄰接表，從邊的角度考量的。

2. 演算法描述

Bellman-Ford演算法用一句話概括就是：對所有的邊進行n-1次鬆弛操作。如果圖中存在最短路徑（即不存在負權迴路），那麼最短路徑所包含的邊最多為n-1條，也就是不可能包含迴路。因為如果存在正迴路，該路徑就不是最短的，而如果存在負迴路，就壓根就不存在所謂的最短路徑。

這裡，和用鄰接矩陣表示圖的方式不同，採用了u、v、w三個矩陣儲存邊的資訊。例如第i條邊（有向邊）儲存在u[i]、v[i]、w[i]中，表示從頂點u[i]到v[i]這條邊（u[i]->v[i]）的權值為w[i]。
之所以把dis[i]初始化為inf，可以理解成，初始時：從1號頂點通過0條邊到達其他頂點的路徑為正無窮。

int main() {
    int n,m,s,t;//分別是節點數、邊的條數、起點、終點
    while(cin>>n>>m>>s>>t) {
        vector<int> u(2*m+1,0);//某條邊的起點
        vector<int> v(2*m+1,0);//某條邊的終點
        vector<int> length(2*m+1,0);//某條邊的長度
        vector<int> dis(n+1,0);//從起點出發的最短路徑
        int num=0;
        for(int i=1;i<=m;i++) {//讀入每條邊
            num++;
            cin>>u[num]>>v[num]>>length[num];
            swap(u[num],v[num]);
        }
        for(int i=num+1;i<=2*num;i++) { //因為是無向圖，所以每條邊再複製一次，端點交換
            u[i]=v[i-num];
            v[i]=u[i-num];
            length[i]=length[i-num];
        }
        num=2*num;

        for(int i=1;i<=n;i++)//初始化dis陣列
            dis[i]=INT_MAX;
        dis[s]=0;

        for(int k=1;k<n;k++)
            for(int j=1;j<=num;j++) {
                if(dis[u[j]]<INT_MAX && dis[v[j]] > dis[u[j]]+length[j])
                    dis[v[j]] = dis[u[j]]+length[j];
            }

        cout<<dis[t]<<endl;
    }
    return 0;
}

對所有m條邊進行（n-1）輪鬆弛，第1輪的效果是得到從1號頂點“只經過一條邊”到達其餘各頂點的最短路徑長度，第2輪則是得到從1號頂點“經過最多兩條邊”到達其餘各頂點的最短路徑長度，第k輪則是得到從1號頂點“經過最多k條邊”到達其餘各頂點的最短路徑長度。

SPFA演算法

求單源最短路的SPFA演算法的全稱是：Shortest Path Faster Algorithm。 很多時候，給定的圖存在負權邊，這時類似Dijkstra等演算法便沒有了用武之地，而Bellman-Ford演算法的複雜度又過高，SPFA演算法便派上用場了。有人稱spfa演算法是最短路的萬能演算法。

演算法思想

設立一個佇列q用來儲存待優化的結點，優化時每次取出隊首結點u，並且用u點當前的最短路徑估計值對離開u點所指向的結點v進行鬆弛操作，如果v點的最短路徑估計值有所調整，且v點不在當前的佇列中，就將v點放入隊尾。這樣不斷從佇列中取出結點來進行鬆弛操作，直至佇列空為止。
鬆弛操作的原理是著名的定理：“三角形兩邊之和大於第三邊”，在資訊學中我們叫它三角不等式。所謂對結點i,j進行鬆弛，就是判定是否dis[j]>dis[i]+w[i,j]，如果該式成立則將dis[j]減小到dis[i]+w[i,j]，否則不動。
下面舉一個例項來說明SFFA演算法是怎樣進行的：

和BFS的區別

SPFA在形式上和廣度優先搜尋非常類似，不同的是BFS中一個點出了佇列就不可能重新進入佇列，但是SPFA中一個點可能在出佇列之後再次被放入佇列，也就是一個點改進過其它的點之後，過了一段時間可能本身被改進(重新入隊)，於是再次用來改進其它的點，這樣反覆迭代下去。

程式碼實現

int main() {
    int n,m,s,t;//分別是節點數、邊的條數、起點、終點

    while(cin>>n>>m>>s>>t) {
        vector<vector<int>> edge(n+1,vector<int>(n+1,0));//鄰接矩陣
        vector<int> dis(n+1,INT_MAX);//從起點出發的最短路徑
        vector<int> book(n+1,0);//某結點在佇列中
        queue<int> q;

        for(int i=1;i<=n;i++)//初始化鄰接矩陣
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i<m;i++) {//讀入每條邊，完善鄰接矩陣
            cin>>u>>v>>length;
            if(length<edge[u][v]) {//如果當前的邊長比已有的短，則更新鄰接矩陣
                edge[u][v]=length;
                edge[v][u]=length;
            }
        }

        dis[s]=0;
        book[s]=1;//把起點先放入佇列
        q.push(s);

        int top;
        while(!q.empty()) {//如果佇列非空
            top=q.front();//取出隊首元素
            q.pop();
            book[top]=0;//釋放隊首結點，因為這節點可能下次用來鬆弛其它節點，重新入隊

            for(int i=1;i<=n;i++) {
                if(edge[top][i]!=INT_MAX && dis[i]>dis[top]+edge[top][i]) {
                    dis[i]= dis[top]+edge[top][i]; //更新最短路徑
                    if(book[i]==0) { //如果擴充套件結點i不在佇列中，入隊
                        book[i]=1;
                        q.push(i);
                    }
                }
            }

        }
        cout<<dis[t]<<endl;
    }
    return 0;
}

如何輸出最短路徑

在一個圖中，我們僅僅知道結點A到結點E的最短路徑長度，有時候意義不大。這個圖如果是地圖的模型的話，在算出最短路徑長度後，我們總要說明“怎麼走”才算真正解決了問題。如何在計算過程中記錄下來最短路徑是怎麼走的，並在最後將它輸出呢？
我們定義一個path[]陣列，path[i]表示源點s到i的最短路程中，結點i之前的結點的編號(父結點)，我們在藉助結點u對結點v鬆弛的同時，標記下path[v]=u，記錄的工作就完成了。
如何輸出呢？我們記錄的是每個點前面的點是什麼，輸出卻要從最前面到後面輸出，這很好辦，遞迴就可以了：

void printpath(int k){
    if (path[k]!=0) printpath(path[k]);
    cout << k << ' ';
}

Floyd演算法

1.定義概覽

Floyd演算法（弗洛伊德演算法）是解決任意兩點間的最短路徑的一種演算法，可以正確處理有向（無向）圖的最短路徑問題，同時也被用於計算有向圖的傳遞閉包。Floyd演算法的時間複雜度為O(N3)，空間複雜度為O(N2)。

2.演算法描述

1)演算法思想原理

Floyd演算法是一個經典的動態規劃演算法。用通俗的語言來描述的話，首先我們的目標是尋找從點i到點j的最短路徑。從動態規劃的角度看問題，我們需要為這個目標重新做一個詮釋。
從任意節點i到任意節點j的最短路徑不外乎2種可能，一是直接從i到j，二是從i經過若干個節點k到j。所以，我們假設Dis(i,j)為節點u到節點v的最短路徑的距離，對於每一個節點k，我們檢查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，證明從i到k再到j的路徑比i直接到j的路徑短，我們便設定Dis(i,j) = Dis(i,k) + Dis(k,j)，這樣一來，當我們遍歷完所有節點k，Dis(i,j)中記錄的便是i到j的最短路徑的距離。

2).演算法描述

用一個數組來儲存任意兩個點之間的距離，注意，這裡可以是有向的，也可以是無向的。

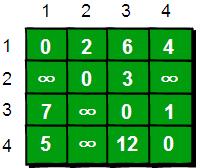
當任意兩點之間不允許經過第三個點時，這些城市之間最短路程就是初始路程。
如果現在只允許經過1號頂點，求任意兩點之間的最短路程，應該如何求呢？只需判斷e[i][1]+e[1][j]是否比e[i][j]要小即可。e[i][j]表示的是從i號頂點到j號頂點之間的路程。e[i][1]+e[1][j]表示的是從i號頂點先到1號頂點，再從1號頂點到j號頂點的路程之和。其中i是1~n迴圈，j也是1~n迴圈，程式碼實現如下。

for(i=1;i<=n;i++) {   
    for(j=1;j<=n;j++) {   
        if ( e[i][j] > e[i][1]+e[1][j] )   
            e[i][j] = e[i][1]+e[1][j];   
    }   
} 

在只允許經過1號頂點的情況下，任意兩點之間的最短路程更新為：

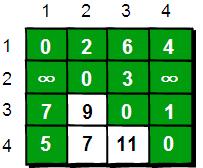
通過上圖我們發現：在只通過1號頂點中轉的情況下，3號頂點到2號頂點（e[3][2]）、4號頂點到2號頂點（e[4][2]）以及4號頂點到3號頂點（e[4][3]）的路程都變短了。

接下來繼續求在只允許經過1和2號兩個頂點的情況下任意兩點之間的最短路程。如何做呢？我們需要在只允許經過1號頂點時任意兩點的最短路程的結果下，再判斷如果經過2號頂點是否可以使得i號頂點到j號頂點之間的路程變得更短。即判斷e[i][2]+e[2][j]是否比e[i][j]要小，程式碼實現為如下：

//經過1號頂點   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
        if (e[i][j] > e[i][1]+e[1][j])  e[i][j]=e[i][1]+e[1][j];   
//經過2號頂點   
for(i=1;i<=n;i++)   
    for(j=1;j<=n;j++)   
        if (e[i][j] > e[i][2]+e[2][j])  e[i][j]=e[i][2]+e[2][j]; 

在只允許經過1和2號頂點的情況下，任意兩點之間的最短路程更新為：

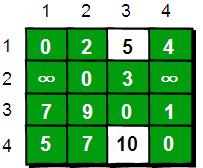
通過上圖得知，在相比只允許通過1號頂點進行中轉的情況下，這裡允許通過1和2號頂點進行中轉，使得e[1][3]和e[4][3]的路程變得更短了。

同理，繼續在只允許經過1、2和3號頂點進行中轉的情況下，求任意兩點之間的最短路程。任意兩點之間的最短路程更新為：

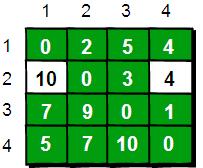
最後允許通過所有頂點作為中轉，任意兩點之間最終的最短路程為：

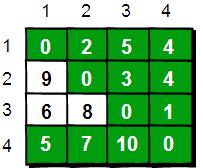
整個演算法過程雖然說起來很麻煩，但是程式碼實現卻非常簡單，核心程式碼只有五行：

for(k=1;k<=n;k++)   
    for(i=1;i<=n;i++)   
         for(j=1;j<=n;j++)   
             if(e[i][j]>e[i][k]+e[k][j])   
                 e[i][j]=e[i][k]+e[k][j]; 

這段程式碼的基本思想就是：最開始只允許經過1號頂點進行中轉，接下來只允許經過1和2號頂點進行中轉……允許經過1~n號所有頂點進行中轉，求任意兩點之間的最短路程。用一句話概括就是：從i號頂點到j號頂點只經過前k號點的最短路程。下面給出這個演算法的完整程式碼：

int main() {
    int n,m;
    while(cin>>n>>m) {
        vector<vector<int>> edge(n+1,vector<int>(n+1,0));

        for(int i=1;i<=n;i++)//初始化鄰接矩陣
            for(int j=1;j<=n;j++)
                if(i!=j) edge[i][j]=INT_MAX;

        int u,v,length;
        for(int i=0;i<m;i++) {
            cin>>u>>v>>length;
            if(length<edge[u][v]) {//如果當前的邊長比已有的短，則更新鄰接矩陣
                edge[u][v]=length;
                edge[v][u]=length;
            }
        }

        //核心程式碼！！！5行
        for(int k=1;k<=n;k++) 
            for(int i=1;i<=n;i++) 
                for(int j=1;j<=n;j++) 
                    if(edge[i][k]!=INT_MAX && edge[k][j]!=INT_MAX && edge[i][j] > edge[i][k]+edge[k][j])
                        edge[i][j] = edge[i][k]+edge[k][j];

        for(int i=1;i<=n;i++) {//輸出最終的鄰接矩陣
                for(int j=1;j<=n;j++) 
                    cout<<edge[i][j]<<' ';
                cout<<endl;
        }
    }
    return 0;
}

通過這種方法我們可以求出任意兩個點之間最短路徑。它的時間複雜度是O(N3)。令人很震撼的是它竟然只有五行程式碼，實現起來非常容易。正是因為它實現起來非常容易，如果時間複雜度要求不高，使用Floyd演算法來求指定兩點之間的最短路或者指定一個點到其餘各個頂點的最短路徑也是可行的。

另外需要注意的是：Floyd-Warshall演算法不能解決帶有“負權迴路”（或者叫“負權環”）的圖，因為帶有“負權迴路”的圖沒有最短路。例如下面這個圖就不存在1號頂點到3號頂點的最短路徑。因為1->2->3->1->2->3->…->1->2->3這樣路徑中，每繞一次1->-2>3這樣的環，最短路就會減少1，永遠找不到最短路。其實如果一個圖中帶有“負權迴路”那麼這個圖則沒有最短路。

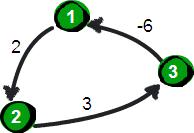
3種演算法的比較

適用情況

dj和ford演算法用於解決單源最短路徑，而floyd演算法解決多源最短路徑。

dj適用稠密圖（鄰接矩陣），因為稠密圖問題與頂點關係密切；
ford演算法適用稀疏圖（鄰接表），因為稀疏圖問題與邊關係密切。
floyd在稠密圖（鄰接矩陣）和稀疏圖（鄰接表）中都可以使用；

PS：dj演算法雖然一般用鄰接矩陣實現，但也可以用鄰接表實現，只不過比較繁瑣。而ford演算法只能用鄰接表實現。

dj演算法不能解決含有負權邊的圖；
而Floyd演算法和Ford演算法可以解決含有負權邊的問題，但都要求沒有總和小於0的負權環路。

SPFA演算法可以解決負權邊的問題，而且複雜度比Ford低。形式上，它可以看做是dj演算法和BFS演算法的結合。

3種演算法都是既能處理無向圖問題，也能處理有向圖問題。因為無向圖只是有向圖的特例，它們只是在鄰接矩陣或鄰接表的初始化時有所區別。

補充：A*演算法

A*演算法把Dijkstra演算法（靠近初始點的結點）和BFS演算法（靠近目標點的結點）的資訊塊結合起來。在討論A*的標準術語中，g(n)表示從初始結點到任意結點n的代價，h(n)表示從結點n到目標點的啟發式評估代價（heuristic estimated cost）。當從初始點向目標點移動時，A*權衡這兩者。每次進行主迴圈時，它檢查f(n)最小的結點n，其中f(n) = g(n) + h(n)。
具體的介紹可以見這篇部落格：
連結