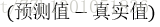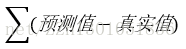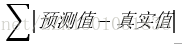2. 預測準確度
   2.1 評分預測
   評分預測的預測準確度可以通過均方根誤差（RMSE）和平均絕對誤差（MAE）計算。
   那麼RMSE和MAE的公式是怎麼推匯出來的呢？請看下面的解析：
   （1）我們對 某一使用者對某一物品的評分值 進行預測，要求預測值與實際值的偏差，從字面意思上便可以表示為（也就只有這一種方式），預測值與真實值兩者作差：
   
   （2）（1）中方法只適合於（某一使用者）對一個物品的評分值的預測，那如果該使用者對多個物品都會評分，要預測這樣的多個評分值呢？
   也可以從字面意思上表示，即將所有物品的預測值與實際值的偏差，加起來，即：
   
   （3）（2）中方法存在缺陷，仍需要進行改進。

其缺陷有兩個：
<1> 正負相消：每一個物品對應的（預測值-真實值），有正有負，在求和時，正偏差和負偏差會相互抵消掉。（在極端的情況下，若偏差有正負，並且最後全部抵消為0，那麼在整體上就會看起來，預測值與真實值沒有偏差，非常精準，這當然是不正確的。）
<2> 樣本總量影響偏差和
樣本總量越大，偏差的和越大。（偏差的正負可以忽略掉）

為了解決這兩個缺陷，可以分別採取措施應對：
<1>正負相消
可以採取的措施有：平方再開根號、取絕對值。
[1]平方再開根號

[2]取絕對值

<2> 樣本總量影響偏差和
可以採取的措施有：求平均數。
<1>中的兩個措施解決了正負相消的缺陷，現在再採用去絕對值得方式消除樣本總量的影響：
[1] 平方根再開根號 + 求平均數：

均方根誤差就是這麼來的：

只是這裡筆者有一個問題，按照筆者的思路，這一步的公式中只對分子開根號，不包括分母。然而RMSE的公式中，將分母也開根號了，這裡筆者沒有理解。所以還希望有明白的朋友在評論區分享一下自己的見解，互相學習，非常感謝。

[2] 取絕對值 + 求平均數：結果也就是平均絕對誤差

RMSE與MAE的優劣比較：
RMSE對異常值敏感，因為它的懲罰是平方的，所以異常值的損失非常大。[1]

參考文獻