一致性雜湊演算法與C++實現
一. 演算法解決問題
一致性雜湊演算法在1997年由麻省理工學院提出的一種分散式雜湊(DHT)實現演算法,設計目標是為了解決因特網中的熱點(Hot spot)問題,初衷和CARP十分類似。一致性雜湊修正了CARP使用的簡 單雜湊演算法帶來的問題,使得分散式雜湊(DHT)可以在P2P環境中真正得到應用。
一致性hash演算法提出了在動態變化的Cache環境中,判定雜湊演算法好壞的四個定義:
1、平衡性(Balance):平衡性是指雜湊的結果能夠儘可能分佈到所有的緩衝中去,這樣可以使得所有的緩衝空間都得到利用。很多雜湊演算法都能夠滿足這一條件。
2、單調性(Monotonicity):單調性是指如果已經有一些內容通過雜湊分派到了相應的緩衝中,又有新的緩衝加入到系統中。雜湊的結果應能夠保證原有已分配的內容可以被對映到原有的或者新的緩衝中去,而不會被對映到舊的緩衝集合中的其他緩衝區。
3、分散性
4、負載(Load):負載問題實際上是從另一個角度看待分散性問題。既然不同的終端可能將相同的內容對映到不同的緩衝區中,那麼對於一個特定的緩衝區而言,也可能被不同的使用者對映為不同 的內容。與分散性一樣,這種情況也是應當避免的,因此好的雜湊演算法應能夠儘量降低緩衝的負荷。
在分散式叢集中,對機器的新增刪除,或者機器故障後自動脫離叢集這些操作是分散式叢集管理最基本的功能。如果採用常用的hash(object)%N演算法,那麼在有機器新增或者刪除後,很多原有的資料就無法找到了,這樣嚴重的違反了單調性原則。接下來主要講解一下一致性雜湊演算法是如何設計的。
二. 設計方法
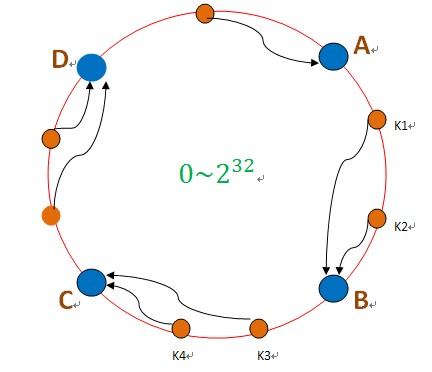
把資料用hash函式(如MD5,MurMurHash等演算法),對映到一個很大的空間裡,如圖所示。資料的儲存時,先得到一個hash值,對應到這個環中的每個位置,如k1對應到了圖中所示的位置,然後沿順時針找到一個機器節點B,將k1儲存到B這個節點中。
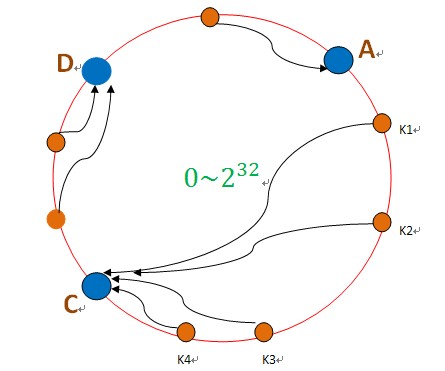
如果B節點宕機了,則B上的資料就會落到C節點上,如下圖所示:
這樣,只會影響C節點,對其他的節點A,D的資料不會造成影響。然而,這又會造成一個“雪崩”的情況,即C節點由於承擔了B節點的資料,所以C節點的負載會變高,C節點很容易也宕機,這樣依次下去,這樣造成整個叢集都掛了。
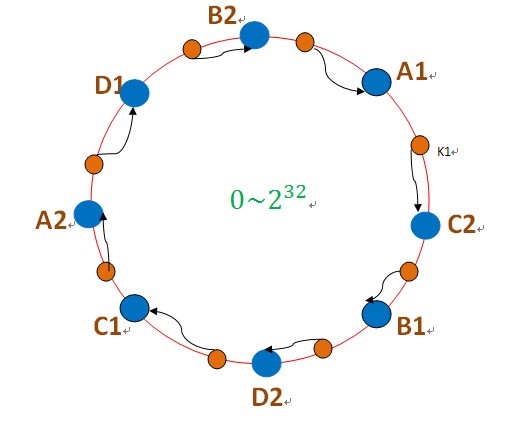
為此,引入了“虛擬節點”的概念:即把想象在這個環上有很多“虛擬節點”,資料的儲存是沿著環的順時針方向找一個虛擬節點,每個虛擬節點都會關聯到一個真實節點,如下圖所使用:
圖中的A1、A2、B1、B2、C1、C2、D1、D2都是虛擬節點,機器A負載儲存A1、A2的資料,機器B負載儲存B1、B2的資料,機器C負載儲存C1、C2的資料。由於這些虛擬節點數量很多,均勻分佈,因此不會造成“雪崩”現象。
三. 程式碼實現
MurMurHash演算法,是非加密HASH演算法,效能很高, 比傳統的CRC32, MD5,SHA-1(這兩個演算法都是加密HASH演算法,複雜度本身就很高,帶來的效能上的損害也不可避免) 等HASH演算法要快很多,而且這個演算法的碰撞率很低。所以這裡我們採用MurMurHash演算法
標頭檔案consistent_hash.h
#include <map>
using namespace std;
class ConsistentHash
{
public:
ConsistentHash(int node_num, int virtual_node_num);
~ConsistentHash();
void Initialize();
size_t GetServerIndex(const char* key);
void DeleteNode(const int index);
void AddNewNode(const int index);
private:
map<uint32_t,size_t> server_nodes_; //虛擬節點,key是雜湊值,value是機器的index
int node_num_;//真實機器節點個數
int virtual_node_num_;//每個機器節點關聯的虛擬節點個數
};實現檔案consistent_hash.cpp
#include <map>
#include <string.h>
#include <sstream>
#include "consistent_hash.h"
#include "murmurhash3.h"
using namespace std;
ConsistentHash::ConsistentHash(int node_num, int virtual_node_num)
{
node_num_ = node_num;
virtual_node_num_ = virtual_node_num;
}
ConsistentHash::~ConsistentHash()
{
server_nodes_.clear();
}
void ConsistentHash::Initialize()
{
for(int i=0; i<node_num_; ++i)
{
for(int j=0; j<virtual_node_num_; ++j)
{
stringstream node_key;
node_key<<"SHARD-"<<i<<"-NODE-"<<j;
uint32_t partition = murmur3_32(node_key.str().c_str(), strlen(node_key.str().c_str()));
server_nodes_.insert(pair<uint32_t, size_t>(partition, i));
}
}
}
size_t ConsistentHash::GetServerIndex(const char* key)
{
uint32_t partition = murmur3_32(key, strlen(key));
map<uint32_t, size_t>::iterator it = server_nodes_.lower_bound(partition);//沿環的順時針找到一個大於等於key的虛擬節點
if(it == server_nodes_.end())//未找到
{
return server_nodes_.begin()->second;
}
return it->second;
}
void ConsistentHash::DeleteNode(const int index)
{
for(int j=0; j<virtual_node_num_; ++j)
{
stringstream node_key;
node_key<<"SHARD-"<<index<<"-NODE-"<<j;
uint32_t partition = murmur3_32(node_key.str().c_str(), strlen(node_key.str().c_str()));
map<uint32_t,size_t>::iterator it = server_nodes_.find(partition);
if(it != server_nodes_.end())
{
server_nodes_.erase(it);
}
}
}
void ConsistentHash::AddNewNode(const int index)
{
for(int j=0; j<virtual_node_num_; ++j)
{
stringstream node_key;
node_key<<"SHARD-"<<index<<"-NODE-"<<j;
uint32_t partition = murmur3_32(node_key.str().c_str(), strlen(node_key.str().c_str()));
server_nodes_.insert(pair<uint32_t, size_t>(partition, index));
}
}四. 測試結果
假設有10000個樣本,10種測試值(0-9)。
一致性雜湊中真實節點有5個(index是0-4),每個節點關聯100個虛擬節點。
測試結果如下:
consistent hash initialize success, node_num=5, virtual_num=100
key = 4, index = 3
key = 7, index = 3
key = 0, index = 3
key = 1, index = 3
key = 6, index = 3
key = 3, index = 3
key = 5, index = 0
key = 2, index = 4
key = 8, index = 2
key = 9, index = 0
node error,index = 3
key = 3, index = 4
key = 7, index = 2
key = 4, index = 1
key = 0, index = 2
key = 1, index = 1
key = 6, index = 4
node recover,index = 3
key = 4, index = 3
key = 3, index = 3
key = 0, index = 3
key = 1, index = 3
key = 7, index = 3
key = 6, index = 3
index = 0, data_count = 5985
index = 1, data_count = 1991
index = 2, data_count = 5041
index = 3, data_count = 12014
index = 4, data_count = 4969測試了3次,每次10000個樣本;
第二次測試時,節點3壞了,導致原來儲存在節點3的資料(0,1,3,4,6,7)都被分配到了其他節點,但並不是全部都到某個節點上,防止了雪崩;
第三次測試時,節點3恢復了,原來在節點3上的資料又恢復到3上了。