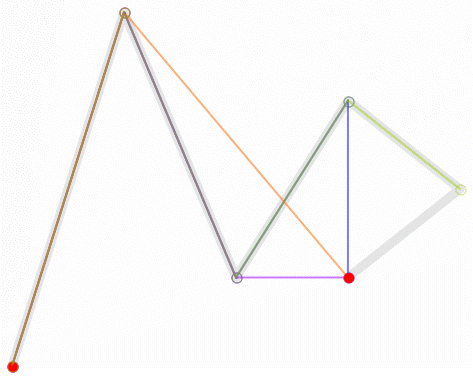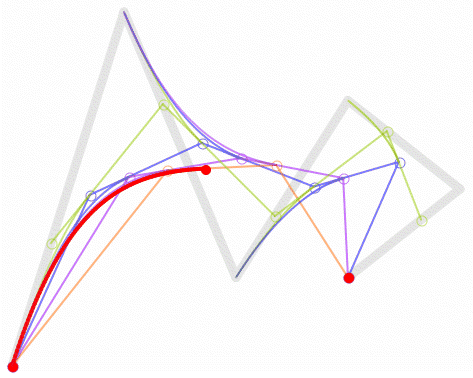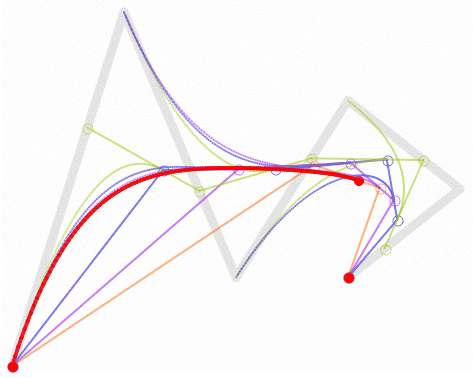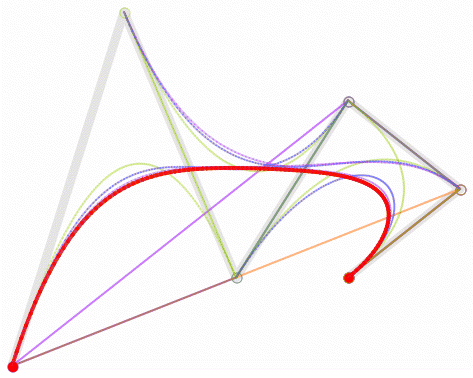
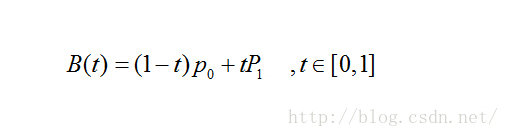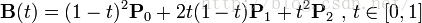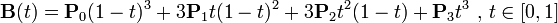Android自定義控制元件-Path之貝賽爾曲線和手勢軌跡、水波紋效果
從這篇開始,我將延續androidGraphics系列文章把圖片相關的知識給大家講完,這一篇先稍微進階一下,給大家把《android Graphics(二):路徑及文字》略去的quadTo(二階貝塞爾)函式,給大家補充一下。
本篇最終將以兩個例子給大家演示貝塞爾曲線的強大用途:
1、手勢軌跡

利用貝塞爾曲線,我們能實現平滑的手勢軌跡效果
2、水波紋效果
電池充電時,有些手機會顯示水波紋效果,就是這樣做出來的。
廢話不多說,開整吧
一、概述
在《android Graphics(二):路徑及文字》中我們略去了有關所有貝賽爾曲線的知識,在Path中有四個函式與貝賽爾曲線有關:
- //二階貝賽爾
- publicvoid quadTo(float x1, float y1, float x2, float y2)
- publicvoid rQuadTo(float dx1, float dy1, float dx2, float dy2)
- //三階貝賽爾
- publicvoid cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
- publicvoid rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
1、貝賽爾曲線來源
在數學的數值分析領域中,貝賽爾曲線(Bézier曲線)是電腦圖形學中相當重要的引數曲線。更高維度的廣泛化貝塞爾曲線就稱作貝塞爾曲面,其中貝塞爾三角是一種特殊的例項。
貝塞爾曲線於1962年,由法國工程師皮埃爾·貝塞爾(Pierre Bézier)所廣泛發表,他運用貝塞爾曲線來為汽車的主體進行設計。貝塞爾曲線最初由Paul de Casteljau於1959年運用de Casteljau演算法開發,以穩定數值的方法求出貝塞爾曲線。
2、貝賽爾曲線公式
這部分是很有難度的,大家做好準備了哦
一階貝賽爾曲線
其公式可概括為:
對應動畫演示為:
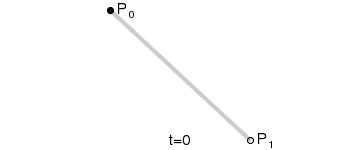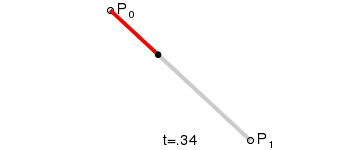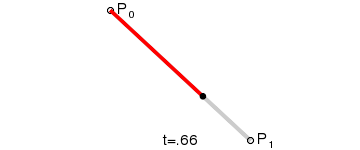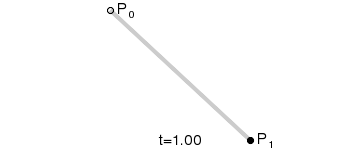
P0為起點、P1為終點,t表示當前時間,B(t)表示公式的結果值。
注意,曲線的意義就是公式結果B(t)隨時間的變化,其取值所形成的軌跡。在動畫中,黑色點表示在當前時間t下公式B(t)的取值。而紅色的那條線就不在各個時間點下不同取值的B(t)所形成的軌跡。
總而言之:對於一階貝賽爾曲線,大家可以理解為在起始點和終點形成的這條直線上,勻速移動的點。
二階貝賽爾曲線
同樣,先來看看二階貝賽爾曲線的公式(雖然看不懂,呵呵)
大家也不用研究這個公式了,沒一定數學功底也研究不出來了啥,咱還是看動畫吧
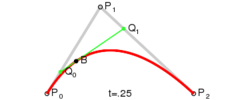
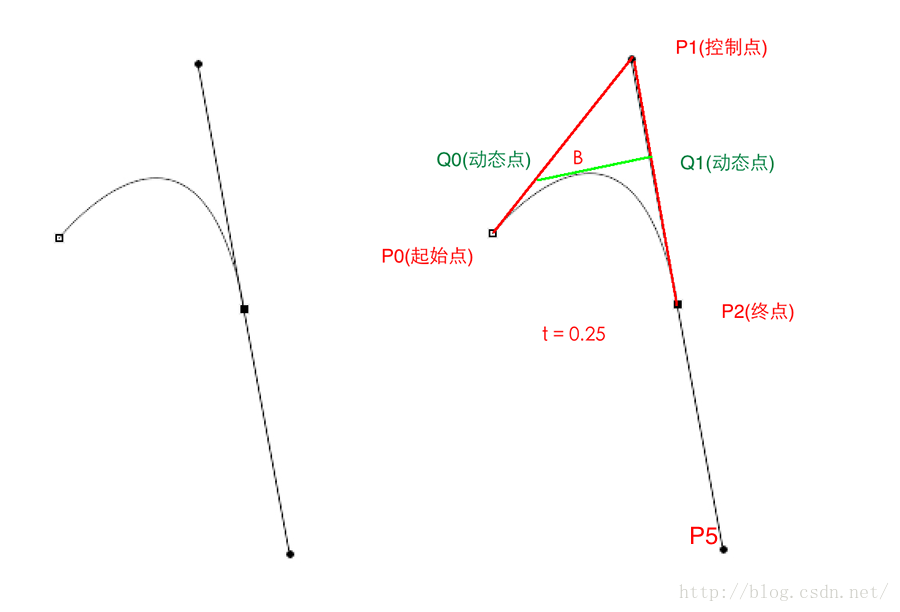
在這裡P0是起始點,P2是終點,P1是控制點
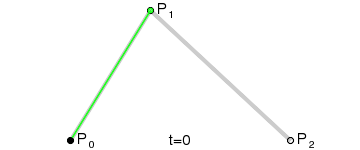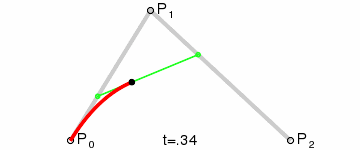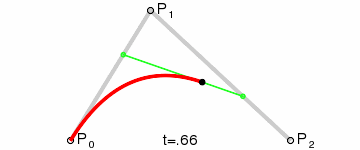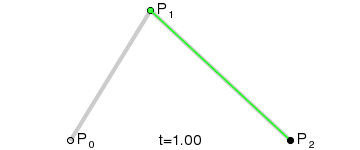
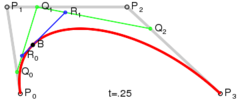
假設將時間定在t=0.25的時刻,此時的狀態如下圖所示:
首先,P0點和P1點形成了一條貝賽爾曲線,還記得我們上面對一階貝賽爾曲線的總結麼:就是一個點在這條直線上做勻速運動;所以P0-P1這條直線上的移動的點就是Q0;
同樣,P1,P2形成了一條一階貝賽爾曲線,在這條一階貝賽爾曲線上,它們的隨時間移動的點是Q1
最後,動態點Q0和Q1又形成了一條一階貝賽爾曲線,在它們這條一階貝賽爾曲線動態移動的點是B
而B的移動軌跡就是這個二階貝賽爾曲線的最終形態。從上面的講解大家也可以知道,之所以叫它二階貝賽爾曲線是因為,B的移動軌跡是建立在兩個一階貝賽爾曲線的中間點Q0,Q1的基礎上的。
在理解了二階貝賽爾曲線的形成原理以後,我們就不難理解三階貝賽爾曲線了
三階貝賽爾曲線
同樣,先列下基本看不懂的公式
這玩意估計也看不懂,講了也沒什麼意義,還是結合動畫來吧
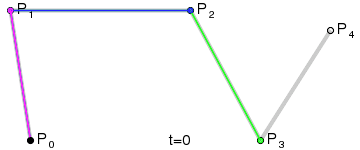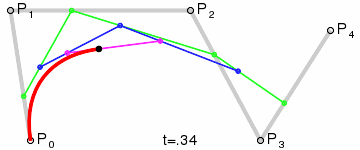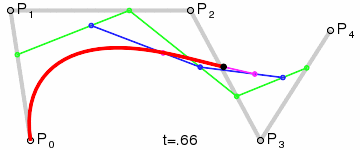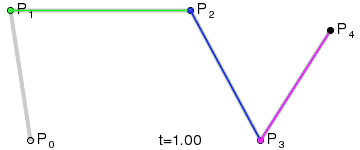
同樣,我們取其中一點來講解軌跡的形成原理,當t=0.25時,此時狀態如下:
同樣,P0是起始點,P3是終點;P1是第一個控制點,P2是第二個控制點;
首先,這裡有三條一階貝賽爾曲線,分別是P0-P1,P1-P2,P2-P3;
他們隨時間變化的點分別為Q0,Q1,Q2
然後是由Q0,Q1,Q2這三個點,再次連線,形成了兩條一階貝賽爾曲線,分別是Q0—Q1,Q1—Q2;他們隨時間變化的點為R0,R1
同樣,R0和R1同樣可以連線形成一條一階貝賽爾曲線,在R0—R1這條貝賽爾曲線上隨時間移動的點是B
而B的移動軌跡就是這個三階貝賽爾曲線的最終形狀。
從上面的解析大家可以看出,所謂幾階貝賽爾曲線,全部是由一條條一階貝賽爾曲線搭起來的;
在上圖中,形成一階貝賽爾曲線的直線是灰色的,形成二階貝賽爾曲線線是綠色的,形成三階貝賽爾曲線的線是藍色的。
在理解了上面的二階和三階貝賽爾曲線以後,我們再來看幾個貝賽爾曲線的動態圖
四階貝賽爾曲線
五階貝賽爾曲線
這裡就不再一一講解形成原理了,大家理解了二階和三階貝賽爾曲線以後,這兩條的看看就好了,想必大家也是能自己推出四階貝賽爾曲線的形成原理的。
3、貝賽爾曲線與PhotoShop鋼筆工具
如果有些同學不懂PhotoShop,這篇文章可能就會有些難度了,本篇文章主要是利用PhotoShop的鋼筆工具來得出具體貝塞爾影象的
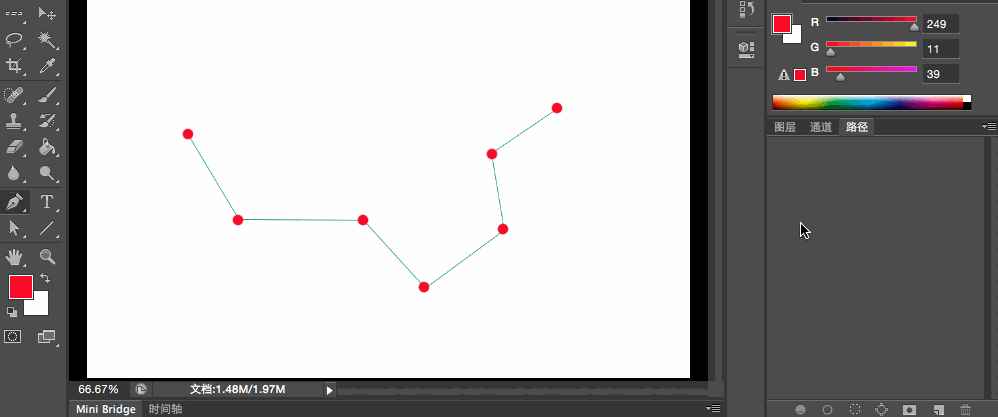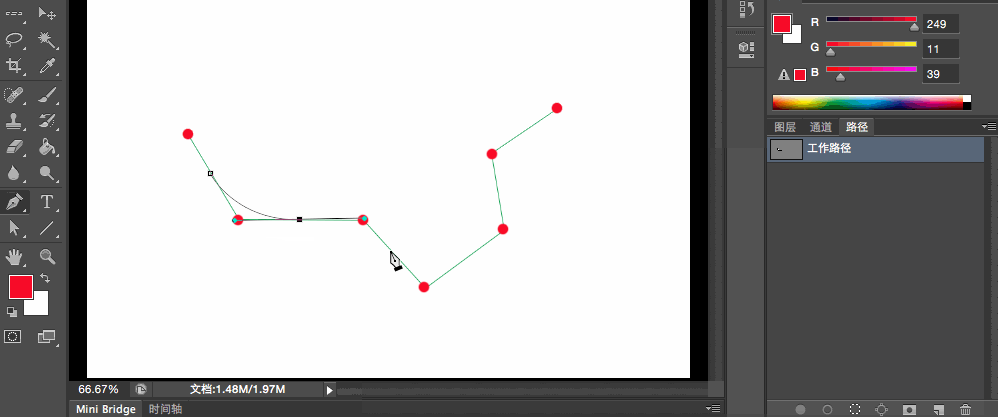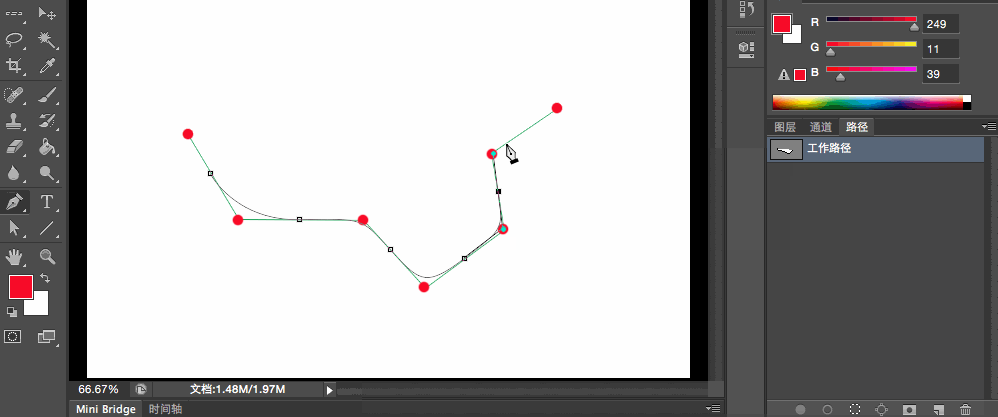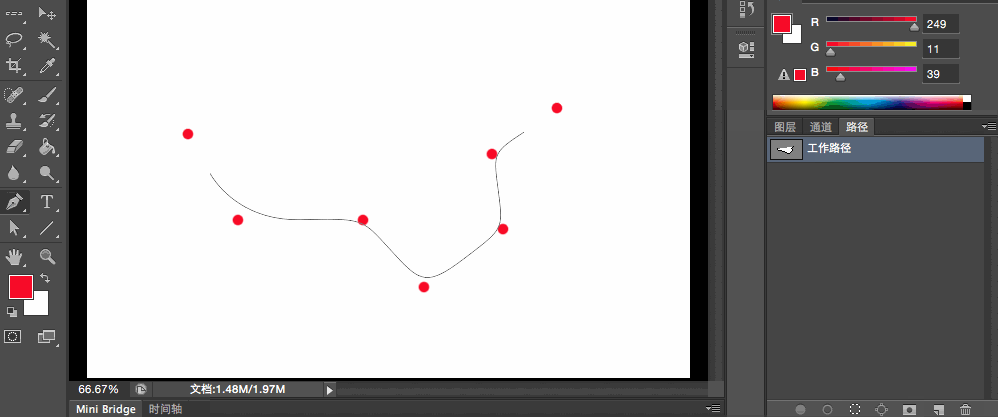
這麼屌的貝賽爾曲線,在專業繪圖工具PhotoShop中當然會有它的蹤影,它就是鋼筆工具,鋼筆工具所使用的路徑彎曲效果就是二階貝賽爾曲線。
我來給大家演示一下鋼筆工具的用法:
我們拿最終成形的圖形來看一下為什麼鋼筆工具是二階貝賽爾曲線:
右圖演示的假設某一點t=0.25時,動態點B的位置圖
同樣,這裡P0是起始點,P2是終點,P1是控制點;
P0-P1、P1-P2形成了第一層的一階貝賽爾曲線。它們隨時間的動態點分別是Q0,Q1
動態點Q0,Q1又形成了第二層的一階貝賽爾曲線,它們的動態點是B.而B的軌跡跟鋼筆工具的形狀是完全一樣的。所以鋼筆工具的拉伸效果是使用的二階貝賽爾曲線!
這個圖與上面二階貝賽爾曲線t=0.25時的曲線差不多,大家理解起來難度也不大。
這裡需要注意的是,我們在使用鋼筆工具時,拖動的是P5點。其實二階貝賽爾曲線的控制點是其對面的P1點,鋼筆工具這樣設計是當然是因為操作起來比較方便。
好了,對貝賽爾曲線的知識講了那麼多,下面開始實戰了,看在程式碼中,貝賽爾曲線是怎麼來做的。
二、Android中貝賽爾曲線之quadTo
在開篇中,我們已經提到,在Path類中有四個方法與貝賽爾曲線相關,分別是:
- //二階貝賽爾
- publicvoid quadTo(float x1, float y1, float x2, float y2)
- publicvoid rQuadTo(float dx1, float dy1, float dx2, float dy2)
- //三階貝賽爾
- publicvoid cubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
- publicvoid rCubicTo(float x1, float y1, float x2, float y2,float x3, float y3)
1、quadTo使用原理
這部分我們先來看看quadTo函式的用法,其定義如下:
- publicvoid quadTo(float x1, float y1, float x2, float y2)
大家可能會有一個疑問:有控制點和終點座標,那起始點是多少呢?
整條線的起始點是通過Path.moveTo(x,y)來指定的,而如果我們連續呼叫quadTo(),前一個quadTo()的終點,就是下一個quadTo()函式的起點;如果初始沒有呼叫Path.moveTo(x,y)來指定起始點,則預設以控制元件左上角(0,0)為起始點;大家可能還是有點迷糊,下面我們就舉個例子來看看
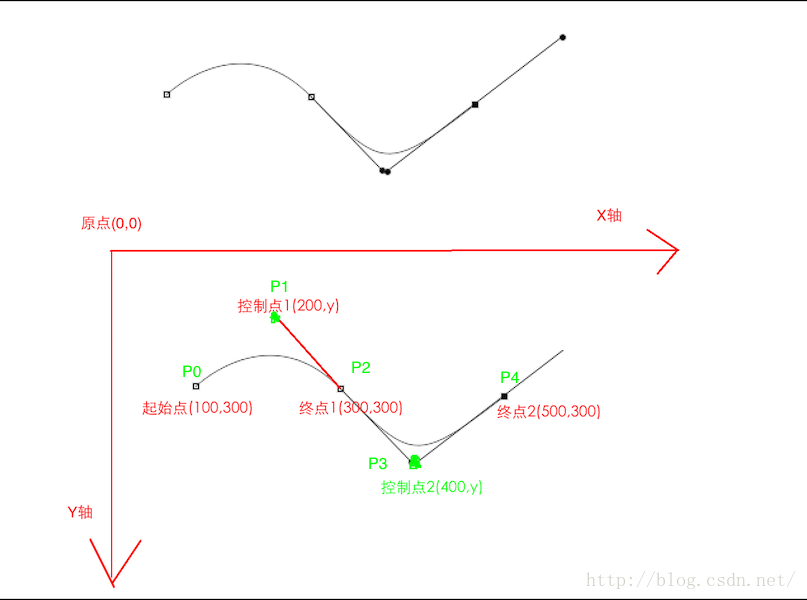
我們利用quadTo()來畫下面的這條波浪線:
最關鍵的是如何來確定控制點的位置!前面講過,PhotoShop中的鋼筆工具是二階貝賽爾曲線,所以我們可以利用鋼筆工具來模擬畫出這條波浪線來輔助確定控制點的位置
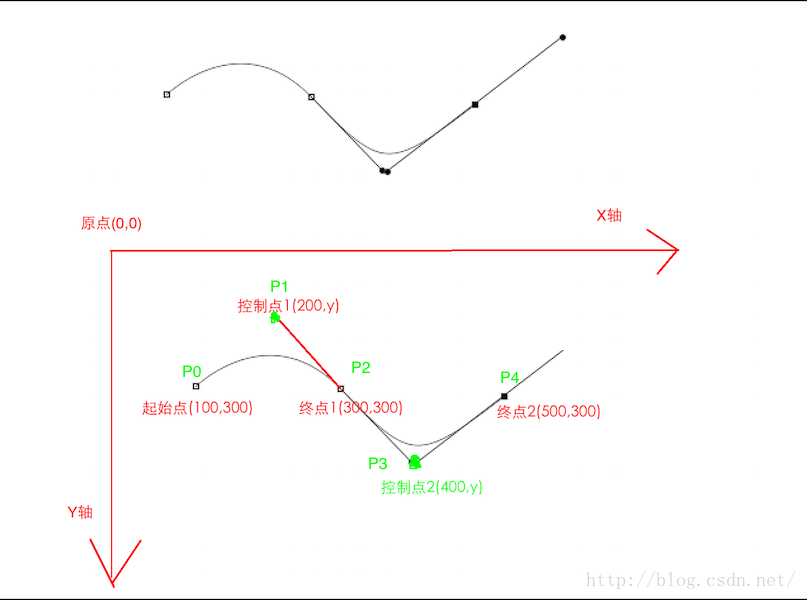
下面我們來看看這個路徑軌跡中,控制點分別在哪個位置
我們先看P0-P2這條軌跡,P0是起點,假設位置座標是(100,300),P2是終點,假充位置座標是(300,300);在以P0為起始點,P2為終點這條二階貝賽爾曲線上,P1是控制點,很明顯P1大概在P0,P2中間的位置,所以它的X座標應該是200,關於Y座標,我們無法確定,但很明顯的是P1在P0,P2點的上方,也就是它的Y值比它們的小,所以根據鋼筆工具上面的位置,我們讓P1的比P0,P2的小100;所以P1的座標是(200,200)
同理,不難求出在P2,P4這條二階貝賽爾曲線上,它們的控制點P3的座標位置應該是(400,400);P3的X座標是400是,因為P3點是P2,P4的中間點;與P3與P1距離P0-P2-P4這條直線的距離應該是相等的。P1距離P0-P2的值為100;P3距離P2-P4的距離也應該是100,這樣不難算出P3的座標應該是(400,400);
下面開始是程式碼部分了。
2、示例程式碼
(1)、自定義View
我們知道在動畫繪圖時,會呼叫onDraw(Canvas canvas)函式,我們如果重寫了onDraw(Canvas canvas)函式,那麼我們利用canvas在上面畫了什麼,就會顯示什麼。所以我們自定義一個View
- publicclass MyView extends View {
- public MyView(Context context) {
- super(context);
- }
- public MyView(Context context, AttributeSet attrs) {
- super(context, attrs);
- }
- @Override
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setStyle(Paint.Style.STROKE);
- paint.setColor(Color.GREEN);
- Path path = new Path();
- path.moveTo(100,300);
- path.quadTo(200,200,300,300);
- path.quadTo(400,400,500,300);
- canvas.drawPath(path,paint);
- }
- }
所以,大家在自定義控制元件的時候,要多跟UED溝通,看他們是如何來實現這個效果的,如果是用的鋼筆工具,那我們也可以效仿使用二階貝賽爾曲線來實現。
2、使用MyView
在自定義控制元件以後,然後直接把它引入到主佈局檔案中即可(main.xml)
- <?xmlversion="1.0"encoding="utf-8"?>
- <LinearLayoutxmlns:android="http://schemas.android.com/apk/res/android"
- android:orientation="vertical"
- android:layout_width="fill_parent"
- android:layout_height="fill_parent">
- <com.harvic.BlogBerzMovePath.MyView
- android:layout_width="match_parent"
- android:layout_height="match_parent"/>
- </LinearLayout>
- publicclass MyActivity extends Activity {
- /**
- * Called when the activity is first created.
- */
- @Override
- publicvoid onCreate(Bundle savedInstanceState) {
- super.onCreate(savedInstanceState);
- setContentView(R.layout.main);
- }
- }
通過這個例子希望大家知道兩點:
- 整條線的起始點是通過Path.moveTo(x,y)來指定的,如果初始沒有呼叫Path.moveTo(x,y)來指定起始點,則預設以控制元件左上角(0,0)為起始點;
- 而如果我們連續呼叫quadTo(),前一個quadTo()的終點,就是下一個quadTo()函式的起點;
三、手指軌跡
要實現手指軌跡其實是非常簡單的,我們只需要在自定義中攔截OnTouchEvent,然後根據手指的移動軌跡來繪製Path即可。
要實現把手指的移動軌跡連線起來,最簡單的方法就是直接使用Path.lineTo()就能實現把各個點連線起來。
1、實現方式一:Path.lineTo(x,y)
我們先來看看效果圖:
(1)、自定義View——MyView
首先,我們自定義一個View,完整程式碼如下:
- publicclass MyView extends View {
- private Path mPath = new Path();
- public MyView(Context context) {
- super(context);
- }
- public MyView(Context context, AttributeSet attrs) {
- super(context, attrs);
- }
- @Override
- publicboolean onTouchEvent(MotionEvent event) {
- switch (event.getAction()){
- case MotionEvent.ACTION_DOWN: {
- mPath.moveTo(event.getX(), event.getY());
- returntrue;
- }
- case MotionEvent.ACTION_MOVE:
- mPath.lineTo(event.getX(), event.getY());
- postInvalidate();
- break;
- default:
- break;
- }
- returnsuper.onTouchEvent(event);
- }
- @Override
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setColor(Color.GREEN);
- paint.setStyle(Paint.Style.STROKE);
- canvas.drawPath(mPath,paint);
- }
- publicvoid reset(){
- mPath.reset();
- invalidate();
- }
- }
- publicboolean onTouchEvent(MotionEvent event) {
- switch (event.getAction()){
- case MotionEvent.ACTION_DOWN: {
- mPath.moveTo(event.getX(), event.getY());
- returntrue;
- }
- case MotionEvent.ACTION_MOVE:
- mPath.lineTo(event.getX(), event.getY());
- postInvalidate();
- break;
- default:
- break;
- }
- returnsuper.onTouchEvent(event);
- }
Path.moveTo()和Path.lineTo()的用法,大家如果看了《android Graphics(二):路徑及文字》之後,理解起來應該沒什麼難度,但這裡有兩個地方需要注意
第一:有關在case MotionEvent.ACTION_DOWN時return true的問題:return true表示當前控制元件已經消費了下按動作,之後的ACTION_MOVE、ACTION_UP動作也會繼續傳遞到當前控制元件中;如果我們在case MotionEvent.ACTION_DOWN時return false,那麼後序的ACTION_MOVE、ACTION_UP動作就不會再傳到這個控制元件來了。有關動作攔截的知識,後續會在這個系列中單獨來講,大家先期待下吧。
第二:這裡重繪控制元件使用的是postInvalidate();而我們以前也有用Invalidate()函式的。這兩個函式的作用都是用來重繪控制元件的,但區別是Invalidate()一定要在UI執行緒執行,如果不是在UI執行緒就會報錯。而postInvalidate()則沒有那麼多講究,它可以在任何執行緒中執行,而不必一定要是主執行緒。其實在postInvalidate()就是利用handler給主執行緒傳送重新整理介面的訊息來實現的,所以它是可以在任何執行緒中執行,而不會出錯。而正是因為它是通過發訊息來實現的,所以它的介面重新整理可能沒有直接調Invalidate()刷的那麼快。
所以在我們確定當前執行緒是主執行緒的情況下,還是以invalide()函式為主。當我們不確定當前要重新整理頁面的位置所處的執行緒是不是主執行緒的時候,還是用postInvalidate為好;
這裡我是故意用的postInvalidate(),因為onTouchEvent()本來就是在主執行緒中的,使用Invalidate()是更合適的。當我們
有關OnDraw函式就沒什麼好講的,就是把path給畫出來:
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setColor(Color.GREEN);
- paint.setStyle(Paint.Style.STROKE);
- canvas.drawPath(mPath,paint);
- }
- publicvoid reset(){
- mPath.reset();
- invalidate();
- }
(2)、主佈局
然後看看佈局檔案(mian.xml)
- <?xmlversion="1.0"encoding="utf-8"?>
- <LinearLayoutxmlns:android="http://schemas.android.com/apk/res/android"
- android:orientation="vertical"
- android:layout_width="fill_parent"
- android:layout_height="fill_parent">
- <Button
- android:id="@+id/reset"
- android:layout_width="match_parent"
- android:layout_height="wrap_content"
- android:text="reset"/>
- <com.harvic.BlogMovePath.MyView
- android:id="@+id/myview"
- android:layout_width="match_parent"
- android:layout_height="match_parent"/>
- </LinearLayout>
(3)、MyActivity
然後看MyActivity的操作:
- publicclass MyActivity extends Activity {
- @Override
- publicvoid onCreate(Bundle savedInstanceState) {
- super.onCreate(savedInstanceState);
- setContentView(R.layout.main);
- final MyView myView = (MyView)findViewById(R.id.myview);
- findViewById(R.id.reset).setOnClickListener(new View.OnClickListener() {
- @Override
- publicvoid onClick(View v) {
- myView.reset();
- }
- });
- }
- }
原始碼在文章底部給出
(4)、使用Path.lineTo()所存在問題
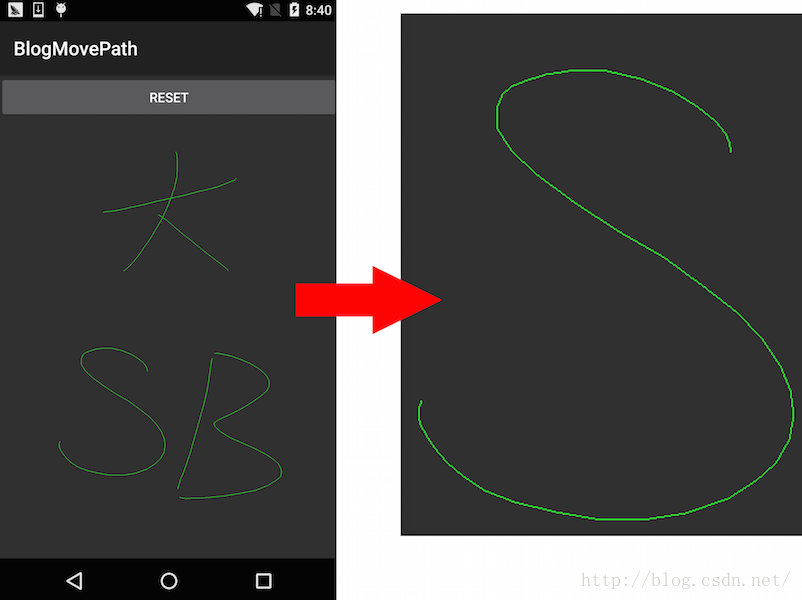
上面我們雖然實現了,畫出手指的移動軌跡,但我們仔細來看看畫出來的圖:
我們把S放大,明顯看出,在兩個點連線處有明顯的轉折,而且在S頂部位置橫縱座標變化比較快的位置,看起來跟圖片這大後的馬賽克一樣;利用Path繪圖,是不可能出現馬賽克的,因為除了Bitmap以外的任何canvas繪圖全部都是向量圖,也就是利用數學公式來作出來的圖,無論放在多大螢幕上,都不可能會出現馬賽克!這裡利用Path繪圖,在S頂部之所以看起來像是馬賽克是因為這個S是由各個不同點之間連線寫出來的,而之間並沒有平滑過渡,所以當座標變化比較劇烈時,線與線之間的轉折就顯得特別明顯了。
所以要想優化這種效果,就得實現線與線之間的平滑過渡,很顯然,二階貝賽爾曲線就是幹這個事的。下面我們就利用我們新學的Path.quadTo函式來重新實現下移動軌跡效果。
2、實現方式二(優化):使用Path.quadTo()函式實現過渡
(1)、原理概述
我們上面講了,使用Path.lineTo()的最大問題就是線段轉折處不夠平滑。Path.quadTo()可以實現平滑過渡,但使用Path.quadTo()的最大問題是,如何找到起始點和結束點。
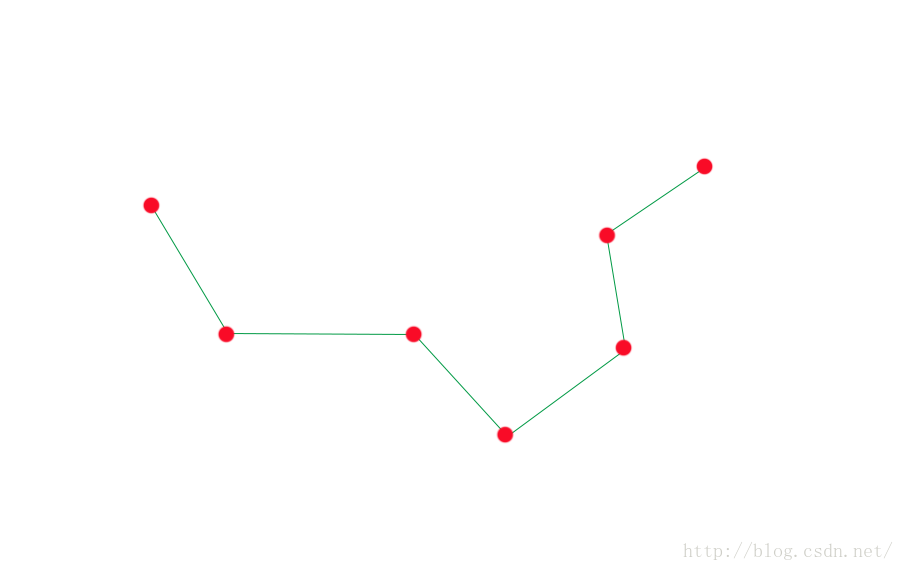
下圖中,有用綠點表示的三個點,連成的兩條直線,很明顯他們轉折處是有明顯摺痕的
下面我們在PhotoShop中利用鋼筆工具,看如何才能實現這兩條線之間的轉折
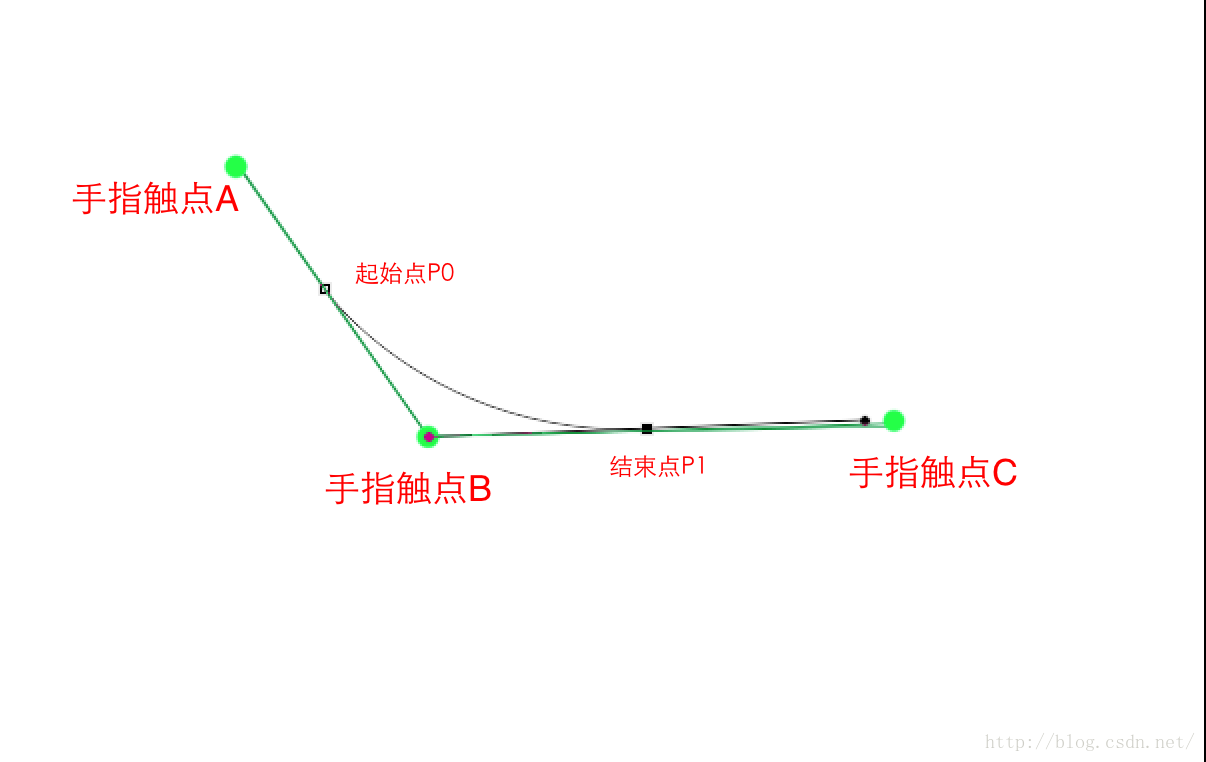
從這兩個線段中可以看出,我們使用Path.lineTo()的時候,是直接把手指觸點A,B,C給連起來。
而鋼筆工具要實現這三個點間的流暢過渡,就只能將這兩個線段的中間點做為起始點和結束點,而將手指的倒數第二個觸點B做為控制點。
大家可能會覺得,那這樣,在結束的時候,A到P0和P1到C1的這段距離豈不是沒畫進去?是的,如果Path最終沒有close的話,這兩段距離是被拋棄掉的。因為手指間滑動時,每兩個點間的距離很小,所以P1到C之間的距離可以忽略不計。
下面我們就利用這種方法在photoshop中求證,在連線多個線段時,是否能行?
在這個圖形中,有很多點連成了彎彎曲曲的線段,我們利用上面我們講的,將兩個線段的中間做為二階貝爾賽曲線的起始點和終點,把上一個手指的位置做為控制點,來看看是否真的能組成平滑的連線
整個連線過程如動畫所示:
在最終的路徑中看來,各個點間的連線是非常平滑的。從這裡也可以看出,在為了實現平滑效果,我們只能把開頭的線段一半和結束的線段的一半拋棄掉。
在講了原理之後,下面就來看看在程式碼中如何來實現吧。
(2)、自定義View
先貼出完整程式碼然後再細講:
- publicclass MyView extends View {
- private Path mPath = new Path();
- privatefloat mPreX,mPreY;
- public MyView(Context context) {
- super(context);
- }
- public MyView(Context context, AttributeSet attrs) {
- super(context, attrs);
- }
- @Override
- publicboolean onTouchEvent(MotionEvent event) {
- switch (event.getAction()){
- case MotionEvent.ACTION_DOWN:{
- mPath.moveTo(event.getX(),event.getY());
- mPreX = event.getX();
- mPreY = event.getY();
- returntrue;
- }
- case MotionEvent.ACTION_MOVE:{
- float endX = (mPreX+event.getX())/2;
- float endY = (mPreY+event.getY())/2;
- mPath.quadTo(mPreX,mPreY,endX,endY);
- mPreX = event.getX();
- mPreY =event.getY();
- invalidate();
- }
- break;
- default:
- break;
- }
- returnsuper.onTouchEvent(event);
- }
- @Override
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setStyle(Paint.Style.STROKE);
- paint.setColor(Color.GREEN);
- paint.setStrokeWidth(2);
- canvas.drawPath(mPath,paint);
- }
- publicvoid reset(){
- mPath.reset();
- postInvalidate();
- }
- }
- publicboolean onTouchEvent(MotionEvent event) {
- switch (event.getAction()){
- case MotionEvent.ACTION_DOWN:{
- mPath.moveTo(event.getX(),event.getY());
- mPreX = event.getX();
- mPreY = event.getY();
- returntrue;
- }
- …………
- }
- returnsuper.onTouchEvent(event);
- }
在ACTION_MOVE時:
- case MotionEvent.ACTION_MOVE:{
- float endX = (mPreX+event.getX())/2;
- float endY = (mPreY+event.getY())/2;
- mPath.quadTo(mPreX,mPreY,endX,endY);
- mPreX = event.getX();
- mPreY =event.getY();
- invalidate();
- }
所以這裡的起始點,就是上一個線段的中間點。所以,這樣就與鋼筆工具繪製過程完全對上了:把各個線段的中間點做為起始點和終點,把終點前一個手指位置做為控制點。
後面的onDraw()和reset()函式就沒什麼難度了,上面的例子中也講過了,就不再贅述了
最終的效果圖如下:

同樣把lineTo和quadTo實現的S拿來對比下:

從效果圖中可以明顯可以看出,通過quadTo實現的曲線更順滑
原始碼在文章底部給出
Ok啦,quadeTo的用法,到這裡就結束了,下部分再來講講rQuadTo的用法及波浪動畫效果
四、Path.rQuadTo()
1、概述
該函式宣告如下
- publicvoid rQuadTo(float dx1, float dy1, float dx2, float dy2)
- dx1:控制點X座標,表示相對上一個終點X座標的位移座標,可為負值,正值表示相加,負值表示相減;
- dy1:控制點Y座標,相對上一個終點Y座標的位移座標。同樣可為負值,正值表示相加,負值表示相減;
- dx2:終點X座標,同樣是一個相對座標,相對上一個終點X座標的位移值,可為負值,正值表示相加,負值表示相減;
- dy2:終點Y座標,同樣是一個相對,相對上一個終點Y座標的位移值。可為負值,正值表示相加,負值表示相減;
這四個引數都是傳遞的都是相對值,相對上一個終點的位移值。
比如,我們上一個終點座標是(300,400)那麼利用rQuadTo(100,-100,200,100);
得到的控制點座標是(300+100,400-100)即(500,300)
同樣,得到的終點座標是(300+200,400+100)即(500,500)
所以下面這兩段程式碼是等價的:
利用quadTo定義絕對座標
- path.moveTo(300,400);
- path.quadTo(500,300,500,500);
- path.moveTo(300,400);
- path.rQuadTo(100,-100,200,100)
2、使用rQuadTo實現波浪線
在上篇中,我們使用quadTo實現了一個簡單的波浪線:
各個點具體計算過程,在上篇已經計算過了,下面是上篇中onDraw的程式碼:
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setStyle(Paint.Style.STROKE);
- paint.setColor(Color.GREEN);
- Path path = new Path();
- path.moveTo(100,300);
- path.quadTo(200,200,300,300);
- path.quadTo(400,400,500,300);
- canvas.drawPath(path,paint);
- }
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- Paint paint = new Paint();
- paint.setStyle(Paint.Style.STROKE);
- paint.setColor(Color.GREEN);
- Path path = new Path();
- path.moveTo(100,300);
- path.rQuadTo(100,-100,200,0);
- path.rQuadTo(100,100,200,0);
- canvas.drawPath(path,paint);
- }
- path.moveTo(100,300);
- path.quadTo(200,200,300,300);
- path.quadTo(400,400,500,300);
- path.moveTo(100,300);
- path.rQuadTo(100,-100,200,0);
- path.rQuadTo(100,100,200,0);
所以
控制點X座標=上一個終點X座標+控制點X位移 = 100+100=200;
控制點Y座標=上一個終點Y座標+控制點Y位移 = 300-100=200;
終點X座標 = 上一個終點X座標+終點X位移 = 100+200=300;
終點Y座標 = 上一個終點Y座標+控制點Y位移 = 300+0=300;
所以這句與path.quadTo(200,200,300,300);對等的
第二句:path.rQuadTo(100,100,200,0);是建立在它的前一個終點即(300,300)的基礎上來計算相對座標的!
所以
控制點X座標=上一個終點X座標+控制點X位移 = 300+100=200;
控制點Y座標=上一個終點Y座標+控制點Y位移 = 300+100=200;
終點X座標 = 上一個終點X座標+終點X位移 = 300+200=500;
終點Y座標 = 上一個終點Y座標+控制點Y位移 = 300+0=300;
所以這句與path.quadTo(400,400,500,300);對等的
最終效果也是一樣的。
通過這個例子,只想讓大家明白一點:rQuadTo(float dx1, float dy1, float dx2, float dy2)中的位移座標,都是以上一個終點位置為基準來做偏移的!
五、實現波浪效果
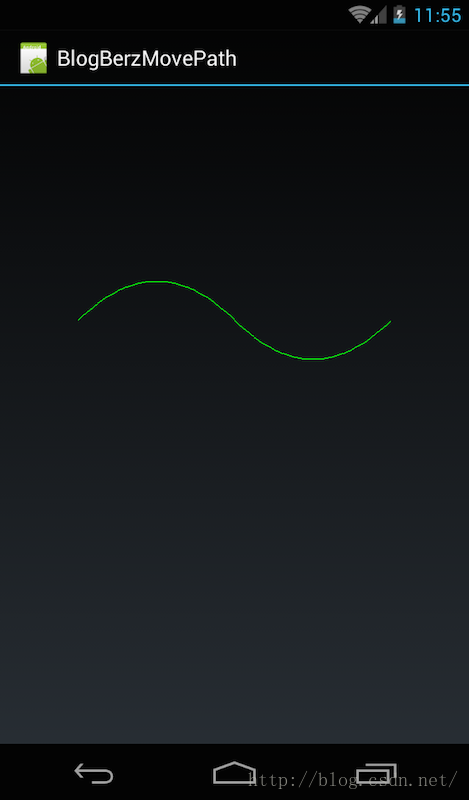
本節完成之後,將實現文章開頭的波浪效果,如下。
1、實現全屏波紋
上面我們已經能夠實現一個波形,只要我們再多實現幾個波形,就可以覆蓋整個螢幕了。
對應程式碼如下:
- publicclass MyView extends View {
- private Paint mPaint;
- private Path mPath;
- privateint mItemWaveLength = 400;
- public MyView(Context context, AttributeSet attrs) {
- super(context, attrs);
- mPath = new Path();
- mPaint = new Paint();
- mPaint.setColor(Color.GREEN);
- mPaint.setStyle(Paint.Style.STROKE);
- }
- @Override
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- mPath.reset();
- int originY = 300;
- int halfWaveLen = mItemWaveLength/2;
- mPath.moveTo(-mItemWaveLength,originY);
- for (int i = -mItemWaveLength;i<=getWidth()+mItemWaveLength;i+=mItemWaveLength){
- mPath.rQuadTo(halfWaveLen/2,-50,halfWaveLen,0);
- mPath.rQuadTo(halfWaveLen/2,50,halfWaveLen,0);
- }
- canvas.drawPath(mPath,mPaint);
- }
- }
- protectedvoid onDraw(Canvas canvas) {
- super.onDraw(canvas);
- mPath.reset();
- int originY = 300