第一章 統計學習方法概論

統計學習的主要特點是

         （1）平臺--------計算機及網路，是建立在計算機及網路之上的；
         （2）研究物件--------資料，是資料驅動的學科；
         （3）目的---------對資料進行預測與分析；
         （4）中心---------方法，統計學習方法構建模型並應用模型進行測試與分析；
         （5）交叉學科--------概率論、統計學、資訊理論、計算理論、最優化理論以及電腦科學等多個領域的交叉學科。

統計學習的物件

  面向的研究物件就是資料

統計學習方法的分類

  監督學習(supervised leaning)
  無監督學習(unsupervised leaning)
  半監督學習(semi-supervised leaning)
  強化學習(reinfoucement leaning)

統計學方法的三個要素

 統計學習方法=模型（model）+策略（strategy）+演算法（algorithm）
 模型：找到一個能夠解決問題的條件概率或者決策函式。
 策略：找到一個能夠可以優化模型（或者衡量模型的）損失函式（比如0-1損失）。
 演算法：找到一種可以優化損失函式的方法（比如：梯度下降法）。
 

統計學方法的步驟

 1  得到一個有限的訓練資料集
 2 確定假設空間（即所有可能的模型）
 3 確定選擇模型的準則（即策略）
 4 實現求解最優化模型的演算法（即演算法）
 5 選擇最優模型
 6 利用最優模型對新來的資料進行預測和分析

統計學習的研究

• 統計學習方法的研究——發現新的學習方法
• 統計學習理論的研究——提高統計學習方法的有效性和效率
• 統計學習應用的研究——-將統計學習方法應用到實際問題中去，解決實際問題。

監督學習/supervised leaning

監督學習是本書的主要學習

監督學習也可以叫做有指導的學習，（在老師的指導和監督下學習，你會學的更好）所以，一般情況下，監督學習模型要優於無監督學習模型。當然會以需要訓練集來作為代價，也就是說監督學習比無監督學習需要更多的資源（畢竟需要指導）。

假設輸入例項X的特徵向量記作
訓練集：
假設輸入變數用X表示，輸出變數用Y表示，並假設輸入與輸出的隨機變數X和Y滿足聯合概率分佈P(X,Y)，監督學習問題的模型如下所示：

這個模型還是比較容易理解的，簡單的可以理解為：將訓練集輸入到我們的學習系統—->根據決策方法學習一個最優的模型—–>利用這個最優的模型對新來的資料進行預測。

根據輸入、輸出變數的不同可以把預測任務分為以下三類：

迴歸問題-----輸入變數與輸出變數均為連續變數的預測問題；
分類問題------輸出變數為有限個離散變數的預測問題；
標註問題------輸入變數與輸出變數均為變數序列的預側問題.
他們的問題模型只需要把上圖中的“預測系統”改為“分類系統”、“標註系統”即可

三要素

模型

在監督學習過程中，模型就是所要學習的條件概率或者決策函式。
(決策函式模型)
(條件概率模型)

策略

損失函式和風險函式
損失函式(loss function)或代價函式(cost function)是用來度量模型的預測能力的。損失函式是 f (X)（預測值）和Y（真實值）之間的非負實值函式（因為兩者之間的差值可以理解為兩者之間的距離，是非負的。），記作L(Y, f (X)) 。

常用損失函式：

  (1)0-1損失函式(0-1 loss function)

 (2)平方損失函式 (quadratic loss function)

 (3)絕對損失函式 (absolute loss function)

 (4)對數損失函式(logarithmic loss function)或對數似然損失函式 (loglikehood loss function)

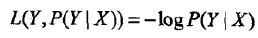
當然還存在其他的損失函式比如：指數損失函式或者Hinge Loss等。損失函式值越小，代表模型越好，模型出現的誤差越小。
經驗損失或者經驗風險
由於模型的輸入、輸出（X,Y）是隨機變數，遵循聯合分佈P(X,Y),所以損失函式的期望是：

這是理論上模型f (X)關於聯合分佈P(X,Y)的平均意義下的損失，稱為風險函式(risk function)或期望損失(expected loss)。學習的日標就是選擇期望風險最小的模型。由於，一方面根據期望風險最小化模型要用到聯合概率分佈，另一方面聯合分佈又是未知的，所以監督學習就成為一個病態問題！
在此我們提出另外一個概念：經驗風險。(根據我自己的理解，帶有“經驗”的東東，一般是平均意義下東東，畢竟經驗是需要積累的嘛。)
模型f(x)關於訓練資料集的平均損失稱為經驗風險(empirical risk)或經驗損失(empirical loss):

期望風險Rexp(f)是模型關於聯合分佈的期望損失，經驗風險Remp(f)是模型關於訓練樣本集的平均損失。根據大數定律，當樣本容量N趨於無窮時，經驗風險趨於期望風險。所以一個很自然的想法是用經驗風險估計期望風險。但是，由於現實中訓練樣本數目有限，甚至很小，所以用經驗風險估計期望風險常常並不理想，要對經驗風險進行一定的矯正.這就關係到監督學習的兩個基本策略:經驗風險最小化和結構風險最小化.

經驗風險最小化(empirical risk minimization, ERM)，即求解最優化問題：

當樣本容量足夠大時，經驗風險最小化能保證有很好的學習效果（比如一個人的經驗積累越多，判別力肯定會越好）但是當樣本容量很小的時候，經驗風險最小化的學習效果未必很好（畢竟走過的路有點小，以為世界就那麼大，所以很容易做出錯誤的判斷），可能會產生“過擬合（over-fitting）”現象。因此這時需要結構風險最小化。

結構風險最小化(structural risk minimization, SRM)是為了防止過擬合，在經驗風險上加上表示模型複雜度的正則化項(regulatizer)或罰項(penalty term )，定義是：

其中J (f)為模型的複雜度(有的時候可以理解為模型所需要的引數個數。)

結構風險小需要經驗風險與模型複雜度同時小。

演算法

學習模型的具體計算方法。統計學習問題歸結為最優化問題，統計學習的演算法成為求解最優化問
題的演算法。如何找到全域性最優解並使得求解的過程非常高效！

訓練誤差與測試誤差

一般情況下，我們將資料集分為兩大類：訓練集和測試集。（有的時候分成三部分：訓練集、驗證集、測試集）。
訓練誤差是指模型在訓練集上的誤差，反映的是模型的學習能力。
(關於訓練資料集的平均損失)
測試誤差是指模型在測試集上誤差，反映的是模型的預測能力。
(關於測試資料集的平均損失)

過擬合

過擬合(over-fitting)：如果一味追求提高對訓練資料的預側能力，所選模型的複雜度則往往會比真模型更高。這種現象稱為過擬合(over-fitting)。過擬合是指學習時選擇的模型對己知資料（訓練資料集中的資料）預測得很好，但對未知資料（測試資料集中的資料）預測得很差的現象。

例如：

上面的例子是，根據資料分佈擬合多項式模型，M代表模型的多項式次數，我們可以看到M=0和M=1的時候，模型的學習和預測能力都不好，而M=9的時候，模型的學習能力很好（幾乎都學會了，也就是說擬合出的多項式模型，可以通過每個訓練資料樣本點），但是它的預測能力很差！並且模型太複雜！而當M=3的時候，模型的學習能力和預測能力都是比較好的。（從圖影象上直觀的看到是，預測出的曲線模型和真實的曲線模型之間擬合度）。

訓練誤差和測試誤差與模型複雜度之間的關係

模型的選擇方法：正則化和交叉驗證

正則化我們學過了，就是結構風險最小化策略的實現：

上式中的第二項就是我們的正則項（或者罰項）。

交叉驗證：重複地使用資料，把給定的資料進行切分，將切分的資料集組合為訓練集與測試集，在此基礎上反覆地進行訓練、測試以及模型選擇.

簡單交叉驗證 
    首先隨機地將己給資料分為兩部分，一部分作為訓練集，另一部分作為測試集；然後用訓練集在各種條件下(例如，不同的引數個數)訓練模型，從而得到不同的模型；在測試集上評價各個模型的測試誤差，選出測試誤差最小的模型.
 k-折交叉臉證(S-fold cross validation）
     方法如下:首先隨機地將已給資料切分為S個互不相交的大小相同的子集；然後利用S-1個子集的資料訓練模型，利用餘下的子集測試模型；將這一過程對可能的S種選擇重複進行；最後選出S次評測中平均側試誤差最小的模型.
 留一文叉驗證 (leave-one-out cross validation)
     k-折交叉驗證的特殊情形是k=N，N是給定資料集的容量。

生成模型和判別模型

監督學習方法又可以分為生成方法(generative approach)和判別方法(discriminative approach).所學到的模型分別稱為生成模型(geuemtive model)和判別模型(discriminative model)。生成方法由資料學習聯合概率分佈P(X,Y),然後求出條件概率分佈P(YIX)作為預測的模型，即生成模型。

這樣的方法之所以稱為生成方法，是因為模型表示了給定輸入X產生輸出Y的生成關係.典型的生成模型有:樸素貝葉斯法和隱馬爾可夫模型。

判別方法由資料直接學習決策函式f(X)或者條件概率分佈P(Y|X)作為預測的模型，即判別模型.判別方法關心的是對給定的輸入X，應該預測什麼樣的輸出Y.典型的判別模型包括k近鄰法、感知機、決策樹、邏輯斯諦迴歸模型、最大嫡模型、支援向量機、提升方法和條件隨機場等。

給定輸入X,生成模型不能直接預測出輸出的y，需要計算之後，再比較（或者求出的是各種輸出可能性的概率值，最大作為最終的求解結果），而判別模型可以直接給出預測結果y,（利用判斷規則或者方法）

生成方法的特點：

  1、生成方法可以還原出聯合概率分佈P(X,Y)，而判別方法則不能；
 2、生成方法的學習收斂速度更快，即當樣本容量增加的時候，學到的模型可以更快地收斂於真實模型；
3、當存在隱變數時，仍可以用生成方法學習，此時判別方法就不能用。

判別方法的特點：

1、直接學習的是條件概率P(Y|X)或決策函式f(X)，直接面對預測，往往學習的準確率更高；
2、由於直接學習P(Y|X)或f(X)，可以對資料進行各種程度上的抽象、定義特徵並使用特徵，因此可以簡化學習問題.

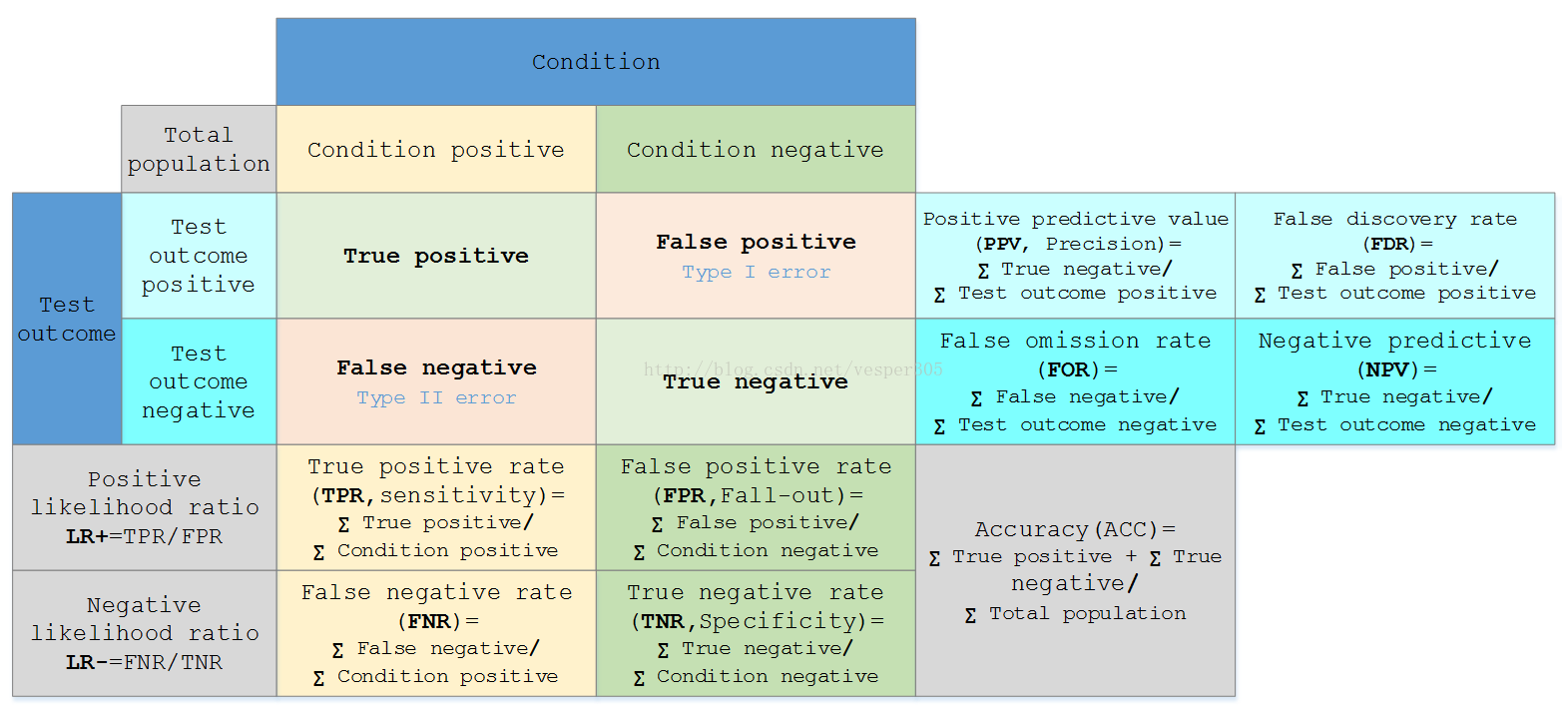
幾種模型評估標準

TP(True Positive)——將正類預測為正類數(d);
FN(False Negative)——將正類預測為負類數(c);
FP(False Positive)——將負類預測為正類數(b):
TN(True Negative)——將負類預測為負類數(a).

精確率 P(Positive)=TP/(TP+FP)=d/(d+b)
召回率R（Positive）=TP/(TP+FN)=d/(d+c)
F1（精確率和召回率的調和均值）
F1(Positive)=(2*P*R)/(P+R)

同理可以求得P(Negative)、R(Negative)、F1(Negative)
這三種度量一般用於檢測模型對每一類別的檢測或預測能力。
對模型整體評估如有準確率AC（accuracy）
AC=(a+d)/(a+b+c+d)(對角線元素，正類和負類都預測正確的樣本數)/(樣本總數)
還有ROC曲線等。
最後貼一張比較高大上的圖片，看不懂的童鞋不用較真，能準確理解上面的幾種度量標準也ok~~~

                                                          人生如棋，落子無悔
                              ----by Ada