佇列的順序儲存結構之迴圈佇列
阿新 • • 發佈:2019-01-31
佇列(queue)是隻允許在一端進行插入操作,而在另一端進行刪除操作的線性表。
佇列是一種先進先出(First In First Out)的線性表,簡稱FIFO.允許插入的一端稱為隊尾,允許刪除的一端稱為隊頭。
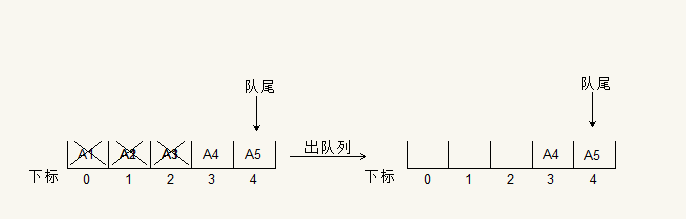
佇列的順序儲存結構使用陣列的實現,假設陣列長度為N,這時刪除隊頭元素的時候,這個元素後面的每一個元素都要移動,這樣就會出隊的效能會下降。如下圖所示:
刪除隊首的元素A1,那麼後面的其他元素都要移動到這個位置,這樣會造成出隊效能下降。
現在假設我們刪除了之後佇列中的其餘元素位置不變,是不是就可以解決了這個問題。
那樣是可以,但是又會引發新的問題,
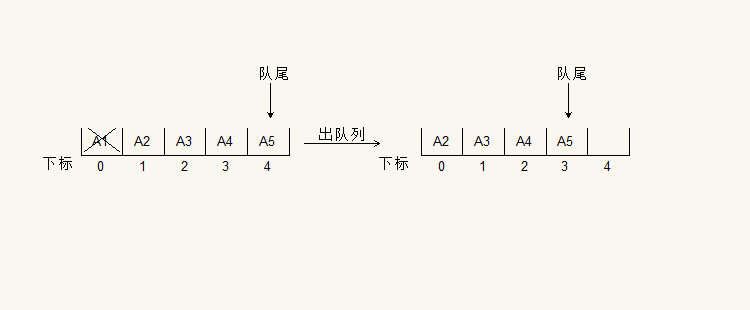
現在佇列中有5個元素已經滿了,讓A1,A2,A3都出隊,這個時候會空出3個位置,如下圖
這個時候我們同樣也是不可以在入隊了,然而佇列中還是有空間的,我們想要使用這個剩餘空間,這個時候我們是要在下標為0的位置放置元素,這樣陣列的空間就可以充分利用。這樣這個陣列就相當於一個頭尾相接的迴圈。我們把這種頭尾相接的的順序儲存結構稱為迴圈佇列。相當於下圖
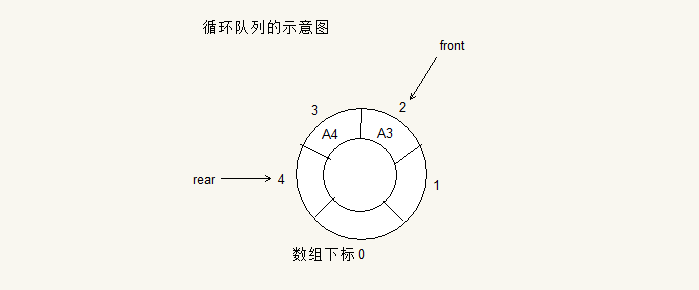
當下標為4的位置有元素,在想新增元素的時候,就放到下標為0的位置。
佇列引入了兩個指標front,rear.
front指標指向隊頭的元素,rear指標指向隊尾元素的下一個位置。
比如上圖中 A3是隊首元素 所以front指向它,A4是隊尾元素,所以rear指向它下一個位置。
假設佇列的長度為QueueSize,
那麼front和rear下一個位置的下標的分別為 (front+1)%QueueSize
佇列的長度的計算公式為: (rear-front+QueueSize)%QueueSize;
佇列為空的條件 :front ==rear
佇列滿時的條件: (rear+1)%QueueSize == front
下面是使用程式碼演示迴圈佇列的用法:
#include <stdio.h>
#define MAX_SIZE 5
typedef struct Queue
{
int data[MAX_SIZE];
int front;
int rear;
}QUEUE,*PQUEUE;
void initQueue(PQUEUE);//迴圈佇列初始化