剪枝是必須的

上一篇講了極大極小值搜尋，其實單純的極大極小值搜尋演算法並沒有實際意義。

可以做一個簡單的計算，平均一步考慮 50 種可能性的話，思考到第四層，那麼搜尋的節點數就是 50^4 = 6250000，在我的酷睿I7的電腦上一秒鐘能計算的節點不超過 5W 個，那麼 625W 個節點需要的時間在 100 秒以上。電腦一步思考 100秒肯定是不能接受的，實際上最好一步能控制在 5 秒 以內。

順便說一下層數的問題，首先思考層數必須是偶數。因為奇數節點是AI，偶數節點是玩家，如果AI下一個子不考慮玩家防守一下，那麼這個估分明顯是有問題的。
然後，至少需要進行4層思考，如果連4四層都考慮不到，那就是隻看眼前利益，那麼棋力會非常非常弱。 如果能進行6層思考基本可以達到隨便贏普通玩家的水平了（普通玩家是指沒有專門研究過五子棋的玩家，棋力大約是4層的水平）。

Alpha Beta 剪枝原理

Alpha Beta 剪枝演算法的基本依據是：棋手不會做出對自己不利的選擇。依據這個前提，如果一個節點明顯是不利於自己的節點，那麼就可以直接剪掉這個節點。

前面講到過，AI會在MAX層選擇最大節點，而玩家會在MIN層選擇最小節點。那麼如下兩種情況就是分別對雙方不利的選擇：

1. 在MAX層，假設當前層已經搜尋到一個最大值 X， 如果發現下一個節點的下一層（也就是MIN層）會產生一個比X還小的值，那麼就直接剪掉此節點。

解釋一下，也就是在MAX層的時候會把當前層已經搜尋到的最大值X存起來，如果下一個節點的下一層會產生一個比X還小的值Y，那麼之前說過玩家總是會選擇最小值的。也就是說這個節點玩家的分數不會超過Y，那麼這個節點顯然沒有必要進行計算了。

通俗點來講就是，AI發現這一步是對玩家更有利的，那麼當然不會走這一步。

1. 在MIN層，假設當前層已經搜尋到一個最小值 Y， 如果發現下一個節點的下一層（也就是MIN層）會產生一個比Y還大的值，那麼就直接剪掉此節點。

這個是一樣的道理，如果玩家走了一步棋發現其實對AI更有利，玩家必定不會走這一步。

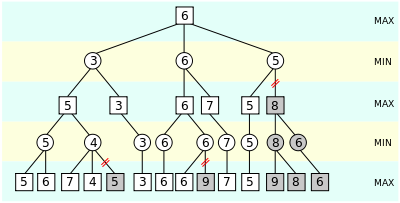
下面圖解說明，懶得畫圖，直接用wiki上的圖：

如上圖所示，在第二層，也就是MIN層，當計算到第三個節點的時候，已知前面有一個3和一個6，也就是最小值為3。 在計算第三個節點的時候，發現它的第一個孩子的結果是5，因為它的孩子是MAX節點，而MAX節點是會選擇最大值的，那麼此節點的值不會比5小，因此此節點的後序孩子就沒有必要計算了，因為這個節點不可能小於5，而同一層已經有一個值為3的節點了。

其實這個圖裡面第三層分數為7的節點也是不需要計算的。

這是 MAX 節點的剪枝，MIN節點的剪枝也是同樣的道理，就不再講了。 Alpha Beta 剪枝的 Alpha 和 Beta 分別指的是MAX 和 MIN節點。

程式碼實現

雖然原理說了很多，但是其實程式碼的實現特別簡單。

對max和min函式都增加一個 alpha 和 beta 引數。在 max 函式中如果發現一個子節點的值大於 alpha，則不再計算後序節點，此為 Alpha 剪枝。在 min 函式中如果發現一個子節點的值小於 beta，則不再計算後序節點，此為 Beta剪枝。

程式碼實現如下：

var min = function(board, deep, alpha, beta) {
  var v = evaluate(board);
  total ++;
  if(deep <= 0 || win(board)) {
    return v;
  }

  var best = MAX;
  var points = gen(board, deep);

  for(var i=0;i<points.length;i++) {
    var p = points[i];
    board[p[0]][p[1]] = R.hum;
    var v = max(board, deep-1, best < alpha ? best : alpha, beta);
    board[p[0]][p[1]] = R.empty;
    if(v < best ) {
      best = v;
    }
    if(v < beta) {  //AB剪枝
      ABcut ++;
      break;
    }
  }
  return best ;
}


var max = function(board, deep, alpha, beta) {
  var v = evaluate(board);
  total ++;
  if(deep <= 0 || win(board)) {
    return v;
  }

  var best = MIN;
  var points = gen(board, deep);

  for(var i=0;i<points.length;i++) {
    var p = points[i];
    board[p[0]][p[1]] = R.com;
    var v = min(board, deep-1, alpha, best > beta ? best : beta);
    board[p[0]][p[1]] = R.empty;
    if(v > best) {
      best = v;
    }
    if(v > alpha) { //AB 剪枝
      ABcut ++;
      break;
    }
  }
  return best;
}

優化效果

按照wiki上的說法，優化效果應該達到 1/2 次方，也就是能優化到 50^2 = 2500 左右，實際我測試的時候並沒有這麼理想。不過節點數也不到之前的十分之一，平均大約每一步計算 50W 個節點，需要時間在10秒左右。相比之前的600W節點已經有了極大的提升。

不過即使經過了Alpha Beta 剪枝，思考層數也只能達到四層，也就是一個不怎麼會玩五子棋的普通玩家的水平。而且每增加一層，所需要的時間或者說計算的節點數量是指數級增加的。所以目前的程式碼想計算到第六層是很困難的。

我們的時間複雜度是一個指數函式 M^N，其中底數M是每一層節點的子節點數，N 是思考的層數。我們的剪枝演算法能剪掉很多不用的分支，相當於減少了 N，那麼下一步我們需要減少 M，如果能把 M 減少一半，那麼四層平均思考的時間能降低到 0.5^4 = 0.06 倍，也就是能從10秒降低到1秒以內。

而這個M是怎麼來的？ 其實 M 就是函式 gen 返回的那些可選的空位。其實gen函式有很大的優化空間，而這個優化後的gen函式其實就是啟發式搜尋函式。