一、樹的相關術語

• 樹是一種非線性的資料結構，以分層的形式儲存資料
• 樹由一組以邊連線的節點組成，如下：

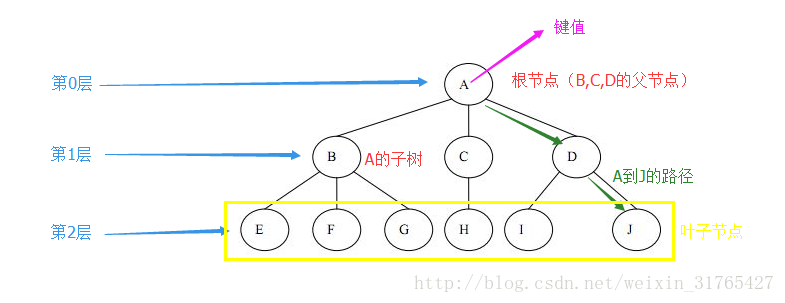
• 樹的層數被定義為樹的深度

二、二叉樹

• 二叉樹是一種特殊的樹，規定每個節點的子節點不能超過兩個
• 通過將子節點的個數設定為2，可以高效地在樹中插入、刪除、查詢資料
• 二叉查詢樹是一種特殊的二叉樹，相對較小的值儲存在左節點上，較大的值儲存在右節點上，這一特性使得查詢的效率很高

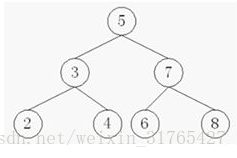
三、二叉查詢樹的實現

1、 二叉查詢樹由節點組成，或者說樹都是由節點組成，因此，我們要定義的第一個物件就是Node:

function Node(data){
    this.data = data;   //儲存鍵值
 

    this.left = left;   //指向左孩子的指標
    this.right = right; //指向右孩子的指標
    this.show = show;   //顯示儲存在節點中的資料
}
function show(){
    return this.data;
}

2、建立一個類，用來表示二叉查詢樹（BST）。類中只包含一個數據成員：root（一個用來表示二叉查詢樹的根節點的Node物件），初始化為null，從而建立一個空節點。

function BST (){
    this.root = null;
}

3、設計一個insert（）方法，用來向樹中加入新節點

• 建立一個Node物件，將資料傳入該物件中儲存
• 檢查BST是否有根節點，如果沒有，是一顆新樹，該節點為樹的根節點
• 如果該元素不是樹的根節點，則要遍歷BST，找到適合插入節點的位置，實現演算法：
  
  • 設根節點為當前節點
  • 如果待插入節點中儲存的資料小於當前節點，則設新的當前節點為原節點的左節點，否則，執行第四步
  • 如果當前節點為null，則插入節點，否則，繼續迴圈第二步
  • 如果待插入節點中儲存的資料大於當前節點，則設新的當前節點為原節點的右節點
  • 如果當前節點為null，則插入節點，否則，繼續迴圈第四步

function BST() {
    this.root = null;
    this
 
.insert = insert;
}

function insert(data) {
    var node = new Node(data,null,null);
    if(this.root == null) {
        this.root = node;
    } else {
        var currentNode = this.root;
        var parent;
        while(true) {
            parent = currentNode;
            if(data < currentNode.data) {
                currentNode = currentNode.left;
                if(currentNode == null) {
                    parent.left = node;
                    break;
                }
            } else {
                currentNode = currentNode.right;
                if(currentNode == null) {
                    parent.left = node;
                    break;
                }
            }
        }
    }
}

4、二叉查詢樹的遍歷

• 遍歷有三種方式
  （1）中序遍歷：按照節點上的鍵值，以升序訪問BST上的所有節點

function inOrder(node){
    if( node != null){
        inOrder(node.left);
        console.log(node.show()+' ');
        inOrder(node.right)
    }
}

（2） 先序遍歷：先訪問根節點，然後以同樣的方式訪問左子樹和右子樹

function preOrder(node){
    if(node != null){
        console.log(node.show());
        preOrder(node.left);
        preOrder(node.right)
    }
}

（3） 後序遍歷:先訪問葉子節點，從左子樹到右子樹再到根節點

function postOrder(node){
    if(node != null){
        postOrder(node.left);
        postOrder(node.right);
        console.log(node.show());
    }
}

• 測試程式

var nums = new BST();
nums.insert(23);
nums.insert(45);
nums.insert(16);
nums.insert(37);
nums.insert(3);
nums.insert(99);
nums.insert(22);

console.log("inOrder:")
inOrder(nums.root); //3 16  22  23  37  45  99
console.log("preOrder")
preOrder(nums.root); //23 16  3  22  45  37  99
console.log("postOrder")
postOrder(nums.root); //3  22  16  37  99  45  23

四、在二叉查詢樹上進行查詢
1、查詢最小值和最大值

• 查詢最小值：因為較小的值總是在左節點上，因此，在BST上要找到最小值，只需要遍歷左子樹，直到最後一個節點

function getMin(){
    var node = this.root;
    var parent;
    while(node != null){
        parent = node;
        node = node.left;
    }
    return parent.data;
}

• 查詢最大值：因為較大的值總是在右節點上，因此，在BST上要找到最大值，只需要遍歷右子樹，直到最後一個節點

function getMax(){
    var node = this.root;
    var parent;
    while(node != null){
        parent = node;
        node = node.right;
    }
    return parent.data;
}

• 使用上面的測試資料進行測試

console.log(nums.getMax());     //99
console.log(nums.getMin());     //3

2、查詢給定值

• 在BST上要查詢給定值，需要比較該值和當前節點上的值的大小。
• 通過比較，確定給定值不在當前節點時，該向左還是向右遍歷。

function find(data){
    var node = this.root;
    while(node != null){
        if(node.data == data){
            return node;
        }else if(node.data > data){
            node = node.left;
        }else{
            node = node.right;
        }
    }
    return null;
}

• 找到返回儲存該值的節點，沒有找到返回null
• 繼續使用上面的測試資料進行測試

console.log(nums.find("23"));
console.log(nums.find("100"));

五、在二叉查詢樹上刪除節點

• 判斷當前節點是否包含待刪除的資料，如果包含，刪除該節點
• 如果不包含，比較當前節點的資料和待刪除的資料，如果待刪除資料小於當前節點，則移至當前節點的左子節點繼續比較；如果待刪除資料大於當前節點，則移至當前節點的右子節點繼續比較；
• 刪除之後要保證仍然是個二叉樹
  
  • 如果待刪除節點是葉子節點，則將從父節點指向它的連結指向null
  • 如果待刪除節點只包含一個子節點，則從父節點指向它的連結指向它的子節點
  • 如果待刪除資料有兩個子節點
    
    • 查詢待刪除節點左子樹上的最大值
    • 查詢待刪除節點右子樹上的最小值
      eg - 給出如下二叉查詢樹：
      
      
      • 刪除節點3之後，你可以返回：
        
      • 或者：
        

function removeNode(node) {
    var root =  remove(this.root,node);
    return root;

}
function remove(node,data){
    if(node == null){
        return null;
    }
    if(data == node.data){
        //沒有子節點
        if(node.left == null && node.right == null){
            return null;
        }
        //沒有左子節點
        if(node.left == null){
            return node.right;
        }
        //沒有右子節點
        if(node.right == null){
            return node.left;
        }
        //有兩個子節點
        var tempNode = getMin(node.right);
        node.data = tempNode;
        node.right = remove(node.right,tempNode);
        return node;
    }else if(data < node.data){
        node.left = remove(node.left,data);
        return node;
    }else{
        node.right = remove(node.right,data);
        return node;
    }
}