導言：

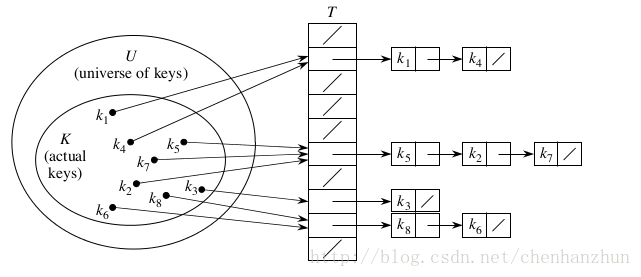
        陣列的特點是：定址容易，插入和刪除困難；而連結串列的特點是：定址困難，插入和刪除容易。那麼我們能不能綜合兩者的特性，做出一種定址容易，插入刪除也容易的資料結構？答案是肯定的，這就是我們要提起的雜湊表，雜湊表有多種不同的實現方法，我接下來解釋的是最常用的一種方法——拉鍊法，我們可以理解為“連結串列的陣列”，拉接法的思路是：如果多個關鍵字對映到了雜湊表的同一個位置處，則將這些關鍵字記錄在同一個線性連結串列中。結構如下圖所示：（注：以下是單鏈表實現，若為了方便刪除資料，也可以使用雙向連結串列實現）

直接定址表：

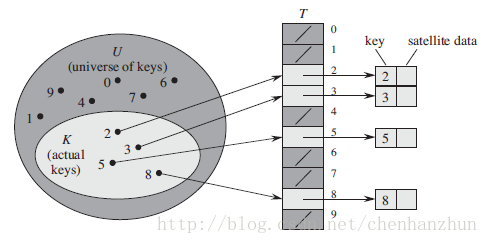
       當關鍵字的全域U比較小時，直接定址是一種簡單有效的技術。關鍵字大小直接與元素所在的位置序號相等，不會出現衝突的情況。其結構圖如下所示：

雜湊表：

       如果全域U很大時，直接定址表存在的很明顯的缺點。這時採用一種對映關係得到由雜湊值組成的雜湊表，使儲存空間利用率更高。但是，雜湊表存在的衝突情況，即不同的關鍵字在雜湊函式的對映下得到相同的雜湊值。為了解決這種衝突，可以採用一些有用的方法，例如：拉鍊法，開放定址等。雜湊表的確定主要是雜湊函式的選擇。

雜湊函式：

除法雜湊法

雜湊函式如下：

   式中表示在基數m中對關鍵字k取餘，其中m的取值最好為一個不太接近2的整數冪的素數。

乘法雜湊法

雜湊函式如下：

式中，m一般取2的某個次冪，k為關鍵字，A為某個引數一般取黃金分割值，kA(mod)1表示取kA的小數部分。

單鏈表實現的源程式：

#ifndef HASHTABLE_LINKLIST_H_INCLUDE
#define HASHTABLE_LINKLIST_H_INCLUDE

#define M 5

typedef int Elemtype;

typedef struct Node
{
	Elemtype data;
	struct Node *next;
}Node,*pNode;

typedef struct HashNode
{
	pNode head;
}HashNode,*HashTable;

//建立雜湊表
HashTable Creat_HashTable(int n);
//插入資料
void Insert_HashTable(HashTable HT,Elemtype data);
//查詢資料
pNode Search_HashTable(HashTable HT,Elemtype key);
//刪除資料
void Delete_HashTable(HashTable HT,Elemtype key);

#endif
 

/*****************************************
****該雜湊表是利用單鏈表解決衝突問題的****
*****************************************/

#include <stdio.h>
#include <stdlib.h>
#include "HashTable_LinkList.h"


//建立雜湊表
HashTable Creat_HashTable(int n)
{
	//分配雜湊表所需的地址空間
	HashTable HT = (HashTable)malloc(n*sizeof(HashNode));
	if (!HT)
	{
		printf("malloc the HashTable is failed.\n");
		exit(1);
	}
	//初始化空雜湊表
	int i;
	for (i = 0;i < n;i++)
	{
		HT[i].head = NULL;
	}
	return HT;
}
//插入資料
void Insert_HashTable(HashTable HT,Elemtype data)
{
	//查詢雜湊表是否存在要插入的資料
	//若存在則插入不成功，並退出
	if (Search_HashTable(HT,data))
	{
		printf("the data of %d you want to insert is exist.\n",data);
		exit(1);
	}
	else
	{
		pNode pNew = (pNode)malloc(sizeof(Node));
		if (!pNew)
		{
			printf("malloc the memory is failed.\n");
			exit(1);
		}
		//把資料插入到連結串列尾部
		pNew->data = data;
		pNew->next = NULL;
		//雜湊函式採用除法雜湊法
		int h = data%M;
		pNode pCur = HT[h].head;
		if (NULL == pCur)
		{
			HT[h].head = pNew;
		}
		else
		{
			while (pCur->next)
			{
				pCur = pCur->next;
			}
			pCur->next = pNew;
		}
		printf("Insert the data of %d is success.\n",data);
	}
	
}
//查詢資料
pNode Search_HashTable(HashTable HT,Elemtype key)
{
	if(!HT)
		return NULL;
	int h = key%M;
	pNode pCur = HT[h].head;
	while(pCur && pCur->data != key)
		pCur = pCur->next;
	return pCur;

}
//刪除資料
void Delete_HashTable(HashTable HT,Elemtype key)
{
	if (!Search_HashTable(HT,key))
	{
		printf("the data is not exist");
		exit(1);
	}
	else
	{
		int h = key%M;
		pNode pCur = HT[h].head;
		if(pCur->data == key)//該資料為第一個節點
			HT[h].head = pCur->next;
		else
		{
			pNode pre = pCur;//當前節點的前一個節點；
			while (pCur && pCur->data != key)
			{
				pre = pCur;
				pCur = pCur->next;
			}
			pre->next = pCur->next;
		}
		free(pCur);
		printf("delete the data of %d is success.\n",key);
	}
}

#include <stdio.h>
#include "HashTable_LinkList.h"

int main()
{
	int n_len = 10;
	int Array[]={1,5,8,10,15,17};
	//建立雜湊表並插入資料
	HashTable HT = Creat_HashTable(n_len);
	int i;
	for (i=0;i<6;i++)
	{
		Insert_HashTable(HT,Array[i]);
	}
	//查詢資料
	pNode p = Search_HashTable(HT,8);
	if (p)
	{
		printf("the data is exist.\n");
	} 
	else
	{
		printf("the data is not exist.\n");
	}
	//刪除資料
	Delete_HashTable(HT,15);
	p = Search_HashTable(HT,15);
	if (p)
	{
		printf("the data is exist.\n");
	} 
	else
	{
		printf("the data is not exist.\n");
	}
	return 0;
}

開放定址法：

   開放定址法是解決衝突的另一種辦法。

(1)線性探查：h(k,i)=(h'(k)+i) mod m，可能有“一次群集”問題，即隨著插入的元素越來越多，操作時間越來越慢。

(2)二次探查：h(k,i)=(h'(k)+ai+bi^2) mod m，可能有“二次群集”問題，即如果h(k1,0)=h(k2,0)，則探查序列就一致。

(3)二次雜湊：h(k,i)=(h1(k)+ih2(k)) mod m ，要求m和h2(k)互質，不然探查序列不能覆蓋到整個下標。演算法導論11.4-3證明了這點。

參考資料：