來源：http://study.163.com/course/courseMain.htm?courseId=1005232026

索引——

• 基本概念
• 連續變數的統計描述
• 分類變數的統計描述
• 正態分佈
• 二項分佈
• 引數估計與可信區間
• 假設檢驗

四、正態分佈

1、從樣本頻數分佈到概率分佈

     直方圖/頻率圖的性質：

（1）直條的面積實質上是頻率（或者百分比），即：

         面積 = 高度（頻率/組距） * 寬度（組距） = 頻率

（2）所有直條面積相加等於1

         樣本量越來越大時，頻率（面積）去向概率；

         組距越來越小時，直方圖的頂替所成點並且各個直方條的頂連結成一條曲線，該曲線就是概率密度分佈曲線；

         概率密度的概念和固體的密度基本類似。

（3）概率密度曲線下的面積就是相應的累計概率

（4）概率密度曲線就是大量重複隨機變異的規律

2、正態分佈和標準正態分佈

2.1 正態分佈，記為：X~N（μ，σ^2）

      正態分佈的倆個重要特徵：均數μ，標準差σ  

      μ是分佈曲線的峰位置（集中趨勢），又被稱為位置引數；

      σ（讀作：西格瑪）越大離散程度越大，σ越小離散程度越小（離散趨勢），又被稱為形狀引數；

      正態分佈是左右對稱的，具有對稱性。

2.2 標準正態分佈

2.2.1 統計學家計算出均數為0，標準差為1的正態分佈N（0,1）曲線下面幾分分佈規律：

          標準正態分佈N(0,1)與其他正態分佈N（μ，σ^2 ）的關係：

          若X~N（μ，σ^2） ，則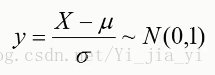       

2.2.2 標準正態分佈的曲線下面積分分佈規律

         只要將相應的指標轉換為服從標準正態分佈，就可以根據該面積分佈規律計算累計概率

3、正態分佈的應用

3.1 估計個體參考值；

3.2 整個經典統計學中更復雜方法的基石；

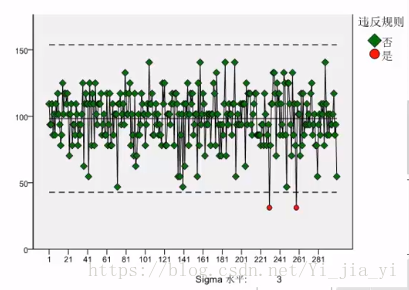
3.3 工業生產中的質量控制，如下圖

4、做正態分佈分析步驟

4.1 確定資料是否服從正態分佈：

• 若服從，直接採用正態分佈公式計算參考值範圍
• 若不服從，考慮是否可變換為正態分佈（對數轉換、平方根轉換），變換後採用正態分佈公式計算參考值範圍
• 無法變化，則使用百分位數法計算參考值範圍

    PS:    Q:不直接用百分位數法進行計算？

             A：百分位數法樣本容量太大不容易滿足條件

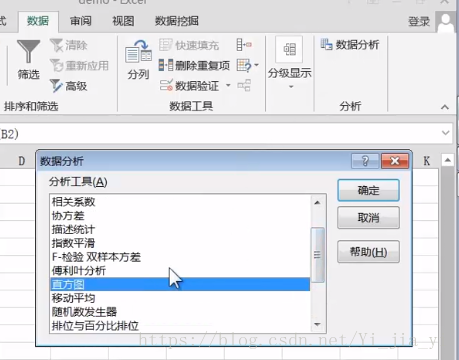
4.2 運用Excel 分析是否是正態分佈

   最簡單、直觀的方法是做出直方圖/頻數圖：

• 若直方圖剛好是左右對稱圖形則是正態分佈；
• 若不符合則可以考慮做變換（可用Excel函式SQRT()），再重新觀察分佈狀況。

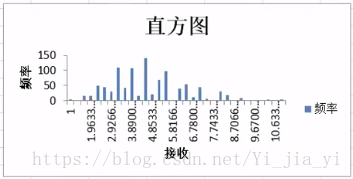
    如下圖，則是偏態分佈（大資料在小的一端）則不符合正態分佈，則做平方變換。

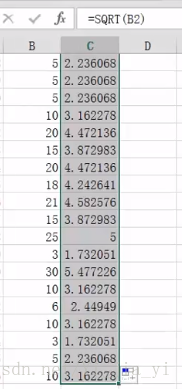
     （平方根轉換後）結果：轉換後並沒達到理想的正態分佈狀態；同理，這時可以考慮用對數轉換再檢視結果......