影象處理的一些相關知識(Related knowledge for IQA)
阿新 • • 發佈:2019-02-01
影象處理的一些相關知識
logistic transform
一般的logistic function
IQA演算法中使用的擴充套件的logistic function
- 公式1
f(x)=τ1−τ21+exp(x−τ3τ4)+τ2
τ1,τ2,τ3,τ4是使得預測值和DMOS、MOS值的MSE最小的參數 - 公式2
f(x)=β1(12−11+exp(β2(x−β3)))+β4∙x+β5
β1,β2,β3,β4,β5是使得預測值和DMOS、MOS值的MSE最小的參數
梯度下降、最小二乘法
資料
最小二乘法和梯度下降法的關係
相同
- 本質相同:兩種方法都是在給定已知資料(independent & dependent variables)的前提下對dependent variables算出出一個一般性的估值函式。然後對給定新資料的dependent variables進行估算。
- 目標相同:都是在已知資料的框架內,使得估算值與實際值的總平方差儘量更小(事實上未必一定要使用平方),估算值與實際值的總平方差的公式為:
不同
- 實現方法和結果不同:最小二乘法是直接對求導找出全域性最小,是
非迭代法。而梯度下降法是一種迭代法,先給定一個,然後向下降最快的方向調整,在若干次迭代之後找到區域性最小。梯度下降法的缺點是到最小點的時候收斂速度變慢,並且對初始點的選擇極為敏感,其改進大多是在這兩方面下功夫。
效能評估
皮爾森相關係數(Pearson correlation coefficient)
- X、Y的皮爾森相關係數的含義
- 當相關係數為0時,X和Y兩變數無關係。
- 當X的值增大(減小),Y值增大(減小),兩個變數為正相關,相關係數在0.00與1.00之間。
- 當X的值增大(減小),Y值減小(增大),兩個變數為負相關,相關係數在-1.00與0.00之間。
- 公式
- 試用範圍
- matlab 實現
- matlab函式 corr()
- 自寫函式
斯皮爾曼秩相關係數(SROOC)
肯德爾等級相關係數
可操縱金字塔變換(steerable pyramid transforms)
廣義高斯概率分佈
基本概念
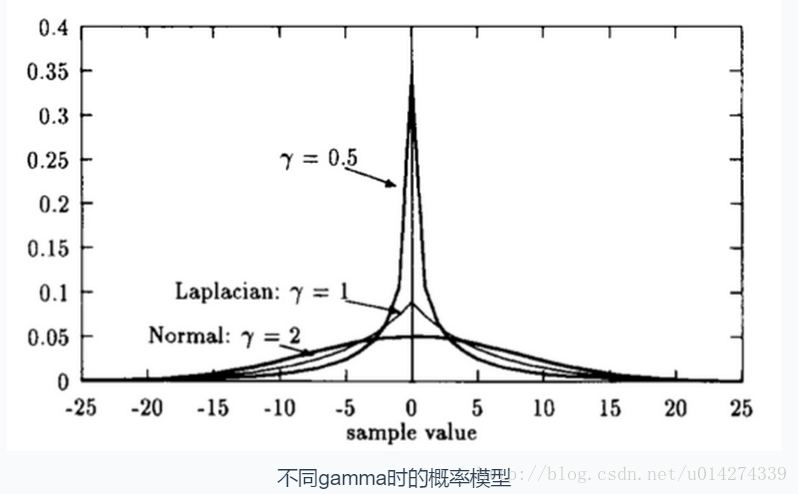
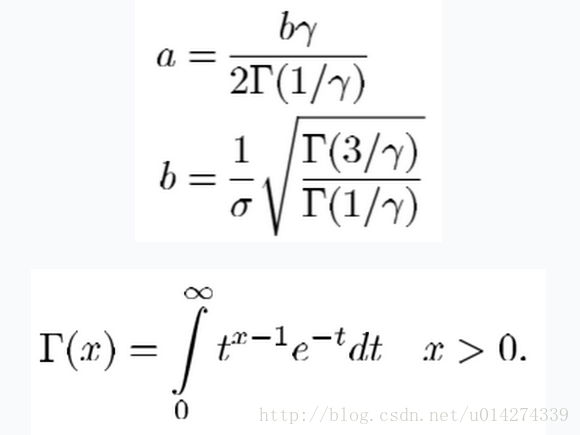
引數擬合與估計
樸素貝葉斯模型
文獻
箱狀圖
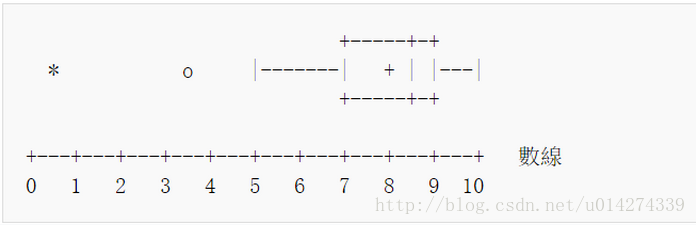
箱形圖於1977年由美國著名統計學家約翰·圖基(John Tukey)發明。它能顯示出一組資料的最大值、最小值、中位數、下四分位數及上四分位數。
舉例
- 這組資料顯示出:
- 最小值(minimum)=5
- 下四分位數(Q1)=7
- 中位數(Med)=8.5
- 上四分位數(Q3)=9
- 最大值(maximum )=10
- 平均值=8
- 最大值與最小值產生於這個區間。區間外的值被視為outlier顯示在圖上.
- mild outlier = 3.5
- extreme outlier = 0.5
離散餘弦變換 DCT
一維DCT變換
一維DCT變換時二維DCT變換的基礎,所以我們先來討論下一維DCT變換。一維DCT變換共有8種形式,其中最常用的是第二種形式,由於其運算簡單、適用範圍廣。我們在這裡只討論這種形式,其表示式如下:
其中,f(i)為原始的訊號,F(u)是DCT變換後的係數,N為原始訊號的點數,c(u)可以認為是一個補償係數,可以使DCT變換矩陣為正交矩陣。
二維DCT變換
二維DCT反變換
分塊DCT變換
在實際的影象處理中,DCT變換的複雜度其實是比較高的,所以通常的做法是,將影象進行分塊,然後在每一塊中對影象進行DCT變換和反變換,在合併分塊,從而提升變換的效率。具體的分塊過程中,隨著子塊的變大,演算法複雜度急速上升,但是採用較大的分塊會明顯減少影象分塊效應,所以,這裡面需要做一個折中,在通常使用時,大都採用的是8*8的分塊。