2. 程式人生 > >資料結構之堆的基本操作

資料結構之堆的基本操作

阿新 • • 發佈：2019-02-01

在實現堆的操作之前，先來明白什麼是堆？

  • 堆中某個節點的值總是不大於或不小於其父節點的值
  • 堆總是一棵完全二叉樹。

要說到完全二叉樹，直觀的判斷就是，層序遍歷一棵樹，如果樹的某個節點沒有右子樹或者是沒有子樹，那麼從這個節點後面的所有節點都不能夠有任何子樹。
這裡寫圖片描述

接下來我們說說堆。堆分為大堆跟小堆。大堆的意思就是每一個節點都是它這個節點樹的最大值。小堆同理是最小值。

基本操作與實現

基本操作

//heap.h

#pragma once

#include <stdio.h>
#include <stddef.h>

#define HEAPMAX 1000
 


typedef char HeapType;

typedef int(*Compare)(int a, int b);//函式指標，來確定將來的堆是最大堆還是最小堆

typedef struct Heap{
  HeapType data[HEAPMAX];
  size_t size;
  Compare cmp;
}Heap;

void HeapInit(Heap* heap, Compare cmp);//初始化堆

void HeapInsert(Heap* heap, HeapType to_insert);//在堆中插入

int HeapRoot(Heap* heap, HeapType* root);//取堆頂元素
 


void HeapErase(Heap* heap);//刪除堆頂元素

void HeapDestroy(Heap* heap);//銷燬堆

void HeapCreat(Heap* heap, HeapType array[], size_t size);//根據一個數組建立堆

void HeapSort(HeapType array[], size_t size);//堆排

實現

其實堆的操作都很簡單，但是最核心的兩個就是插入與刪除。這兩個我們單獨來說。

#include "heap.h"

#define HEAD printf("===================%s====================\n",__FUNCTION__);
 


void HeapPrintChar(Heap* heap)
{
  if(heap == NULL) {
    return;
  }
  size_t i = 0;
  for(; i < heap->size; ++i) {
    printf("%c ", heap->data[i]);
  }
  printf("\n");
}


int Greater(int a, int b)
{
  return a > b ? 1 : 0;
}

int Less(int a, int b)
{
  return a < b ? 1 : 0;
}

void HeapInit(Heap* heap, Compare cmp)//初始化堆
{
  if(heap == NULL) {
    return;
  }
  heap->size = 0;
  heap->cmp = cmp;
  return;
}

int HeapRoot(Heap* heap, HeapType* root)//取堆頂元素
{
  if(heap == NULL) {
    return 0;
  }
  if(heap->size == 0) {
    return 0;
  }
  *root = heap->data[0];
  return 1;
}

void HeapDestroy(Heap* heap)//銷燬堆
{
  if(heap == NULL) {
    return;
  }
  heap->size = 0;
  heap->cmp = NULL;
  return;
}

void HeapCreat(Heap* heap, HeapType array[], size_t size)//根據一個數組建立堆
{
  if(heap == NULL || array == NULL || size == 0) {
    return;
  }
  size_t i = 0;
  for(; i < size; ++i) {
    HeapInsert(heap, array[i]);
  }
  return;
}

插入

我們在實現堆的時，利用一個順序表來實現。由於是層序遍歷，且堆是完全二叉樹。所以順序表完全能夠處理好堆的基本操作。再者，定義一個函式指標，這個函式指標可以確定我們的堆是大堆還是小堆。接著就是插入了，由於要考慮到插入完畢後還是堆，那麼就要考慮到堆的性質，首先是完全二叉樹，接著每個節點都是它節點子樹的最大值或最小值。插入很簡單，我們只需要在順序表尾部插入即可。那如何保證堆的第二條性質呢？
這裡寫圖片描述
所以在插入的時候，要對插入的元素與它的父節點進行比較。而如何確定它的父節點呢？這很簡單，由於是層序遍歷在順序表內。那麼一個節點的父節點的下標就是它自己的下標減一除二。即parent = (child - 1)/2

//實現

void Swap(HeapType* a, HeapType* b)
{
  HeapType tmp = *a;
  *a = *b;
  *b = tmp;
}

void HeapInsert(Heap* heap, HeapType to_insert)//在堆中插入
{
  if(heap == NULL) {
    return;
  }
  if(heap->size >= HEAPMAX) {
    return;
  }
  heap->data[heap->size] = to_insert;
  ++heap->size;
  size_t child = heap->size - 1;
  size_t parent = (child - 1) / 2;//父節點

  while(child >= 0 && child < heap->size &&
        parent >= 0 && parent < heap->size) {
    if(heap->data[child] > heap->data[parent]){//判斷是否需要交換
      Swap(&heap->data[child], &heap->data[parent]);
      child = parent;//交換完畢後，要上浮，此時子節點變成之前的父節點，以此類推
      parent = (child - 1) / 2;
    } else {
      break;
    }
  }
  return;
}

刪除

在實現完插入之後，接下來就是刪除。同樣，刪除也得滿足刪除後的樹仍舊是一個堆。且滿足堆的基本條件。這裡，我們的思路採用的是刪除堆頂。具體如下：
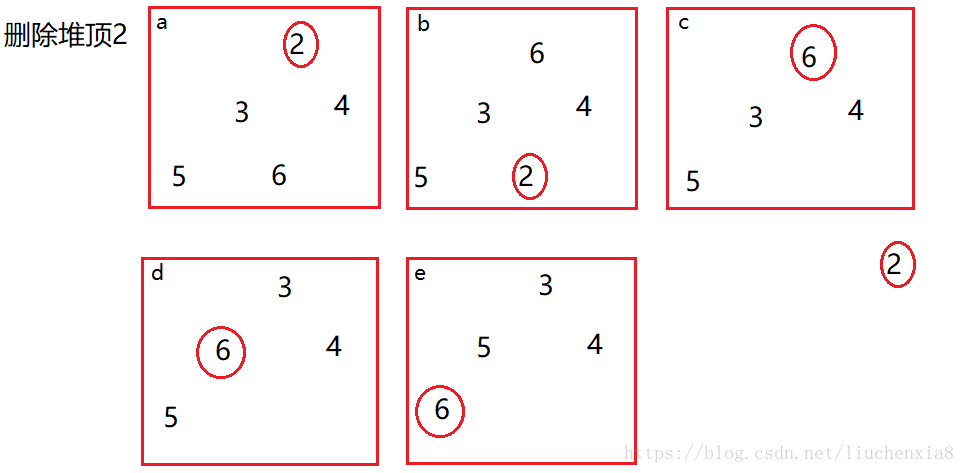
這裡寫圖片描述
這裡，我們在刪除之前，先將堆頂元素與最後一個元素交換，然後刪除最後一個元素，也就是結構體內的size減一。刪除完畢後，開始調整。調整的過程就是下沉。此時堆頂是6，先將節點元素與其左右子樹分別比較。將左右子樹中較小的與節點交換。如果沒有右子樹，那麼直接與左子樹交換。一次交換完畢後，此時新節點等於交換的子樹。以此類推。這就是下沉。

//實現

void HeapErase(Heap* heap)//刪除堆頂元素
{
  if(heap == NULL) {
    return;
  }
  if(heap->size == 0) {
    return;
  }
  Swap(&heap->data[heap->size - 1], &heap->data[0]);
  --heap->size;
  size_t parent = 0;
  size_t child = 2*parent + 1;//交換並刪除

  while(child >= 0 && child< heap->size &&
        parent >= 0 && parent < heap->size) {
    if((child + 1) < heap->size){//判斷是否有右子樹，並且取出其中較小的
      if(!heap->cmp(heap->data[child], heap->data[child+1])) {
        child = child + 1;
      }
    }
    if(heap->data[child] > heap->data[parent]) {//判斷是否需要下沉
      Swap(&heap->data[child], &heap->data[parent]);
      parent = child;
      child = 2*parent + 1;
    } else {
      break;
    }
  }
  printf("\n");
  return;
}

堆排

在實現完堆的基本操作以後，我們可以考慮一下堆排序的實現。我們其實可以發現，在刪除堆內元素的時候每次刪除的都是最大的一個。並且最大或最小的一個都沉底了。
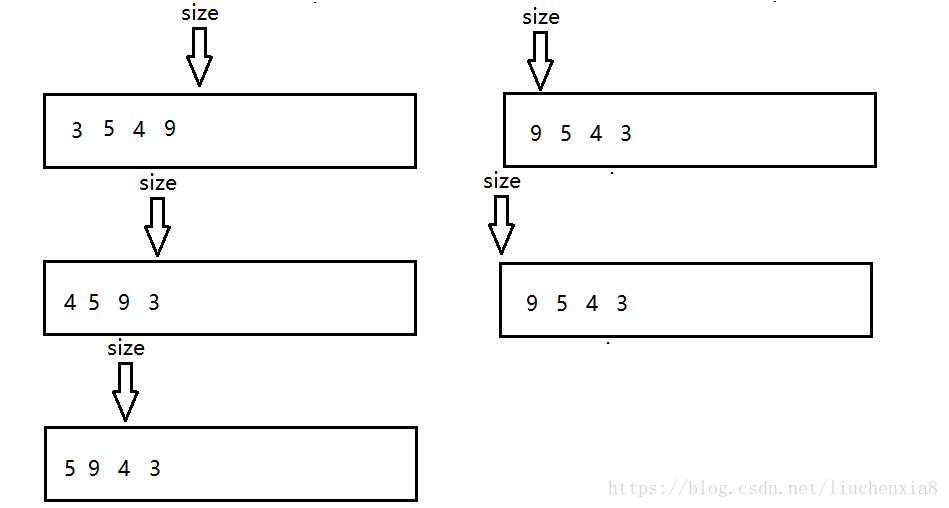
這裡寫圖片描述
我們發現，每次刪除一次，後面的元素都是一個有序的。而刪除到最後，整個順序表就是一個有序的順序表。如果這時候將size放到最後，那麼此時恰好就是一個有序的陣列。

//實現

void HeapSort(HeapType array[], size_t size)//堆排
{
  if(array == NULL || size == 0) {
    return;
  }
  Heap heap;
  HeapInit(&heap, Greater);
  HeapCreat(&heap, array, size);//先將陣列插入堆中
  size_t i = 0;
  for(; i < size; ++i) {
    HeapErase(&heap);//刪除堆內所有元素
  }
  heap.size = size;
  i = 0;
  for(; i < size; ++i) {
    array[i] = heap.data[i];//把堆內元素複製到陣列中，完成排序
  }
  return;
}

測試程式碼如下

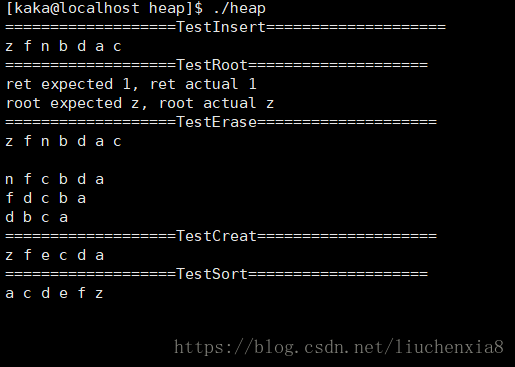
void TestInsert()
{
  HEAD;
  Heap heap;
  HeapInit(&heap, Greater);
  HeapInsert(&heap, 'b');
  HeapInsert(&heap, 'z');
  HeapInsert(&heap, 'a');
  HeapInsert(&heap, 'f');
  HeapInsert(&heap, 'd');
  HeapInsert(&heap, 'c');
  HeapInsert(&heap, 'n');
  HeapPrintChar(&heap);
}

void TestRoot()
{
  HEAD;
  Heap heap;
  HeapInit(&heap, Greater);
  HeapInsert(&heap, 'b');
  HeapInsert(&heap, 'z');
  HeapInsert(&heap, 'a');
  HeapInsert(&heap, 'f');
  HeapInsert(&heap, 'd');
  HeapInsert(&heap, 'c');
  HeapInsert(&heap, 'n');
  HeapType root;
  int ret = HeapRoot(&heap, &root);
  printf("ret expected 1, ret actual %d\n",ret);
  printf("root expected z, root actual %c\n",root);
}

void TestErase()
{
  HEAD;
  Heap heap;
  HeapInit(&heap, Greater);
  HeapInsert(&heap, 'b');
  HeapInsert(&heap, 'z');
  HeapInsert(&heap, 'a');
  HeapInsert(&heap, 'f');
  HeapInsert(&heap, 'd');
  HeapInsert(&heap, 'c');
  HeapInsert(&heap, 'n');
  HeapPrintChar(&heap);
  printf("\n");
  HeapErase(&heap);
  HeapPrintChar(&heap);
  HeapErase(&heap);
  HeapPrintChar(&heap);
  HeapErase(&heap);
  HeapPrintChar(&heap);
}

void TestSort()
{
  HEAD;
  HeapType array[] = {'c', 'd', 'a', 'f', 'z', 'e'};
  size_t size = sizeof(array)/sizeof(array[0]);
  HeapSort(array, size);
  size_t i = 0;
  for(; i < size; ++i) {
    printf("%c ", array[i]);
  }
  printf("\n");
}

void TestCreat()
{
  HEAD;
  Heap heap;
  HeapInit(&heap, Greater);
  HeapType array[] = {'c', 'd', 'a', 'f', 'z', 'e'};
  size_t size = sizeof(array)/sizeof(array[0]);
  HeapCreat(&heap, array, size);
  HeapPrintChar(&heap);
}

int main()
{
  TestInsert();
  TestRoot();
  TestErase();
  TestCreat();
  TestSort();



  printf("\n");
  printf("\n");
  printf("\n");
  printf("\n");
  printf("\n");


  return 0;
}

這裡寫圖片描述

歡迎大家共同討論，如有錯誤及時聯絡作者指出，並改正。謝謝大家！

相關推薦

資料結構之堆的基本操作

在實現堆的操作之前，先來明白什麼是堆？ 堆中某個節點的值總是不大於或不小於其父節點的值 堆總是一棵完全二叉樹。 要說到完全二叉樹，直觀的判斷就是，層序遍歷一棵樹，如果樹的某個節點沒有右子樹或者是沒有子樹，那麼從這個節點後面的所有節點都不能夠有任何子樹。

資料結構之連結串列操作（c++實現）

1、單向連結串列（頭結點不含資料，不佔長度），C++實現： #include <iostream> #include <stack> using namespace std; /*****定義節點****/ typedef struct node{ int va

資料結構棧的基本操作

#include<iostream> #define MAXSIZE 100 #define OVERFLOW -1 #define OK 1 #define ERROR 0 using namespace std; typedef int SElemType

資料結構之樹的操作

話不多少 q：690217293  歡迎交流 //_____________________________demo.cpp #include <cstdio> #include "Tree.h" #include <iostream> using

案例3.2：括號匹配的檢驗（c++實現/資料結構/棧的基本操作）

#include<iostream> #define MaxSize 100 #define OK 1 #define ERROR 0 using namespace std; typedef char ElemType; typedef int Status

資料結構串的基本操作--賦值，列印，連線

//#include<iostream> #include<stdio.h> #include<stdlib.h> #include<string> #include<string.h> using namespac

python資料結構之序列及其操作

序列       在Python中最基本的資料結構是序列（sequence）。序列中的每個元素被分配一個序號----即元素的位置，也稱索引。索引從0開始，0,1,2,3，...。也可以從最後一個數開始，標記為-1，依次為-1，-2，-3.... 列表與元組的區別

資料結構 圖的基本操作實現

實驗題目： 圖的基本操作實現        實驗環境：   Visual C++ 6.0                   　 實驗目的：掌握圖的鄰接矩陣和鄰接表兩個儲存結構及表示。           掌握圖的DFS和BFS兩種遍歷演算法。           理解並

資料結構-鏈佇列基本操作

都是些基本操作，有興趣的可以看看。 1 #include<stdio.h> 2 #include<stdlib.h> 3 typedef struct QNode { 4 int data; 5 struct QNode *next; 6 }QNod

資料結構之堆（Heap）的實現

  堆資料結構是一種陣列物件，它可以被視為一棵完全二叉樹結構，所以堆也叫做二叉堆。二叉堆滿足二個特性：  1．父結點的鍵值總是大於或等於（小於或等於）任何一個子節點的鍵值。  2．每個結點的左子樹和右子樹都是一個二叉堆（都是最大堆或最小堆）。  當父結點的鍵值總是大於或等於任

資料結構之堆排序C語言實現

堆排序： 時間複雜度：O(nlogn) 穩定性：不穩定 實現原理：將待排序的序列構造成一個大頂堆(或小頂堆) 整個序列的最大值就是堆頂的根節點，將它移走 (就是將其與對陣列的末尾元素交換，此時末尾元素就是最大值)。然後將剩餘的n-1個序列重新 構成

演算法與資料結構-棧的基本操作C語言實現

序言 複習棧的基本操作及其C語言實現，主要以鏈式棧為例。 本文將介紹棧的以下基本操作： 棧的建立（順序棧和鏈式棧） 棧的初始化 棧遍歷 棧清空/銷燬 判斷棧是否為空 求棧的長度 返回並刪除棧頂元素 1. 棧建立 - 順序棧和鏈式棧 //順序棧的

資料結構-串-StringBuffer基本操作(JAVA)

StringBuffer和String類的區別是StringBuffer中的陣列有緩衝，所以不需要每次進行插入操作都重新申請陣列，提高了空間利用效率。這裡實現了一些StringBuffer的基本操作(幾個構造方法，查入和刪除操作)。 public class MyStrin

演算法與資料結構之堆的相關知識，簡單易懂。

十、 二叉堆之Java的實現 1) 概要 前面分別通過C和C++實現了二叉堆，本章給出二叉堆的Java版本。還是那句話，它們的原理一樣，擇其一瞭解即可。 目錄 1. 二叉堆的介紹 2. 二叉堆的圖文解析 3. 二叉堆的Java實現(完整原始碼) 4. 二叉堆的Java測試程式

資料結構之連結串列操作

之前看資料結構時，以為連結串列操作很容易，真正寫程式碼時才發現被打臉了。。。經歷了各種錯誤後，現在總結一下走過的彎路。 這裡主要說下連結串列的增加刪除節點操作。 typedef struct l

資料結構之堆的簡單實現

堆的主要介面包括，堆的初始化，堆的銷燬，堆的插入，堆的刪除，獲取堆頂的資料，判斷堆是否為空，求堆的大小，以及堆的氣泡排序。在這裡還有堆的簡單的資料結構的實現。因為堆是動態增長的，所以實現堆的資料結構裡包含一個存放資料的堆的陣列data，堆的大小sz，以及堆的容量capacit

資料結構——棧的基本操作（二進位制轉十進位制例項—c語言程式碼）

棧棧是一種重要的線性結構。棧必須通過線性表或者連結串列來實現，順序表點選開啟連結和連結串列點選開啟連結既可以向之前介紹的那樣獨立存在，同時它們也是一些特殊的資料結構（棧，佇列）的實現基礎。定義：棧是一個先進後出的線性表，只要求在表尾進行插入和刪除等操作，這是棧相對於連結串列和

資料結構—順序表基本操作（c語言程式碼）

順序表計算機內部儲存一張線性表是用一組連續地址記憶體單元，這種儲存結構即為順序儲存結構，這種結構下的線性表叫順序表。順序表有兩種定義方法：                                    1.靜態定義                           

演算法與資料結構-佇列的基本操作C語言實現

序言 佇列有順序佇列和鏈式佇列，順序佇列通過陣列方式來實現，鏈式佇列通過連結串列方式來實現。 陣列方式實現便於資料訪問（大小和空間確定），連結串列方式實現便於資料操作（插入和刪除靈活）。 這裡介紹

資料結構：字串(堆)——基本操作

資料結構的重要行不言而喻，簡單介紹我在這部分遇到的一些問題，希望對大家有少許幫助。 首先實現的多個操作： 程式碼： #include<stdio.h> #include<stdlib.h> #include<string.h> #defi