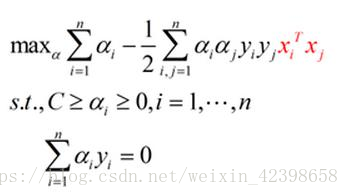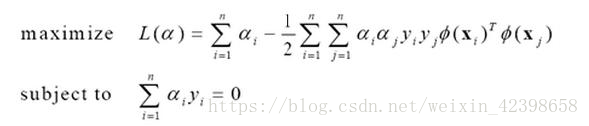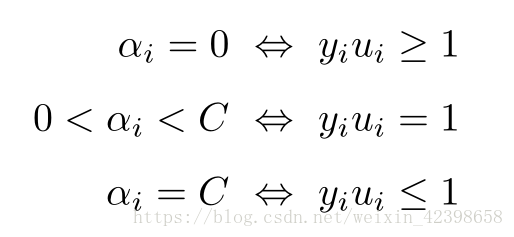機器學習--支援向量機(五)核函式詳解
前面我們曾經引入二維資料的非線性的情況,但是那種非線性(並不是真正意義上的非線性)是通過鬆弛因子進行優化的,如果資料比之前還複雜怎麼辦呢?
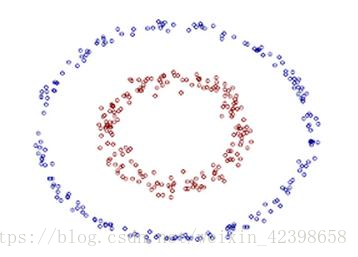
複雜到即使你怎麼調節C你都無法進行分類,這個時候怎麼辦?如下例子:
這個無論你怎麼調節引數都無法在二維平面內進行線性分離了,但是我們也可以觀察到,分離的辦法就是在兩個資料中間畫一個圓就可分了,但是這非線性了,我們就想通過線性分離怎麼辦呢?這個時候可以通過對映到高維空間即可,下面詳解如何對映,我覺的這裡的理解很重要,直接影響後面的核函式的理解,所以大家務必好好理解這個簡單的例子,好廢話不多說開始繼續,怎麼把這個線性不可分變為線性可分,然後在通過前面計算線性可分的方法進而求出分離超平面:
上圖的資料在二維平面中就是兩個圓,使用線性分離不可能實現,那麼我們可以對映,什麼對映呢?即我們把二維資料對映到更高維度中,我們的資料是二維的,但是我們可以對映到三維去看看資料,
如左圖為二維的資料,黑色圓圈為一種資料,紅色為另外一種資料,很明顯紅色的半徑要大於黑色的半徑,且此時在二維無法線性可分,那麼我們就想到對映到更高維度進行分離,因此我們把二維資料對映到三維,對映規則是,所謂三維其實很簡單就是在二維的基礎上增加一維,這一維的怎麼新增就是對映規則,在這裡我們的對映規則為
,即第三維其實就是z軸,且這一維的值就是
即圓的半徑r,那麼就可以畫出三維的資料圖形了,簡單來看,就是把二維資料沿著z軸進行平移,平移的大小和對映有關,這裡我們對映規則是圓的半徑,因為兩圓的的半徑不同,因此z值不同,也就是表現的高度不同,如上右圖,我們可以清楚的看到,紅色代表的資料要比黑色代表的資料高,同時二者在三維也就分離開了,此時使用一個平面就可以分離這兩種資料,如上圖鉛筆畫的分離平面,因此在這裡,我們就可以使用前面的解決思路求出這個平面即可,同時我們可以以此類推,如果資料更復雜,維度更高,那麼我們就可以對映到更高的維度,直到,他們可以通過線性分離實現,此時的線性就是超平面了,這個超平面就可以通過支援向量進行確定,即又回到前面的求線性分離超平面問題了,通過引入拉格朗日因子,鬆弛因子、在轉換為對偶問題,最後通過smo演算法即可求出超平面,當然這些是在知道如何對映的問題之上,所以,如果我們遇到了線性不可分問題就可以令其對映到更高維度就可以解決了。如下在二維的資料最後對偶問題是這樣的:
現在呢把資料對映到更高維度,而這個對映函式使用,代入上式得到:
到這裡我們呢基本上就可以解決各種非線性問題了,無論資料多複雜都沒問題,因為可以通過n維對映進行分離,理論上是可以解決各種複雜的非線性問題,這就是支援向量機的牛叉之處,但是呢,這一切實現的前提是找到合適的對映函式,同時還有一個問題不可忽視那就是計算量,在這裡先說一下計算量問題:
首先呢,我們知道在對映之前呢資料只需求內積就好即,假如是n維資料,那麼時間複雜度為O(n),如果對映到
維,內積就變為
那麼時間複雜度就是
維,計算量陡然增加,隨著對映維度越高,那麼計算量會陡然增加,這就是維度災難了,同時呢?對映函式怎麼找呢?如何找?
所以支援向量雖然從理論上可以解決任意的非線性分類問題,但是代價卻是很大的,一是計算量、二是對映函式如何尋找問題
在很長時間裡人們都在想辦法解決這兩個問題,終於找到了一個方法,那就是核函式,他的主要解決思路是本來我需要找到對映函式,把資料對映到高維在通過求解超平面進行分離,在求解超平面時會遇到維度災難問題,但是呢我不需要這樣做了,我能找到一種核函式把這個過程(把資料對映到高維在通過求解超平面進行分離)的計算結果直接通過核函式來代替,即資料對映到高維計算的結果,我可以通過低維的核函式進行計算出這個結果,這樣就避免去找這個對映函式同時避免了維度災難,這就是核函式的牛叉之處,也因此核函式的出現,支援向量機才得到廣泛的使用,這裡只是感性讓大家認識一下核函式,下面通過數學方式進行詳解什麼是核函式。
核函式形式化定義,如果原始特徵內積是,對映後為
,那麼定義核函式(Kernel)為
從這個定義的式子我們可以看出,按照正常的處理方式是通過找到對映函式,然後在高維進行內積,現在呢,我可以通過核函式直接計算出這個結果,下面舉個例子進行說明:
假設x和z都是n維的
![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png)
展開後
![clip_image030[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034348235.png)
這時候我們發現核函式計算內積的平方,時間複雜度還是O(n)而不是,因此核函式可以降低計算量
好到這裡我們就解決了計算量和對映問題,那麼我們我們如何去分類一個新來的資料呢?我們知道線上性可分的問題中,我們通過smo演算法進行求解w、b,然後把通過 進行分類,然而我們對映後需要通過
進行求解嗎?
理論上說應該這樣,但是我們通過核函式計算就沒有去找對映函式呀,這怎麼辦呢?其實根本用不到對映函式,如下圖:
![clip_image055[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034444670.png)
其中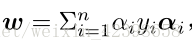
現在我們在細看這個式子其中:
我們發現最後我們預測資料x時只需和每一個訓練資料進行內積 就可以了,然而高維進行內積計算量大且不易找到對映函式,因此通過核函式解決,根據前面我們引入拉格朗日乘子可知,只要訓練資料點
分類正確,此時
=0,大家可以看到一旦
=0,此時的在預測中就不會參與運算,只有在分界線上的資料點才會參與運算,也就是說在預測的時候真正參與運算的只是那些支援向量,以及那些通過鬆弛變數引入的資料點,因此計算量會很少,下面給出圖示:
此圖是沒有加入鬆弛條件的支援向量,圓圈你的就是支援向量,預測的時候也就是新資料和這些支援向量進行內積就可以了。
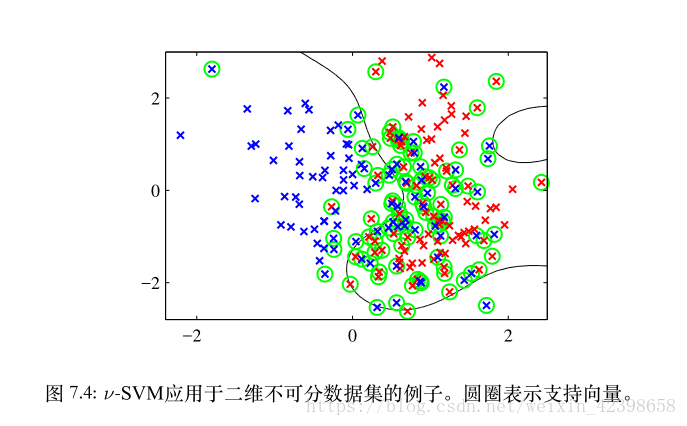
下圖是加入鬆弛變數,我們發現加入鬆弛變數的支援向量變多了,說明了鬆弛變數的的有效性
好,到這裡我們已經講解了如何尋找對映函式和解決維度災難問題,現在的問題是到底什麼是核函式?為什麼核函式具有這樣的特性?這個核函式又是怎麼確定的?是不是核函式是不是任意的還是有所約束呢?
核函式算式一種近似,和數學中的泰勒級數以及傅立葉變換性質差不多,就是一種近似,然後這種近似並不是無條件的的,他需要滿足一定的條件,這個條件是Mercer定理,下面開始從核函式的有效性進行講解。
核函式有效性判定:
問題:給定一個函式K,我們能否使用K來替代計算 ,也就說,是否能夠找出一個
,使得對於所有的x和z,都有
![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png) ?
?
比如給出了![clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182034334920.png) ,是否能夠認為K是一個有效的核函式。
,是否能夠認為K是一個有效的核函式。
下面來解決這個問題,給定m個訓練樣本![]() ,每一個
,每一個![]() 對應一個特徵向量。那麼,我們可以將任意兩個
對應一個特徵向量。那麼,我們可以將任意兩個![]() 和
和![]() 帶入K中,計算得到
帶入K中,計算得到![]() 。I可以從1到m,j可以從1到m,這樣可以計算出m*m的核函式矩陣(Kernel Matrix)。為了方便,我們將核函式矩陣和
。I可以從1到m,j可以從1到m,這樣可以計算出m*m的核函式矩陣(Kernel Matrix)。為了方便,我們將核函式矩陣和![]() 都使用K來表示。
都使用K來表示。
如果假設K是有效地核函式,那麼根據核函式定義
可見,矩陣K應該是個對稱陣。讓我們得出一個更強的結論,首先使用符號![]() 來表示對映函式
來表示對映函式![]() 的第k維屬性值。那麼對於任意向量z,得
的第k維屬性值。那麼對於任意向量z,得
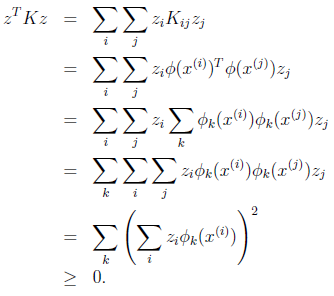
最後一步和前面計算![]() 時類似。從這個公式我們可以看出,如果K是個有效的核函式(即
時類似。從這個公式我們可以看出,如果K是個有效的核函式(即![]() 和
和![]() 等價),那麼,在訓練集上得到的核函式矩陣K應該是半正定的(
等價),那麼,在訓練集上得到的核函式矩陣K應該是半正定的(![]() )
)
這樣我們得到一個核函式的必要條件:
K是有效的核函式 ==> 核函式矩陣K是對稱半正定的。
可幸的是,這個條件也是充分的,由Mercer定理來表達。
Mercer定理:
如果函式K是![]() 上的對映(也就是從兩個n維向量對映到實數域)。那麼如果K是一個有效核函式(也稱為Mercer核函式),那麼當且僅當對於訓練樣例
上的對映(也就是從兩個n維向量對映到實數域)。那麼如果K是一個有效核函式(也稱為Mercer核函式),那麼當且僅當對於訓練樣例![]() ,其相應的核函式矩陣是對稱半正定的。
,其相應的核函式矩陣是對稱半正定的。
Mercer定理表明為了證明K是有效的核函式,那麼我們不用去尋找![]() ,而只需要在訓練集上求出各個
,而只需要在訓練集上求出各個![]() ,然後判斷矩陣K是否是半正定(使用左上角主子式大於等於零等方法)即可。
,然後判斷矩陣K是否是半正定(使用左上角主子式大於等於零等方法)即可。
核函式不僅僅用在SVM上,但凡在一個模型後演算法中出現了,我們都可以常使用
去替換,這可能能夠很好地改善我們的演算法。
到這裡基本核函式就講解完了,下一節將講解幾個重要的核函式,即
注:本篇的 核函式有效性判定來源這篇部落格,本人感覺這裡作者寫的很詳細了,就沒再自己編寫,在這裡特此說明。