這是之前手遊專案中琢磨出來的一個簡單易行, 同時感覺比較高效的一個尋路演算法.  當然有一個前提, 是基於格子的尋路, 你的格子可以是正方形, 六邊形等. 總之, 從一個格子移動到旁邊任何一個格子的代價是相等的, 也就是步數都是一, 這個演算法可能也適應於其它場景, 當然我對尋路演算法也沒什麼研究, 僅僅是解決了我所遇到的問題.

這是一個最短路徑尋路演算法.

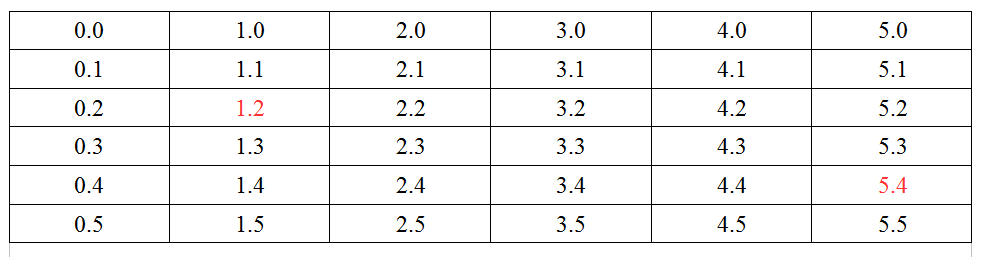
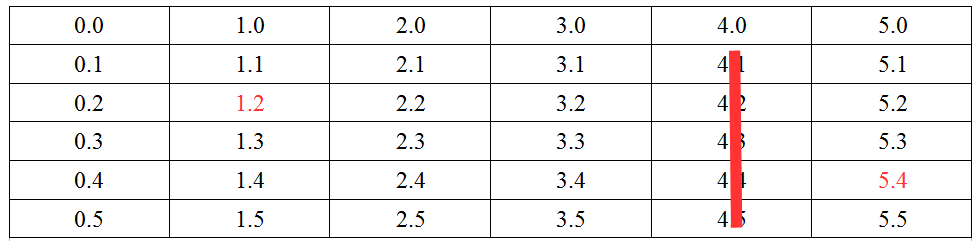
地圖如下, 6 * 6,  當時專案中實際的地圖尺寸為5 * 14, 沒有關係. 原理是一樣的. 

假設我們要從1.2(x = 1, y = 2)移動到5.4, 圖中的紅色部分.

如果地圖上沒有任何障礙, 那麼其中一條(有多條)最短路徑可能是 1.2-->2.2-->3.3-->4.4-->5.4, 一共是4步. 演算法的實現步聚如下:

1. 開放列表(存放等待掃描其周圍的格子) .

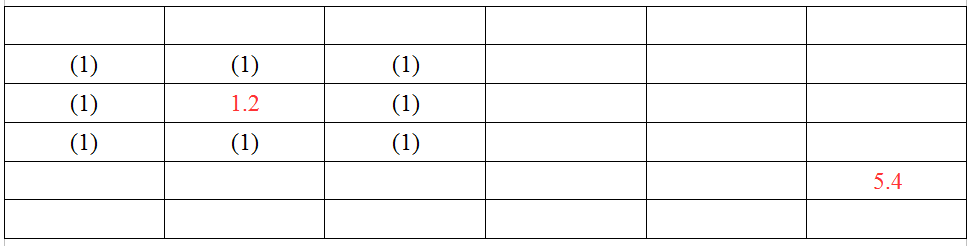
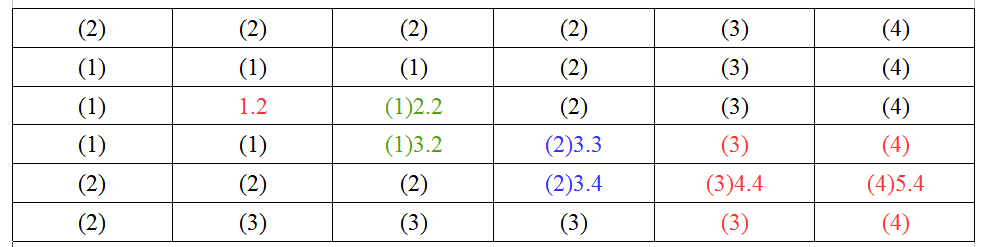
將1.2加入到開放列表. 掃描它的周圍, 理論上, 如果你是四邊形的格子, 那麼任何一個格子的周圍都有8個格子(不考慮邊界), 掃描完後, 記下這8個格子到1.2這個座標的距離, 都是一步, 所以下面這個圖中標記的全是1, 這是第一輪掃描.

2. 將1.2從開放列表中移除(它已經掃描過了), 並將剛才掃描的8個格子加入到開放列表.

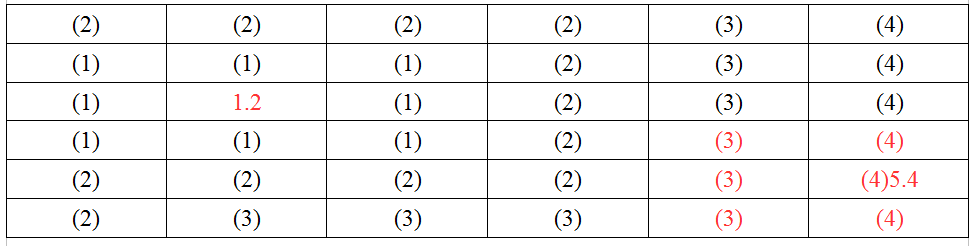
3. 掃描這8個格子的周圍, 將它們周圍未掃描過(已掃描過的不要參與)的格子標記距離為2, 這是第二輪掃描, 結果如下.

4. 依次類推, 掃描完剩餘的格子, 這裡的規律是, 第一輪掃描的格子的距離離出發點一定是1, 第二輪掃描的離出發點一定是2.  第三輪一定是3. 直到掃完所有的格子, 最終的結果如下:

5. 好了, 如何得到最短路徑呢? 

關閉列表(被選擇到最終路徑中的格子).

我們將5.4加入到關閉列表. 並掃描它周圍每一個格子所標記的步數(從起點1.2過來的步數),  會得到六個格子, 有兩個格子(5.3, 5.5)到1.2有四步, 另外有三個格子到1.2只有三步, 換句話說, 在這裡我們至少有3條最短的路可以回到1.2, 選擇任何一條都可以, 如下圖.

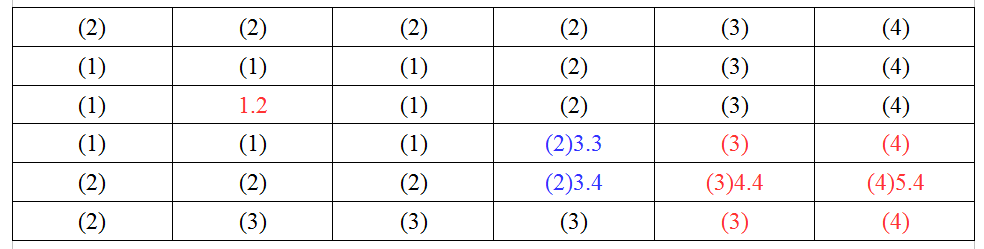
6. 隨便(如果你想角色移動的比較合符自然規律的話, 不能隨便選)選一個, 我們就選4.4, 也就是5.4正左邊的這個格子, 將它加入到關閉列表, 然後再掃描4.4周圍的格子, 同樣找出到1.2需要最少步數的格子, 這裡有兩個(3.4, 3.3), 如下圖.

7. 還是隨便選一個, 3.3, 繼續掃描,  得到2.2和3.3兩個距離1.2的步數都為1的格子, 如下:

8. 再隨便選一個2.2, 再往下掃, 就能碰到1.2了, 接著就不用再掃了, 這個時候, 關閉列表中已經存在一條最短路徑了. 是: 5.4-->4.4->>3.3-->2.2-->1.2

9. 有人要問, 為什麼是從終點5.4向起點1.2反向掃描呢? ^:^

10. 有障礙的情況下, 如何處理? 如下圖中, 4.1, 4.2,4.3, 4.4, 4.5都無法通過.

 其實還是按照之前的掃描方式就可以了, 只是當碰到障礙時不用標記, 最終掃描的結果如下, 一樣可以得到最短路徑.

11. 優化, 這個演算法存在一些優化的可能, 例如.

a). 如果1.2至5.4方向的前一排, 即2.0 ~ 2.5全部無障礙時, 我們就可不必掃描1.2身後所有格子, 因為這時不必繞路. 如果1.2在地圖中間, 那將有一半的格子不用參與計算.

b). 某些條件下是否可以掃描到5.4之時, 對身後的格子不再掃描? 這樣, 如果5.4在地圖中間, 那麼也將有一半的格子不用參與計算.

 請尋路演算法高手不吝賜教, 另外, 上面有幾張圖有個小錯誤: 0.5這個格子應該標註為(3), 而不是(2).