增強學習(二)——策略迭代與值迭代
在上一篇文章中,我主要介紹了馬爾可夫決策過程(MDP)。在瞭解了增強學習的基本思想後,我們便可以繼續討論“最優策略”的求解方法:
我們之前已經說到了MDP可以表示成一個元組(X, A, Psa, R),我們對最優策略的求解方法自然也就與這個元組密切相關:如果該過程的四元組均為已知,我們稱這樣的模型為“模型已知”,對這種已知所有環境因素的學習稱為“有模型學習”(model-basedlearning);與之對應的就是“無模型學習”,環境因素機器無法得知的,主要是指狀態轉移概率Pxa。
本篇部落格對“有模型學習”的兩種方法進行介紹,分別是策略迭代和值迭代。在此之前,我們需要明確增強學習的兩大步驟,策略評估與策略改進:
策略評估:
在上一篇部落格中,我們已經對“狀態值函式”和“狀態動作值函式”進行了簡單介紹,但在之前的考慮中,我們是認為策略已知,故在貝爾曼方程中沒有考慮策略π的取值與改進問題。我們在此以“狀態值函式”和“狀態動作值函式”的T步累積獎賞為例重新進行完整的推導:
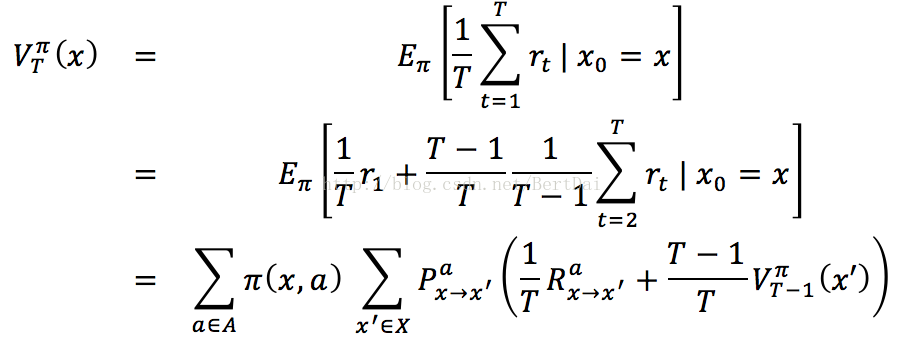
關於下標,Rax->x’表示的是在x狀態下采取a動作,轉移到x’狀態後得到的回報,其他的類比即可。同理可以得到關於“狀態動作值函式”Q的公式:

這樣的遞迴式才是對於完整的MDP四元組的貝爾曼等式。也就是說,我們通過這兩個公式,就可以通過逐步遞迴的方式,在程式設計上實現對策略π的評估。虛擬碼如下:

策略改進:
由於我們已經知道了怎樣對策略進行評估,那麼,我們可以產生一個很直接的求解最優策略的方法:從一個初始化的策略出發,先進行策略評估,然後改進策略,評估改進的策略,再進一步改進策略……不斷迭代更新,直達策略收斂,這種做法被稱為“策略迭代”,虛擬碼如下:

其中,Q的計算是根據公式(2)來進行的。
此外,我們不難理解,當Qπ(x,π’(x))>=Vπ(x)時,我們可以認為在x的狀態下,π’策略相比原來的策略更好。再結合上一篇博文中的最優貝爾曼方程,我們可以將策略的改進視為值函式的改善,以此得出“值迭代”方法,虛擬碼如下:

但是,這兩種方法的缺點顯而易見:必須知道狀態轉移概率才能進行最優策略的計算。這在我們真實的使用場景中幾乎不可能實現,所以,我們將在下一篇中介紹適用性更強的“無模型學習”。
