[NOI2015]軟體包管理器
題目描述
Linux使用者和OSX使用者一定對軟體包管理器不會陌生。通過軟體包管理器,你可以通過一行命令安裝某一個軟體包,然後軟體包管理器會幫助你從軟體源下載軟體包,同時自動解決所有的依賴(即下載安裝這個軟體包的安裝所依賴的其它軟體包),完成所有的配置。ebian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是優秀的軟體包管理器。
你決定設計你自己的軟體包管理器。不可避免地,你要解決軟體包之間的依賴問題。如果軟體包
現在你要為你的軟體包管理器寫一個依賴解決程式。根據反饋,使用者希望在安裝和解除安裝某個軟體包時,快速地知道這個操作實際上會改變多少個軟體包的安裝狀態(即安裝操作會安裝多少個未安裝的軟體包,或解除安裝操作會解除安裝多少個已安裝的軟體包),你的任務就是實現這個部分。注意,安裝一個已安裝的軟體包,或解除安裝一個未安裝的軟體包,都不會改變任何軟體包的安裝狀態,即在此情況下,改變安裝狀態的軟體包數為0。
輸入格式
從檔案manager.in中讀入資料。
輸入檔案的第1行包含1個整數
隨後一行包含
接下來一行包含1個整數
install
uninstall
你需要維護每個軟體包的安裝狀態,一開始所有的軟體包都處於未安裝狀態。
對於每個操作,你需要輸出這步操作會改變多少個軟體包的安裝狀態,隨後應用這個操作(即改變你維護的安裝狀態)。
輸出格式
輸出到檔案manager.out中。
輸出檔案包括
輸出檔案的第
輸入樣例#1
7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0
輸出樣例#1
3
1
3
2
3
輸入樣例#2
10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9
輸出樣例#2
1
3
2
1
3
1
1
1
0
1
樣例說明1
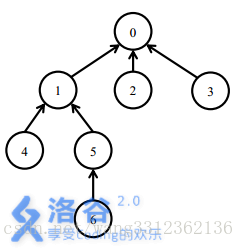
一開始所有的軟體包都處於未安裝狀態。
安裝5號軟體包,需要安裝0,1,5三個軟體包。
之後安裝6號軟體包,只需要安裝6號軟體包。此時安裝了0,1,5,6四個軟體包。
解除安裝1號軟體包需要解除安裝1,5,6三個軟體包。此時只有0號軟體包還處於安裝狀態。
之後安裝4號軟體包,需要安裝1,4兩個軟體包。此時0,1,4處在安裝狀態。最後,解除安裝0號軟體包會解除安裝所有的軟體包。`
資料範圍
思路
裸的樹鏈剖分啊。。。
注意一點:每一棵子樹的dfs序是連續的。
程式碼
#include <cstdio>
#include <algorithm>
const int maxn=100000;
struct sigment_tree
{
int val[(maxn<<2)+10],lazy[(maxn<<2)+10];
int updata(int now)
{
val[now]=val[now<<1]+val[now<<1|1];
return 0;
}
int pushdown(int now,int left,int right)
{
if(lazy[now]!=-1)
{
int mid=(left+right)>>1;
lazy[now<<1]=lazy[now];
val[now<<1]=(mid-left+1)*lazy[now];
lazy[now<<1|1]=lazy[now];
val[now<<1|1]=(right-mid)*lazy[now];
lazy[now]=-1;
}
return 0;
}
int build(int now,int left,int right)
{
lazy[now]=-1;
if(left==right)
{
val[now]=0;
return 0;
}
int mid=(left+right)>>1;
build(now<<1,left,mid);
build(now<<1|1,mid+1,right);
updata(now);
return 0;
}
int change(int now,int left,int right,int askl,int askr,int changeval)
{
if((askl>right)||(askr<left))
{
return 0;
}
if((askl<=left)&&(right<=askr))
{
int res=val[now];
if(changeval)
{
res=(right-left+1)-res;
}
lazy[now]=changeval;
val[now]=(right-left+1)*changeval;
return res;
}
pushdown(now,left,right);
int mid=(left+right)>>1;
int res=change(now<<1,left,mid,askl,askr,changeval)+change(now<<1|1,mid+1,right,askl,askr,changeval);
updata(now);
return res;
}
};
int n,m,ans;
struct tree
{
int pre[maxn+10],now[maxn+10],son[maxn+10],tot;
int deep[maxn+10],size[maxn+10],fa[maxn+10],wson[maxn+10],dfn[maxn+10],cnt,top[maxn+10];
sigment_tree st;
int mem()
{
st.build(1,0,n-1);
return 0;
}
int ins(int a,int b)
{
tot++;
pre[tot]=now[a];
now[a]=tot;
son[tot]=b;
fa[b]=a;
return 0;
}
int first_dfs(int u)
{
deep[u]=deep[fa[u]]+1;
size[u]=1;
int j=now[u];
while(j)
{
int v=son[j];
first_dfs(v);
size[u]+=size[v];
if((!wson[u])||(size[wson[u]]<size[v]))
{
wson[u]=v;
}
j=pre[j];
}
return 0;
}
int second_dfs(int u,int topfather)
{
top[u]=topfather;
dfn[u]=cnt;
cnt++;
if(wson[u])
{
second_dfs(wson[u],topfather);
}
int j=now[u];
while(j)
{
int v=son[j];
if(v!=wson[u])
{
second_dfs(v,v);
}
j=pre[j];
}
return 0;
}
int query(int x,int kind)
{
if(kind)
{
while(top[x]!=0)
{
ans+=st.change(1,0,n-1,dfn[top[x]],dfn[x],1);
x=fa[top[x]];
}
ans+=st.change(1,0,n-1,0,dfn[x],1);
}
else
{
ans+=st.change(1,0,n-1,dfn[x],dfn[x]+size[x]-1,0);
}
return 0;
}
};
tree t;
int main()
{
scanf("%d",&n);
t.mem();
for(int i=1; i<n; i++)
{
int a;
scanf("%d",&a);
t.ins(a,i);
}
t.first_dfs(0);
t.second_dfs(0,0);
scanf("%d",&m);
for(int i=1; i<=m; i++)
{
ans=0;
char opt[10];
int a;
scanf("%s%d",opt,&a);
if(opt[0]=='i')
{
t.query(a,1);
}
else
{
t.query(a,0);
}
printf("%d\n",ans);
}
return 0;
}