hdu1693 插頭dp
阿新 • • 發佈:2019-02-01
學習插頭dp 真是艱難,做的第一道題。
題意,現在給一個n*m的矩陣 矩陣中有一些障礙,障礙不能通過,現在要把能通過的點全部連起來,形成哈密頓迴路,但是可以連成多個哈密頓迴路,問有多少種方法。
直接說做法吧,首先是用輪廓線不懂的,可以先看看這
看圖

在輪廓線上每一位如果有一個插頭那麼這一位就表示位1沒有就表示為0,插頭是是在迴路上的線,如果有插頭表示上一格經過了這一條邊,如圖狀態表示為101111當前轉移的格子為第二行第三個,轉移的時候主要看這個格子左邊和上面的插頭,如果都為1表示這兩個連線到一起了,如果其中一個格子為1另一個為0 那麼就是有兩個出口如圖,注意一下如果當前格子是障礙的話要特殊處理一下,只有在上插頭和左插頭是0的時候才能轉移,因為沒有辦法經過這個格子
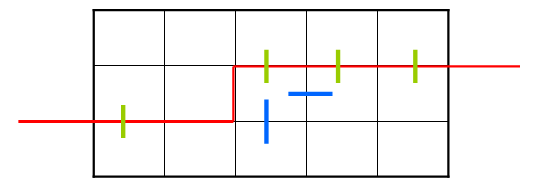
然後特殊處理一下最後一格,一行處理完後要把輪廓線移動到前面來,如圖

具體操作看程式碼:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<string>
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
#define LL long long 