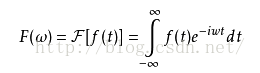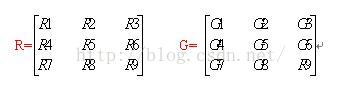數字影象處理2--數學基礎(傅立葉,拉普拉斯,卷積,差分計算)
本文是為了方便各位在影象處理中理解基本的數學模型及其表示式等,所以我們不對該類數學基礎在訊號與系統等方面的運用。歡迎評論補充!
影象的頻率是表徵影象中灰度變化劇烈程度的指標,是灰度在平面空間上的梯度。 如:大面積的沙漠在影象中是一片灰度變化緩慢的區域,對應的頻率值很低;而對於地表屬性變換劇烈的邊緣區域在影象中是一片灰度變化劇烈的區域,對應的頻率 值較高。傅立葉變換在實際中有非常明顯的物理意義,設f是一個能量有限的模擬訊號,則其傅立葉變換就表示f的譜。從純粹的數學意義上看,傅立葉變換是將一
個函式轉換為一系列周期函式來處理的。從物理效果看,傅立葉變換是將影象從空間域轉換到頻率域,其逆變換是將影象從頻率域轉換到空間域。換句話說,傅立葉 變換的物理意義是將影象的灰度分佈函式變換為影象的頻率分佈函式傅立葉變換
週期性連續訊號 傅立葉級數(Fourier Series)非週期性連續訊號 傅立葉變換(Fourier Transform)
非週期性離散訊號 離散時域傅立葉變換(Discrete Time Fourier Transform)
週期性離散訊號 離散傅立葉變換(Discrete Fourier Transform) -DFT
若 f(t)是t的周期函式,如果t滿足狄裡赫萊條件:在一個以2T為週期內f(X)連續或只有有限個第一類間斷點,附f(x)單調或可劃分成有限個單調區間,則F(x)以2T為週期的傅立葉級數收斂,和函式S(x)也是以2T為週期的周期函式,且在這些間斷點上,
傅立葉變換可以化複雜的卷積運算為簡單的乘積運算,從而提供了計算卷積的一種簡單手段。
線性性質

對偶性
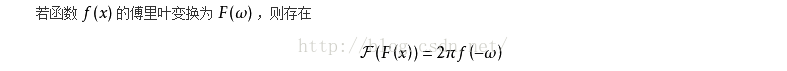 。
。
微分關係

時域卷積定理

頻域卷積定理
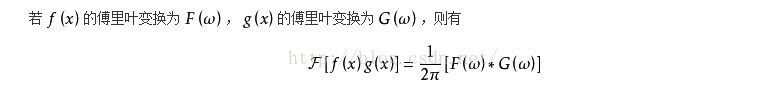
離散傅立葉變換

快速傅立葉變換
它是利用計算機計算離散傅立葉變換(DFT)的高效、快速計算方法的統稱,主要改善了離散傅立葉變換的複雜度。FFT(快速傅立葉變換)本身就是離散傅立葉變換(Discrete Fourier Transform)的快速演算法,使演算法複雜度由原本的O(N^2) 變為 O(NlogN)。具體演算法不必深究,有需要再去了解。二維傅立葉變換
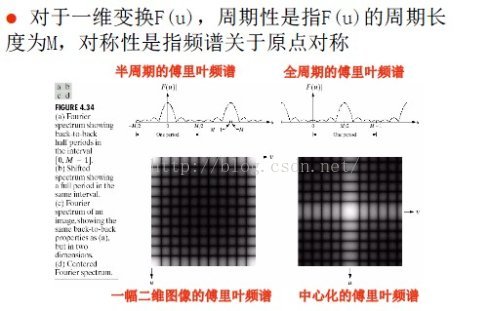
二維傅立葉變換一般用在數字影象處理中,一般是二維的灰度影象f(x,y)變換到頻域F(u,v)。在頻譜圖中,中心部分(uv座標系中點(0,0)附近)表示原影象中的低頻部分,是影象中灰度變化不太快的成分,反映了影象的主體框架;而頻譜的四周,也即是高頻區域是影象中灰度變化較快的成分,一般反映著影象中的椒鹽噪聲(突發性的白點或黑點)或者是影象內部變化劇烈的邊緣成分。如果原始影象具有十分明顯的規律,例如將一個簡單圖樣有規律的平移並填滿整個圖形,那麼其頻譜一般表現為座標原點周圍的一圈亮點。
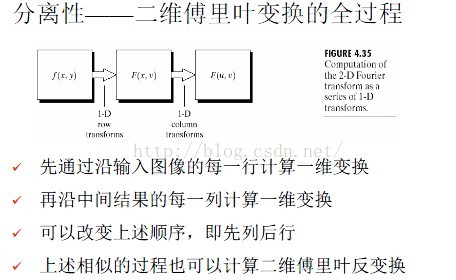
根據一維離散傅立葉變換,直接給出二維DFT的公式,這個公式的具體程式碼實現在前面文章中有提到,但是實際中由於DFT計算速度過慢,普遍使用FFT作為快速演算法,DFT和IDFT的公式如下: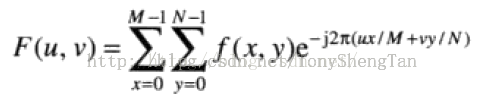
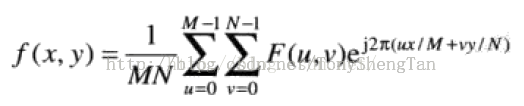
二維DFT公式的推導過程與一維相同,對連續傅立葉變換進行取樣或者是將原始資料週期複製後計算傅立葉級數,然後取主值,在此不再贅述。





常見性質


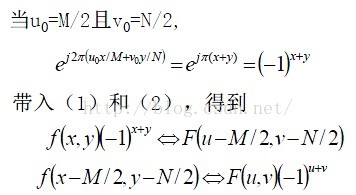










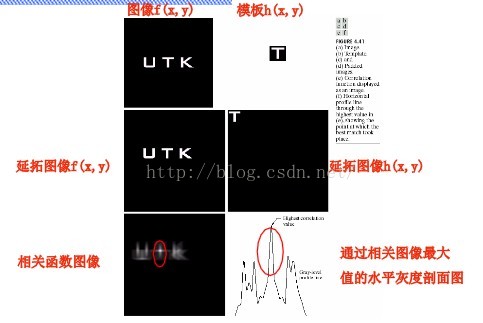
卷積和相關理論
卷積運算:可看作是加權求和的過程,使用到的影象區域中的每個畫素分別與卷積核(權矩陣)的每個元素對應相乘,所有乘積之和作為區域中心畫素的新值。卷積核:卷積時使用到的權,用一個矩陣表示,該矩陣與使用的影象區域大小相同,其行、列都是奇數,是一個權矩陣。
1、卷積示例:
假設3 * 3的畫素區域R與卷積核G分別為:
則卷積運算為:
R5(中心畫素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2、使用模板處理影象時涉及到的問題:
邊界問題:當處理影象邊界畫素時,卷積核與影象使用區域不能匹配,卷積核的中心與邊界畫素點對應,卷積運算將出現問題。
處理辦法:
A.忽略邊界畫素,即處理後的影象將丟掉這些畫素。
B.保留原邊界畫素,即copy邊界畫素到處理後的影象。
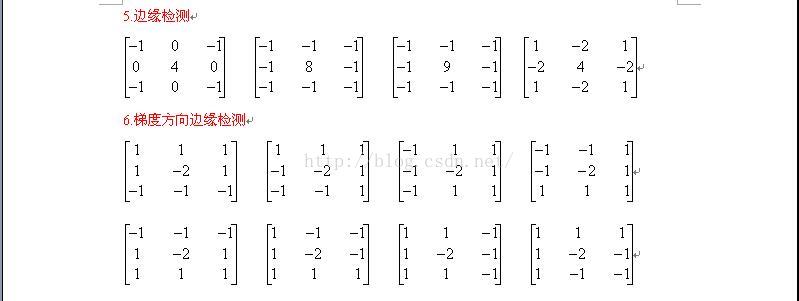
3、常用模板:
連續空間的卷積定義是f(x)與g(x)的卷積是f(t-x)g(x)在t從負無窮到正無窮的積分值.t-x要在f(x)定義域內,所以看上去很大的積分實際上還是在一定範圍的.
實際的過程就是f(x)先做一個Y軸的反轉,然後再沿X軸平移t就是f(t-x),然後再把g(x)拿來,兩者乘積的值再積分.想象一下如果g(x)或者f(x)是個單位的階越函式.那麼就是f(t-x)與g(x)相交部分的面積.這就是卷積了.
卷積運算滿足交換律,也就是說:f與g進行卷積完全等於g與f進行卷積。
由兩個函式f和g進行卷積而得到的函式f*g,一般要比原來的f和g都要光滑。所以在影象處理中對影象進行卷積後會使原影象模糊。
因為卷積具有平滑作用。
那麼在影象中卷積是什麼意思呢,就是影象就是影象f(x),模板是g(x),然後將模版g(x)在模版中移動,每到一個位置,就把f(x)與g(x)的定義域相交的元素進行乘積並且求和,得出新的影象一點,就是被卷積後的影象.模版又稱為卷積核.卷積核做一個矩陣的形狀。