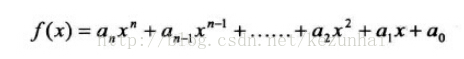多項式函式是變數的整數次冥與係數的乘積之和，可以用下面的公式表示：

由於多項式函式只包含加法和乘法運算，因此計算容易，並且可以用於計算其他數學函式的近似值。在Numpy中，多項式函式的係數可以用一維陣列表示，如f(x) =x^3-2x+1，則可以表示為陣列：

a = np.array([1.0,0,-2,1])

      係數可以通過poly1d( )函式轉換為多項式物件，此物件可以像函式一樣呼叫，它返回多項式函式的值，如：

>>> a = np.array([1.0,0,-2,1])
>>> p = np.poly1d(a)
>>> type(p)
<class 'numpy.lib.polynomial.poly1d'>
>>> p(np.linspace(0,1,5))
array([ 1.      ,  0.515625,  0.125   , -0.078125,  0.      ])
>>> 
 

>>> p+[-2,1] #和p+np.poly1d([-2,1])相同，-2x+1
poly1d([ 1.,  0., -4.,  2.])
>>> p*p #兩個3次多項式相乘，得到一個6次多項式
poly1d([ 1.,  0., -4.,  2.,  4., -4.,  1.])
>>> p/[1,1] #返回2個多項式除法的結果，分別為商式和餘式
(poly1d([ 1., -1., -1.]), poly1d([ 2.]))
>>> 
 

>>> p.deriv()
poly1d([ 3.,  0., -2.])
>>> p.integ()
poly1d([ 0.25,  0.  , -1.  ,  1.  ,  0.  ])

>>> r = np.roots(p)
>>> r
array([-1.61803399,  1.        ,  0.61803399])
>>> 
 

>>> np.poly(r)
array([  1.00000000e+00,  -1.22124533e-15,  -2.00000000e+00,
         1.00000000e+00])
>>>