Nim or not Nim?

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1076    Accepted Submission(s): 532


Problem Description Nim is a two-player mathematic game of strategy in which players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap.

Nim is usually played as a misere game, in which the player to take the last object loses. Nim can also be played as a normal play game, which means that the person who makes the last move (i.e., who takes the last object) wins. This is called normal play because most games follow this convention, even though Nim usually does not.

Alice and Bob is tired of playing Nim under the standard rule, so they make a difference by also allowing the player to separate one of the heaps into two smaller ones. That is, each turn the player may either remove any number of objects from a heap or separate a heap into two smaller ones, and the one who takes the last object wins.
Input Input contains multiple test cases. The first line is an integer 1 ≤ T ≤ 100, the number of test cases. Each case begins with an integer N, indicating the number of the heaps, the next line contains N integers s[0], s[1], ...., s[N-1], representing heaps with s[0], s[1], ..., s[N-1] objects respectively.(1 ≤ N ≤ 10^6, 1 ≤ S[i] ≤ 2^31 - 1)
Output For each test case, output a line which contains either "Alice" or "Bob", which is the winner of this game. Alice will play first. You may asume they never make mistakes.
Sample Input 2 3 2 2 3 2 3 3
Sample Output Alice Bob 由於資料範圍比較大，如果直接求SG函式的話，會MLE，，，但是我們可以先打表求出部分SG函式，然後找規律， SG打表程式碼：

#include <stdio.h>
#include <string.h>
#define MAX 50
int sg[MAX] ;
int getSG()
{
	bool visited[100] ;
	for(int i = 1 ; i < MAX ; ++i)
	{
		memset(visited,false,sizeof(visited)) ;
		for(int j = 1 ; j <= i ; ++j)
		{
			visited[sg[i-j]] = true ;
		}
		for(int j = 1 ; j < i ; ++j)
		{
			visited[sg[i-j]^sg[j]] = true ;
		}
		for(int j = 1 ; j < MAX ; ++j)
		{
			if(!visited[j])
			{
				sg[i] = j ;
				printf("%d %d\n",i,sg[i]) ;
				break ;
			}
		}
	}
}

int main()
{
	getSG() ;
	return 0 ;
}
 

打表結果：
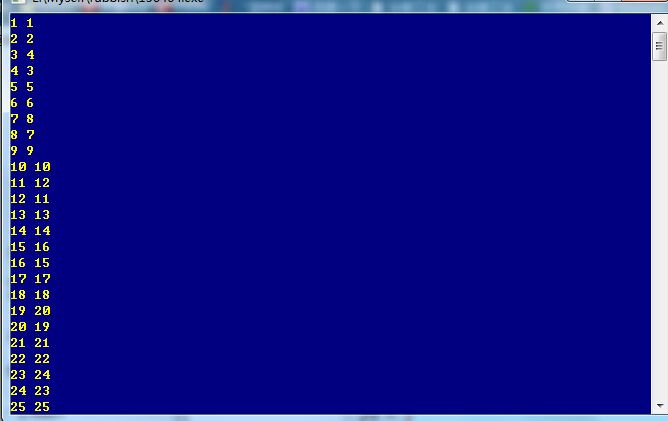
當x%4=1or2時，sg[x] = x,當x%4==3時，sg[x]=x+1,當x%4==0時，sg[x] = x-1； 所以這道題的程式碼為：

#include <stdio.h>
#include <limits.h>
int main()
{
	int t ;
	scanf("%d",&t) ;
	while(t--)
	{
		int n ,ans = 0;
		scanf("%d",&n);
		for(int i = 0 ; i < n ; ++i)
		{
			int temp ;
			scanf("%d",&temp);
			if(temp%4==1||temp%4==2)
			{
				ans ^= temp ;
			}
			else if(temp%4==3)
			{
				ans ^= temp+1;
			}
			else if(temp%4==0)
			{
				ans ^= temp-1 ;
			}
		}
		if(ans)
		{
			puts("Alice") ;
		}
		else
		{
			puts("Bob") ;
		}
	}
	return 0 ;
}