java實現二叉樹的Node節點定義,並手撕8種遍歷
最近準備秋招面試,發現二叉樹這種可以無限擴充套件知識點來虐別人的資料結構,很受面試官的青睞。
如果掌握的不好,會直接死在一面哦。
怕嗎?當你原理、思想,內部結構通通明白,分分鐘手撕程式碼的程度,還怕嗎?
本篇文章就從用java的思想和程式從最基本的怎麼將一個int型的陣列變成Node樹狀結構說起,再到遞迴前序遍歷,遞迴中序遍歷,遞迴後序遍歷,非遞迴前序遍歷,非遞迴前序遍歷,非遞迴前序遍歷,到最後的廣度優先遍歷和深度優先遍歷
你想要的都在這裡,是不是很貼心! 【麼麼】
來咯!
一、Node節點的java實現
首先在可以看到打上Node這個字串,就可以看到只能的IDEA系統提供的好多提示:
點進去看,卻不是可以直接構成二叉樹的Node,不是我們需要的東西。這裡舉個例子來看
org.w3c.dom
這裡面的Node是一個介面,是解析XML時的文件樹。在官方文件裡面看出:該 Node 介面是整個文件物件模型的主要資料型別。它表示該文件樹中的單個節點。當實現 Node 介面的所有物件公開處理子節點的方法時,不是實現 Node 介面的所有物件都有子節點。
所以我們需要自定義一個Node類
package com.sort.text; public class Node { private int value; //節點的值 private Node node; //此節點,資料型別為Node private Node left; //此節點的左子節點,資料型別為Node private Node right; //此節點的右子節點,資料型別為Node public int getValue() { return value; } public void setValue(int value) { this.value = value; } public Node getNode() { return node; } public void setNode(Node node) { this.node = node; } public Node getLeft() { return left; } public void setLeft(Node left) { this.left = left; } public Node getRight() { return right; } public void setRight(Node right) { this.right = right; } public Node(int value) { this.value=value; this.left=null; this.right=null; } public String toString() { //自定義的toString方法,為了方便之後的輸出 return this.value+" "; } }
定義好了之後就可以開始直接使用了,相信大家都可以秒看懂。
二、陣列昇華二叉樹
一般拿到的資料是一個int型的陣列,那怎麼將這個陣列變成我們可以直接操作的樹結構呢?
1、陣列元素變Node型別節點
2、給N/2-1個節點設定子節點
3、給最後一個節點設定子節點【有可能只有左節點】
那現在就直接上程式碼
public static void create(int[] datas,List<Node> list) { //將數組裡面的東西變成節點的形式 for(int i=0;i<datas.length;i++) { Node node=new Node(datas[i]); list.add(node); } //節點關聯成樹 for(int index=0;index<list.size()/2-1;index++) { list.get(index).setLeft(list.get(index*2+1)); //編號為n的節點他的左子節點編號為2*n 右子節點編號為2*n+1 但是因為list從0開始編號,所以還要+1 list.get(index).setRight(list.get(index*2+2)); //與上同理 } //單獨處理最後一個父節點 ,list.size()/2-1進行設定,避免單孩子情況 int index=list.size()/2-1; list.get(index).setLeft(list.get(index*2+1)); if(list.size()%2==1) //如果有奇數個節點,最後一個父節點才有右子節點 list.get(index).setRight(list.get(index*2+2)); }
很細緻的加上了很多的註釋啊,所以保證一看就懂。
開始大招前的攢金幣過程正式結束
現在開始放大招
三、遞迴前序遍歷
具體的原理沒有什麼好講的,知道順序即可
先序遍歷過程:
(1)訪問根節點;
(2)採用先序遞迴遍歷左子樹;
(3)採用先序遞迴遍歷右子樹;
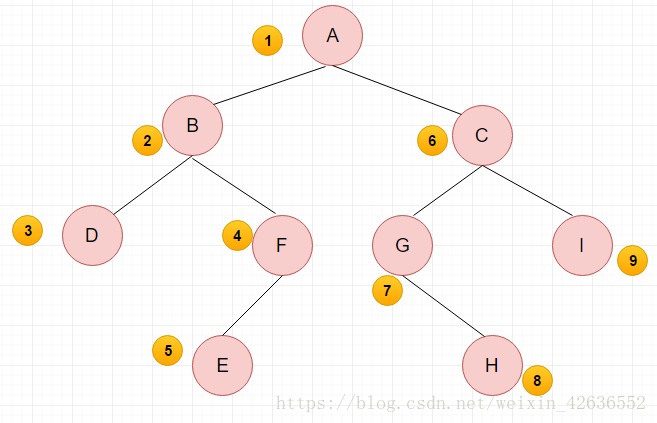
這裡用圖來說明
先序遍歷結果:A BDFE CGHI
還是看程式碼吧
public void preTraversal(Node node){
if (node == null) //很重要,必須加上 當遇到葉子節點用來停止向下遍歷
return;
System.out.print(node.getValue()+" ");
preTraversal(node.getLeft());
preTraversal(node.getRight());
}
看,說了很簡單吧!
四、遞迴中序遍歷
中序遍歷:
(1)採用中序遍歷左子樹;
(2)訪問根節點;
(3)採用中序遍歷右子樹
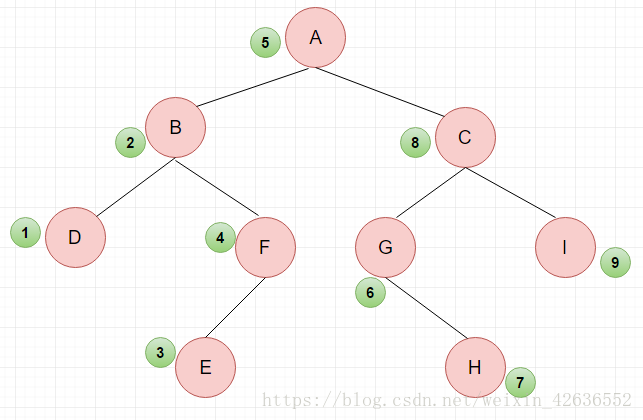
中序遍歷結果:DBEF A GHCI
有請程式碼:
public void MidTraversal(Node node){
if (node == null)
return;
MidTraversa(node.getLeft());
System.out.print(node.getValue()+" ");
MidTraversa(node.getRight());
}
五、遞迴後序遍歷
後序遍歷:
(1)採用後序遞迴遍歷左子樹;
(2)採用後序遞迴遍歷右子樹;
(3)訪問根節點;
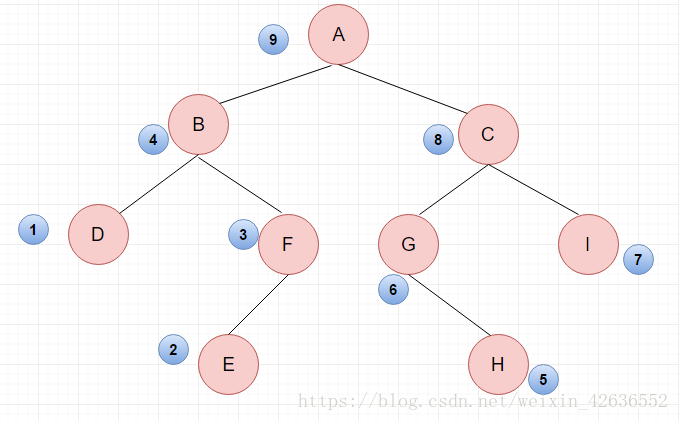
後序遍歷的結果:DEFB HGIC A
程式碼:
public void postTraversal(Node node){
if (node == null)
return;
postTraversal(node.getLeft());
postTraversal(node.getRight());
System.out.print(node.getValue()+" ");
}
其實程式碼和思想一樣,只是輸出的位置和遞迴呼叫的位置不同而已。
個人覺得懂得非遞迴的原理和程式碼比懂遞迴更有意思,當你能手撕非遞迴二叉樹遍歷的時候,面試官問你原理,還能不知道嗎?
那接下來的三個模組就是非遞迴的三種遍歷
拭目以待
六、非遞迴前序遍歷
我這裡使用了棧這個資料結構,用來儲存不到遍歷過但是沒有遍歷完全的父節點
之後再進行回滾。
基本的原理就是當迴圈中的p不為空時,就讀取p的值,並不斷更新p為其左子節點,即不斷讀取左子節點,直到一個枝節到達最後的子節點,再繼續返回上一層進行取值
程式碼:
public void preOrderTraversalbyLoop(Node node){
Stack<Node> stack = new Stack();
Node p = node;
while(p!=null || !stack.isEmpty()){
while(p!=null){
//當p不為空時,就讀取p的值,並不斷更新p為其左子節點,即不斷讀取左子節點
System.out.print(p.getValue()+" ");
stack.push(p); //將p入棧
p = p.getLeft();
}
if(!stack.isEmpty()){
p = stack.pop();
p = p.getRight();
}
}
}
執行結果,很順利的得到想要的結果
七、非遞迴中序遍歷
同原理
就是當迴圈中的p不為空時,就讀取p的值,並不斷更新p為其左子節點,但是切記這個時候不能進行輸出,必須不斷讀取左子節點,直到一個枝節到達最後的子節點,然後每次從棧中拿出一個元素,就進行輸出,再繼續返回上一層進行取值
程式碼如下:
public void inOrderTraversalbyLoop(Node node){
Stack<Node> stack = new Stack();
Node p = node;
while(p!=null || !stack.isEmpty()){
while(p!=null){
stack.push(p);
p = p.getLeft();
}
if(!stack.isEmpty()){
p = stack.pop();
System.out.print(p.getValue()+" ");
p = p.getRight();
}
}
}
八、非遞迴後序遍歷
後序遍歷相比前面的前序遍歷和中序遍歷在程式設計這裡會難一點,不過理解了思想,看程式碼還是沒有什麼問題的
public void postOrderTraversalbyLoop(Node node){
Stack<Node> stack = new Stack<Node>();
Node p = node, prev = node;
while(p!=null || !stack.isEmpty()){
while(p!=null){
stack.push(p);
p = p.getLeft();
}
if(!stack.isEmpty()){
Node temp = stack.peek().getRight();
//只是拿出來棧頂這個值,並沒有進行刪除
if(temp == null||temp == prev){
//節點沒有右子節點或者到達根節點【考慮到最後一種情況】
p = stack.pop();
System.out.print(p.getValue()+" ");
prev = p;
p = null;
}
else{
p = temp;
}
}
}
}
最後就可以放大招了,來看看廣度優先遍歷和深度優先遍歷吧
九、廣度優先遍歷
public void bfs(Node root){
if(root == null) return;
LinkedList<Node> queue = new LinkedList<Node>();
queue.offer(root); //首先將根節點存入佇列
//當佇列裡有值時,每次取出隊首的node列印,列印之後判斷node是否有子節點,若有,則將子節點加入佇列
while(queue.size() > 0){
Node node = queue.peek();
queue.poll(); //取出隊首元素並列印
System.out.print(node.var+" ");
if(node.left != null){ //如果有左子節點,則將其存入佇列
queue.offer(node.left);
}
if(node.right != null){ //如果有右子節點,則將其存入佇列
queue.offer(node.right);
}
}
}
九、深度優先遍歷
public void dfs(Node node,List<List<Integer>> rst,List<Integer> list){
if(node == null) return;
if(node.left == null && node.right == null){
list.add(node.var);
/* 這裡將list存入rst中時,不能直接將list存入,而是通過新建一個list來實現,
* 因為如果直接用list的話,後面remove的時候也會將其最後一個存的節點刪掉
* */
rst.add(new ArrayList<>(list));
list.remove(list.size()-1);
}
list.add(node.var);
dfs(node.left,rst,list);
dfs(node.right,rst,list);
list.remove(list.size()-1);
}
------------------------------------------------------未完待續哦-----------------------------