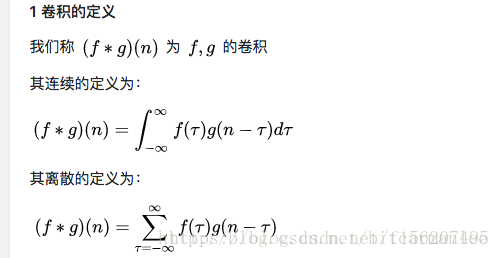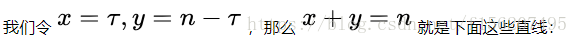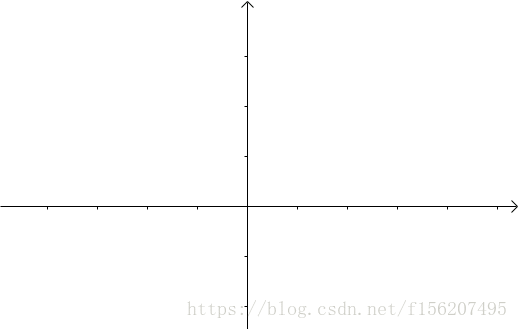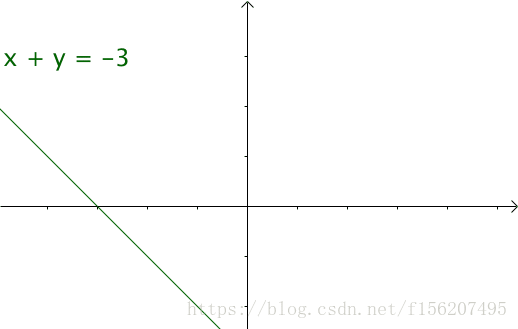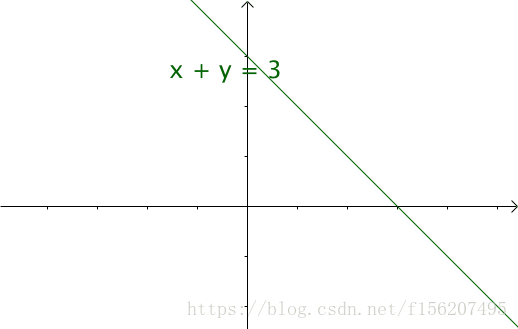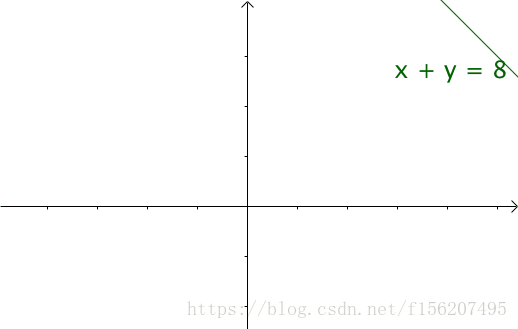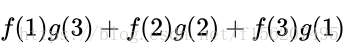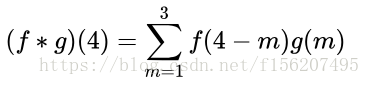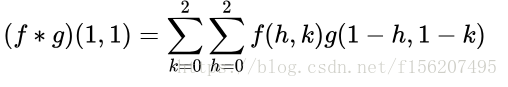用生動的例子來解釋卷積
前言
學了幾周的深度學習,前幾天感覺基礎不太牢固,於是今天便從卷積神經網路開始複習,把腦子中不太清楚的概念全部弄清楚。先在這裡說清楚,本文大部分例子都是參考其他的部落格,在某些例子中有些許改動,穿插著我自己的理解。
1. 從捲毛巾開始理解卷積
首先看看卷積的定義:
這兩個定義都有一個共同的特徵:
讓n不斷變化,得到下面動圖裡面的直線:
如果遍歷這些直線,就好比,把毛巾沿著角捲起來並積分(也相當於求和):
2. 藉助訊號系統來理解上面的卷積
其實我也沒有學過訊號系統,不過就常識來講,系統的響應強度不僅與當前時間t的輸入有關,還與前幾個時刻等若干個時刻的輸入有關。
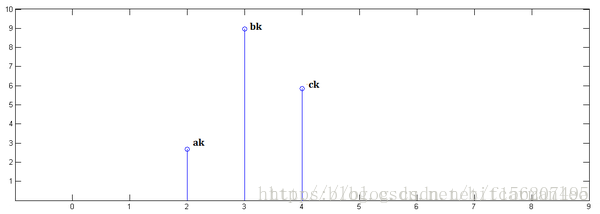
舉一個例子:假設任一時刻的輸入不僅會影響到的系統響應強度,而且還會影響後面兩個時刻的系統響應強度,並且影響權重分別為{a,b,c},現在分別給出時刻的輸入為,那麼如何求出時刻系統的響應強度呢?
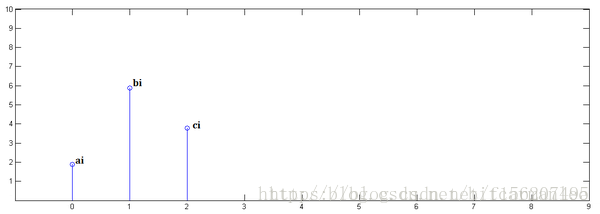
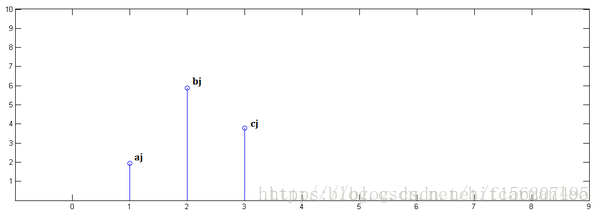
其實這個和上面講到的捲毛巾例子就很像,每一時刻的輸入會和後面的輸入產生疊加效應。下面給出幾張圖代表求解過程。
第一步:
,即;
,即;
,即;
第二步:
,即;
,即;
,即;
第三步:
,即;
,即;
,即;
第四步:
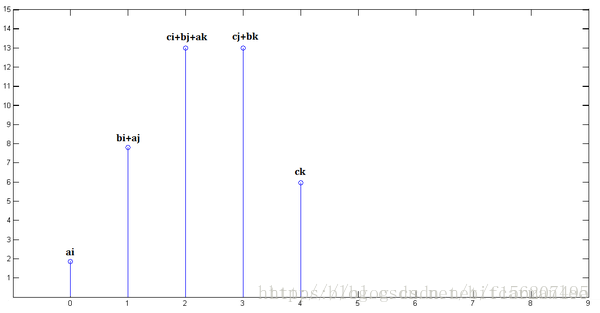
最後將各個時刻的結果累加起來就得到了下面的圖
相信你們看了這個例子之後會對前面的卷積公式有很好的理解。從上面那個例子來講,卷積就是將各個不同時刻輸入對某一時刻產生不同的影響疊加的過程。
3. 更多的例子
投骰子
假設我有兩枚骰子:
把這兩枚骰子都丟擲去
求:
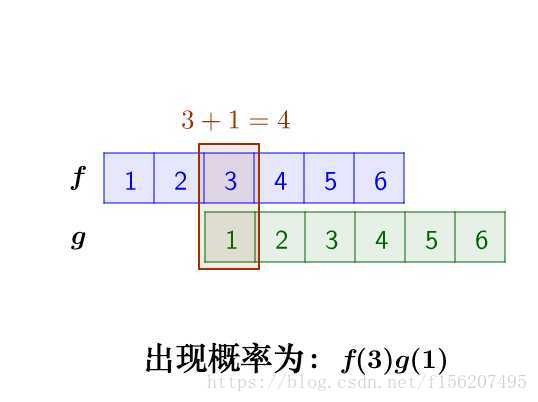
這裡問題的關鍵是,兩個骰子加起來要等於4,這正是卷積的應用場景。
我們把骰子各個點數出現的概率表示出來:
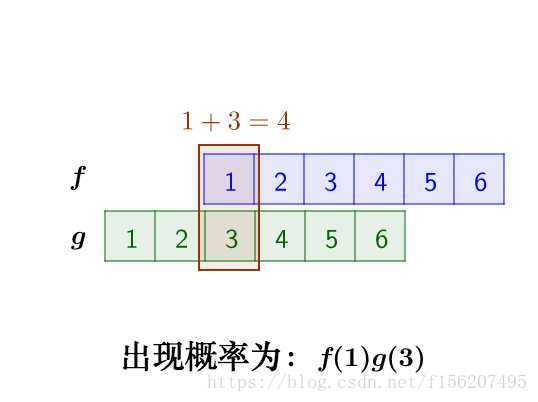
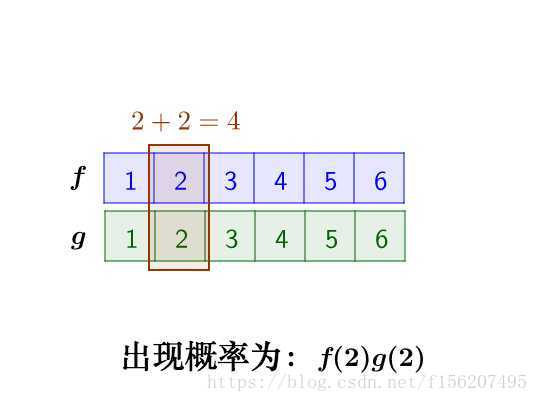
那麼,兩枚骰子點數加起來為4的情況有
因此,兩枚骰子點數加起來為4的概率為:
符合卷積的定義,把它寫成標準的形式就是:
做饅頭
鑽木取火
在生活當中有很多現象都體現了卷積的含義,比如古人鑽木取火就是一個很形象的例子。當我們用一根木頭與另一根木頭接觸並鑽一下,由於摩擦產生熱,在兩根木頭接觸的地方就會發熱,但是很明顯,就只鑽一下,木頭是不可能燃起來的,而且隨著時間變長,那一點由摩擦產生的熱量會一點一點消失掉。妙果我們加快鑽的頻率,也就是在之前所鑽出來的熱量還沒有消失掉的時候再多鑽幾下,把之前所有的殘餘的熱量疊加起來,時間越短,殘餘的熱量就會越多,這樣熱量就會在發熱的地方積累得很多,木頭的溫度也就會越來越高,最後達到著火點而燃燒起來。對於這個例子,其中有幾個關鍵的地方,第一,每一次鑽出來的熱量消失的速度快慢是由環境客觀條件比如溫度,和木頭的導熱係數所決定的。第二,我們認定木頭是一個線性系統,也就是對於幾任意兩次鑽的過程互不影響,只存在疊加關係。而且對於每一次不同程度的鑽所產生的熱量是與鑽的程度成正比的。
我們可以把這個問題抽象為一個數學模型:
鑽的過程為輸入x(t), 系統的衰減函式為h(t),木頭被鑽的地方積累的熱量為y(t)。在某個時間點u,鑽所產生的輸入為x(u),此時的衰減係數為h(t-u)為什麼是t-u呢?衰減函式接受的引數是經歷的衰減時間,從u到t還要經歷t-u這麼長時間的衰減,所以就要用t-u了,對x(u)h(t-u)du做個積分就得到y(t) 了。
也就是卷積表達了系統對於輸入的累計效應。
影象處理
4.1 原理:
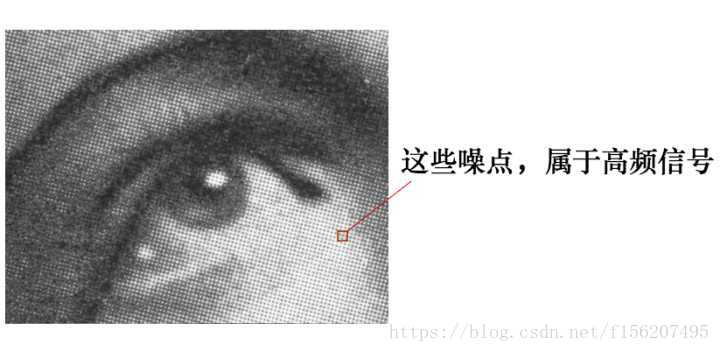
有這麼一副影象,可以看到,影象上有很多噪點:
高頻訊號,就好像平地聳立的山峰:
看起來很顯眼。
平滑這座山峰的辦法之一就是,把山峰刨掉一些土,填到山峰周圍去。用數學的話來說,就是把山峰周圍的高度平均一下。
平滑後得到:
4.2
卷積可以幫助實現這個平滑演算法。
有噪點的原圖,可以把它轉為一個矩陣:
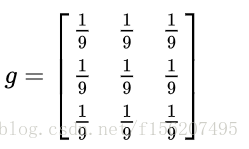
然後用下面這個平均矩陣(說明下,原圖的處理實際上用的是正態分佈矩陣,這裡為了簡單,就用了算術平均矩陣)來平滑影象:
記得剛才說過的演算法,把高頻訊號與周圍的數值平均一下就可以平滑山峰。
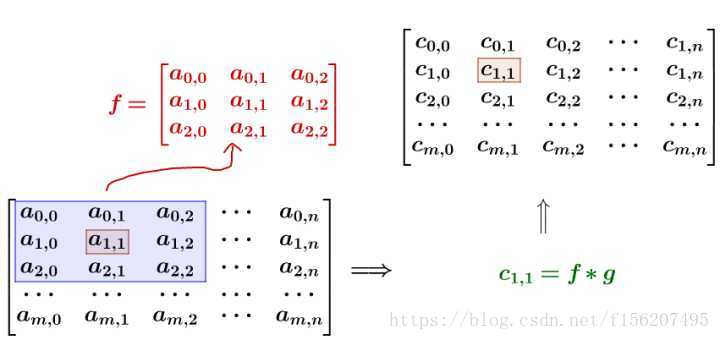
比如我要平滑 點,就在矩陣中,取出 點附近的點組成矩陣 ,和 進行卷積計算後,再填回去:
要注意一點,為了運用卷積, g 雖然和 f 同維度,但下標有點不一樣:
我用一個動圖來說明下計算過程:
寫成卷積公式就是:
要求 ,一樣可以套用上面的卷積公式。
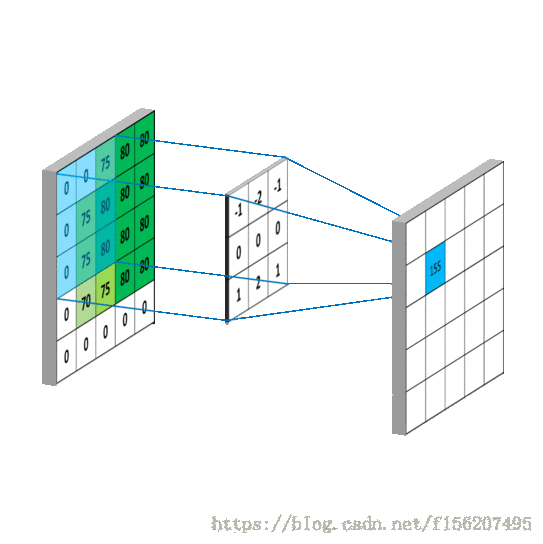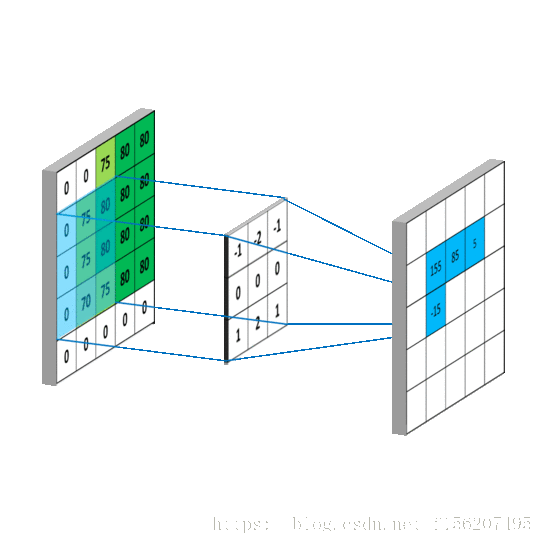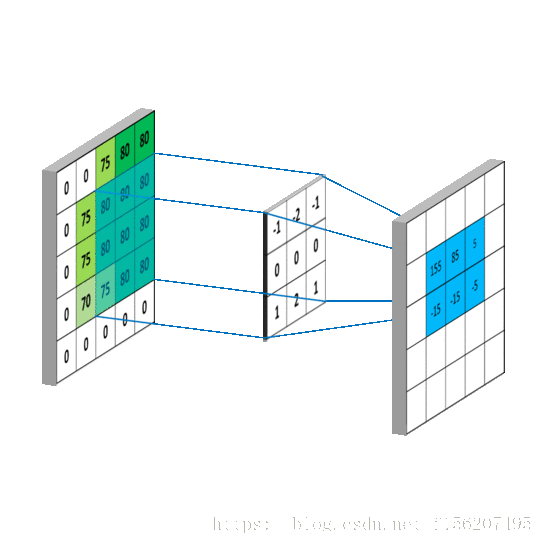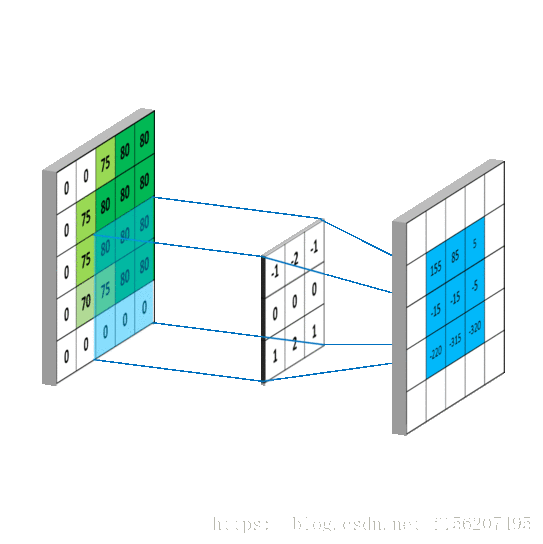
這樣相當於實現了 這個矩陣在原來影象上的划動(準確來說,下面這幅圖把 g 矩陣旋轉了 ):
4. 另外一個關於卷積的有意思的解釋
看了好多關於卷積的答案,看到這個例子才徹底地理解了這個過程~
關於卷積的一個血腥的講解
比如說你的老闆命令你幹活,你卻到樓下打檯球去了,後來被老闆發現,他非常氣憤,扇了你一巴掌(注意,這就是輸入訊號,脈衝),於是你的臉上會漸漸地(賤賤地)鼓起來一個包,你的臉就是一個系統,而鼓起來的包就是你的臉對巴掌的響應,好,這樣就和訊號系統建立起來意義對應的聯絡。下面還需要一些假設來保證論證的嚴謹:假定你的臉是線性時不變系統,也就是說,無論什麼時候老闆打你一巴掌,打在你臉的同一位置(這似乎要求你的臉足夠光滑,如果你說你長了很多青春痘,甚至整個臉皮處處連續處處不可導,那難度太大了,我就無話可說了哈哈),你的臉上總是會在相同的時間間隔內鼓起來一個相同高度的包來,並且假定以鼓起來的包的大小作為系統輸出。好了,那麼,下面可以進入核心內容——卷積了!
如果你每天都到地下去打檯球,那麼老闆每天都要扇你一巴掌,不過當老闆打你一巴掌後,你5分鐘就消腫了,所以時間長了,你甚至就適應這種生活了……如果有一天,老闆忍無可忍,以0.5秒的間隔開始不間斷的扇你的過程,這樣問題就來了,第一次扇你鼓起來的包還沒消腫,第二個巴掌就來了,你臉上的包就可能鼓起來兩倍高,老闆不斷扇你,脈衝不斷作用在你臉上,效果不斷疊加了,這樣這些效果就可以求和了,結果就是你臉上的包的高度隨時間變化的一個函數了(注意理解);如果老闆再狠一點,頻率越來越高,以至於你都辨別不清時間間隔了,那麼,求和就變成積分了。可以這樣理解,在這個過程中的某一固定的時刻,你的臉上的包的鼓起程度和什麼有關呢?和之前每次打你都有關!但是各次的貢獻是不一樣的,越早打的巴掌,貢獻越小,所以這就是說,某一時刻的輸出是之前很多次輸入乘以各自的衰減係數之後的疊加而形成某一點的輸出,然後再把不同時刻的輸出點放在一起,形成一個函式,這就是卷積,卷積之後的函式就是你臉上的包的大小隨時間變化的函式。本來你的包幾分鐘就可以消腫,可是如果連續打,幾個小時也消不了腫了,這難道不是一種平滑過程麼?反映到劍橋大學的公式上,f(a)就是第a個巴掌,g(x-a)就是第a個巴掌在x時刻的作用程度,乘起來再疊加就ok了,大家說是不是這個道理呢?我想這個例子已經非常形象了,你對卷積有了更加具體深刻的瞭解了嗎?