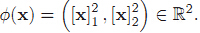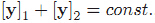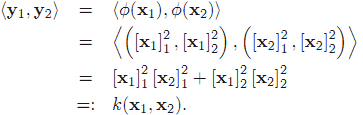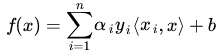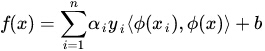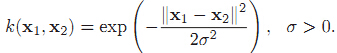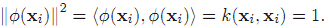機器學習 徑向基(Radial basis function)與RBF核函式 淺析
徑向基函式(RBF)在神經網路領域扮演著重要的角色，如 RBF神經網路具有唯一最佳逼近的特性，徑向基作為核函式在SVM中能將輸入樣本對映到高維特徵空間，解決一些原本線性不可分的問題。
本文主要討論：
1. 先討論核函式是如何把資料對映到高維空間的，然後引入徑向基函式作核函式，並特別說明高斯徑向基函式的幾何意義，以及它作為核函式時為什麼能把資料對映到無限維空間。
2.提到了徑向基函式，就繼續討論下徑向基函式神經網路為什麼能用來逼近。
注：核函式是一回事，徑向基函式是另一回事。
核函式表示的是高維空間裡由於向量內積而計算出來的一個函式表示式(後面將見到)。
徑向基函式是一類函式，徑向基函式是一個它的值(y)只依賴於變數(x)距原點距離的函式，即
；也可以是距其他某個中心點的距離，即
。也就是說，可以選定徑向基函式來當核函式，譬如SVM裡一般都用高斯徑向基作為核函式，但是核函式不一定要選擇徑向基這一類函式。
一.由非線性對映引入核函式概念，之後介紹高斯徑向基及其幾何意義。
預先規定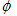
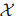
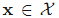
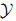
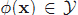
下面先用一個例子說明這種對映的好處。
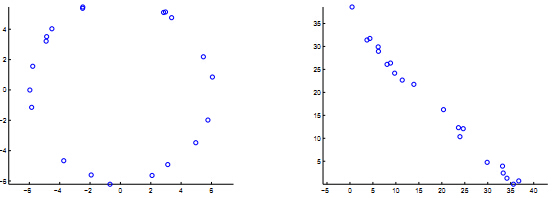
例：假設二維平面上有一些系列樣本點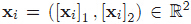 
如果設非線性對映為：
那麼在對映後的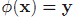
這意味著在新空間裡，樣本點是分佈在一條近似直線上的，而不是之前的圓，很明顯這利於線性可分。
圖1.左圖為原來的x所在的二維空間，右圖為對映後的新的y空間
繼續這個例子，我們已經知道了對映關係，那麼在 y 空間中的向量內積會是什麼樣子的呢？
注意公式裡的各種括號。[x]代表樣本 x ,圓括號 (,) 表示樣本的座標,尖括號 <,> 代表代表向量內積。
由此我們知道 y 空間裡兩向量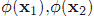 
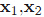
所以總結一下核函式就是：在原樣本空間中非線性問題，我們希望通過一種對映把他對映到高維空間裡使問題變得線性。然後在高維空間裡使用我們的演算法就能解決問題。而此時不用對映到高維只需非線性投影即可得到相同的效果。當然這裡按照前面的推導我們在高維空間裡的運算是以向量內積為基礎的。
回顧SVM裡的應用得到的分類器表示式為：
把x經過對映後得到的表示式為：
由此就可以看到這裡有高維空間裡的內積，就能夠用核函式代替這種內積了，而往往把高斯徑向基函式作為核函式。
高斯徑向基函式公式如下：
那麼它有什麼幾何意義呢。
先看看x經過對映以後，在高維空間裡這個點到原點的距離公式：
這表明樣本x對映到高維空間後，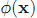
接下來將討論核函式為什麼能替代對映到高維空間，徑向基核又為什麼能夠對映到無限維空間。
先考慮普通的多項式核函式：
，其中
,並且 
.
因此這個多項式核函式能夠寫成：
.
現在回到之前的對映
並取 
，注意此時是3維空間了，那麼有
.
這就是前面的 k(x,y)，因此，該核函式就將2維對映到了3維空間。
看完了普通核函式由2維向3維的對映，再來看看高斯徑向基函式會把2維平面上一點對映到多少維。
呃，看看它的泰勒展開式你就會恍然大悟：
這個時候
(x)就是一個無限維的了。
二、RBF神經網路
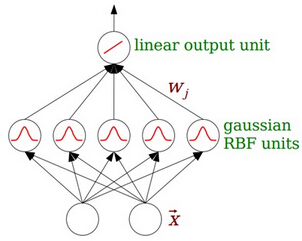
最基本的徑向基函式（RBF）神經網路的構成包括三層，其中每一層都有著完全不同的作用。輸入層由一些感知單元組成，它們將網路與外界環境連線起來；第二層是網路中僅有的一個隱層，它的作用是從輸入空間到隱層空間之間進行非線性變換，在大多數情況下，隱層空間有較高的維數；輸出層是線性的，它為作用於輸入層的啟用模式提供響應。
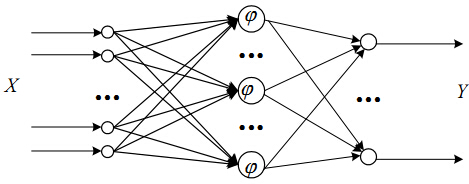
函式逼近的形式：
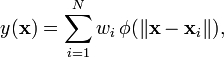
個人覺得，隱含層的每個節點就是就是空間中的一個基底，經過線性組合加權以後就變成了輸出。這種理解是通過逼近理論來理解的。
這裡的多項式P就是由基底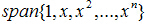
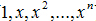
第二角度理解:
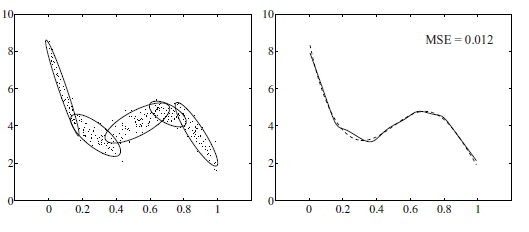
不知大家是否熟悉混合高斯模型，這裡的逼近有點像混合高斯模型。也就是每個高斯函式在自己的中心附近作出突出貢獻。
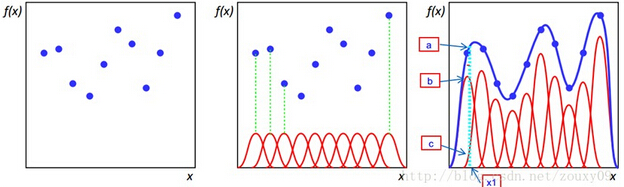
當年徑向基函式的誕生主要是為了解決多變數插值的問題。可以看下面的圖。具體的話是先在每個樣本上面放一個基函式，圖中每個藍色的點是一個樣本，然後中間那個圖中綠色虛線對應的，就表示的是每個訓練樣本對應一個高斯函式（高斯函式中心就是樣本點）。然後假設真實的擬合這些訓練資料的曲線是藍色的那根（最右邊的圖），如果我們有一個新的資料x1，我們想知道它對應的f(x1)是多少，也就是a點的縱座標是多少。那麼由圖可以看到，a點的縱座標等於b點的縱座標加上c點的縱座標。而b的縱座標是第一個樣本點的高斯函式的值乘以一個大點權值得到的，c的縱座標是第二個樣本點的高斯函式的值乘以另一個小點的權值得到。而其他樣本點的權值全是0，因為我們要插值的點x1在第一和第二個樣本點之間，遠離其他的樣本點，那麼插值影響最大的就是離得近的點，離的遠的就沒什麼貢獻了。所以x1點的函式值由附近的b和c兩個點就可以確定了。拓展到任意的新的x，這些紅色的高斯函式乘以一個權值後再在對應的x地方加起來，就可以完美的擬合真實的函式曲線了。
Reference：
1.Michael Eigensatz《Insights into the Geometry of the Gaussian Kernel and an Application in Geometric Modeling》
4.如果想學SVM, JerryLead 的 《支援向量機》系列 當然不能漏掉.
5.男神 Andrew Ng 的講義是師祖.