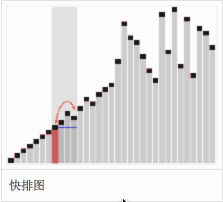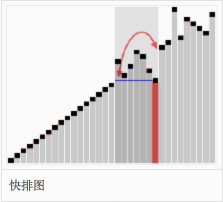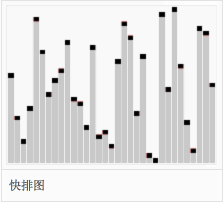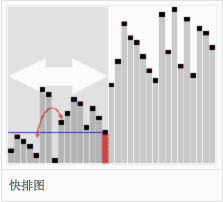
Quick Sort(快速排序)
演算法思想
通過快速排序將要排序的資料分為獨立的兩部分,其中一部分的資料比另外一部分的資料都要小,然後再按照此方法對這兩部分資料分別再進行快速排序,整個過程可以遞迴進行,以此達到整個序列都有序。快速排序和歸併排序是互補的:歸併排序將序列分成兩個子序列分別排序,並將有序的子序列歸併以將整個序列排序;而快速排序將序列排序的方式則是當兩個子序列都有序時整個序列也就自然有序了。前者遞迴呼叫發生在處理整個序列之前;後者的遞迴呼叫則發生在處理整個序列之後。在歸併排序中,一個序列被等分為兩半;在快速排序中,切分的位置取決於序列的位置。
實現步驟
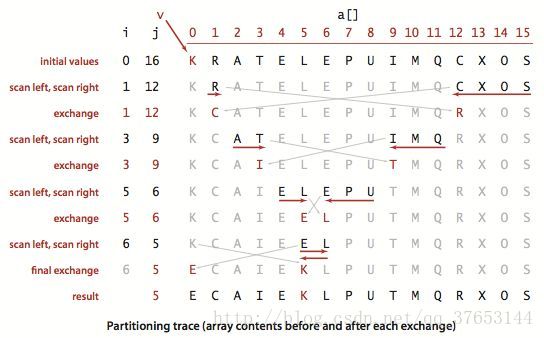
首先選取任意元素作為基準元素(一般是第一個元素),將所有比基準元素小的元素都排到其前面,比基準元素大的都排到其後面,這樣就完成了一趟快速排序。然後從基準元素分出的兩個子序列中再分別選出基準元素執行上述操作,直到不可再切分。
原始碼
C/C++
void QuickSort (int *a, int first, int last) { if (first < last) { int i = first, j = last, key = a[first]; while (i != j) { while (j > i && a[j] >= key) --j; a[i] = a[j]; while (i < j && a[i] <= key) ++i; a[j] = a[i]; } a[i] = key; QuickSort(a, first, i-1); QuickSort(a, i+1, last); } }
Python
def QuickSort(sequence, first, last): i, j = first, last if first < last: key = sequence[first] while i != j: while j > i and sequence[j] >= key: j -= 1 sequence[i] = sequence[j] while i < j and sequence[i] <= key: i += 1 sequence[j] = sequence[i] sequence[i] = key QuickSort(sequence, first, i-1) QuickSort(sequence, i+1, last)
時間複雜度
快速排序比較特殊,它相當依賴資料的隨機性。假設對一個已經排序好的序列進行排序,快速排序的時間複雜度將會退化到O(n²),這是最壞情況。而在最好情況下,每次都能將序列二等分,此時快速排序的時間複雜度為線性對數級O(nlog2n)。儘管不能保證每次切分都是等分,但即使這樣其平均效能相較於最好情況也相差不大(證明略)。因此保證資料的隨機性是維持快速排序時間複雜度的關鍵,在絕大部分情況下快速排序的執行時間都不會退化到n²級別。
效能特點
快速排序是原地排序的(只需要一個很小的輔助棧),且時間複雜度為線性對數級別,很好的將時間複雜度和空間複雜度都維持在一個較優的層級。另外,快速排序的內迴圈比大多數排序演算法都要簡單短小,這意味著快速排序無論是從理論上還是實際中都要更快。然而,快速排序的主要缺點是非常脆弱,在實現時要非常小心才能避免低劣的效能。
針對原始快速排序的缺點,擴展出許多快速排序的改進演算法,例如平衡快排、外部快排、三向切分快排、三路基數快排等等(可以另寫一篇文章了)。
穩定性
分析演算法原理可以知道,快速排序對相同元素不能維持最初的相對順序,因此快速排序是不穩定的排序。