題目

有一個正整數 a, 有 q 次詢問, 每次給定一個正整數 bi , 求 a^bi 的值. 由於答案可能很大, 你只需要輸出答案對 p 取模的結果。 又由於詢問可能很多, 給定一個引數 k, 你只需要輸出對於所有 k 的整數倍 i(0 < i ≤ q), 第一 次詢問到第 i 次詢問的結果的異或和. 為了防止輸入檔案過大, 每次詢問的值以以下方法生成: 設 bi 為第 i 次詢問的值, 給定 b0, l, m, c,i > 0 時,bi 滿足 bi = (m ∗ bi−1 + c)mod l

資料規模如下

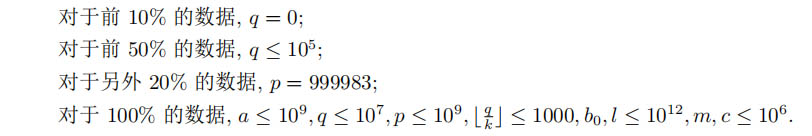
題解

直接模擬即可
對於$b_i$可以直接一個一個求，$O（N）$

程式碼

#include <cstdio>
#include <iostream>

using namespace std;

long long a,p,q,k,b0,l,m,c,b,ans;
long long ab[1000006],ba[1000006];

int main(){
	cin>>a>>p>>q>>k;
	cin>>b0>>l>>m>>c;
	ab[0]=1;
	for (int i=1;i<=1000000;i++)
		ab[i]=(ab[i-1]*a)%p;
	ba[0]=1;
	for (int i=1;i<=1000000;i++)
		ba[i]=(ba[i-1]*ab[1000000])%p;
	for (int i=1;i<=q;i++){
		b=(m*b0+c)%l;
		ans^=(ab[b%1000000]*ba[b/1000000])%p;
		b0=b;
		if (i%k==0&&i>=k) cout<<ans<<endl;
	}
}