一、DFS思想

本演算法以無向網為例，儲存方式採用鄰接連結串列

二、演算法複雜度：O(n+e)

        鄰接矩陣和鄰接表都是實現BFS和DFS的方法，鄰接矩陣時間複雜度為O(n^2)，鄰接表的時間複雜度為O(n+e)。因此鄰接矩陣適用於稠密圖，鄰接表適用於稀疏圖。

三、在實際編寫程式碼時，筆者發現

1）對採用鄰接連結串列作為儲存方式的圖做DFS時，由於建立鄰接連結串列時可採用不同的插入方法：比如頭插法和尾插法，會使得做DFS時相同的圖結構會有不一樣的結果；

2）即使相同的圖結構，採用不同的儲存方式（鄰接矩陣和鄰接連結串列）做DFS時，它們的結果有時也會不一樣；

筆者認為這都是正常現象，DFS的思想還是沒變。

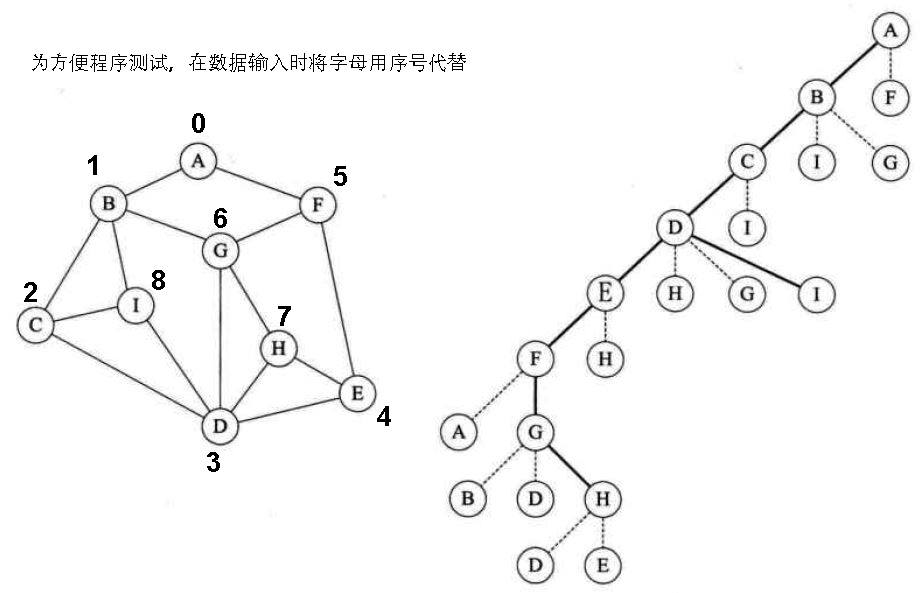
四、測試用例圖

本演算法的測試用例為《大話資料結構》p239中的圖7-5-2。如下圖所示：

五、C程式碼實現

/*******************************************************************************************
【DFS】
Author:tmw
date:2018-2-20
********************************************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>


#define MAX_VERTEX 100
#define inf 65535  //表示兩點之間沒有邊相連

int visit[MAX_VERTEX];   //標記頂點是否被訪問

/**無向圖的鄰接連結串列的建立**/
//邊表結點資料結構
typedef struct EdgeNode
{
    int adjvex;  //儲存該頂點對應的下標
    int weight;
    struct EdgeNode *next; //指向下一個鄰接點
}EdgeNode;

//頂點表結點資料結構
typedef struct VertexNode
{
    char Vertex;  //儲存頂點資訊
    EdgeNode *FistEdge; //邊表頭指標
}VertexNode,AdjList[MAX_VERTEX];

//鄰接連結串列圖的資料結構
typedef struct
{
    AdjList adjList;
    int VertexNumber,EdgeNumber; //頂點數和邊數
}GraphAdjList;


/**無向圖鄰接連結串列的建立**/
void Create_no_direction_LinkList_Graph(GraphAdjList *G)
{
    int i,j,w,k;
    printf("請輸入無向圖鄰接連結串列的頂點數和邊數：\n");
    scanf("%d %d",&G->VertexNumber,&G->EdgeNumber);

    //輸入頂點資訊，建立頂點表
    printf("頂點表的建立：輸入頂點資訊，如ABCDEF.....\n");
    char ch;
    while( ( ch = getchar()  != '\n' ) );
    for(i=0;i<G->VertexNumber;i++)
    {
        scanf("%c",&G->adjList[i].Vertex);
        G->adjList[i].FistEdge = NULL;
    }
    printf("邊表的建立：輸入邊（vi,vj）的頂點下標，權值統一為1，如：0 1 1(權值)\n");

    for(k=0;k<G->EdgeNumber;k++)
    {
        scanf("%d %d %d",&i,&j,&w);

        EdgeNode *e;
        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->weight = w;
        e->adjvex = j;
        e->next = G->adjList[i].FistEdge;   //頭插法將下標為j的頂點插入與之相連的下標為i的結點連結串列中
        G->adjList[i].FistEdge = e;

        //無向圖，因此是對稱的，同樣的操作將下標為i的頂點插入與之相連的下標為j的結點的連結串列中
        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->weight = w;
        e->adjvex = i;
        e->next = G->adjList[j].FistEdge;
        G->adjList[j].FistEdge = e;
    }


//    列印檢查
    printf("---------------------構造出來的無向圖鄰接連結串列的邊資訊如下---------------------\n");
    for(i=0;i<G->VertexNumber;i++)
    {
        EdgeNode *p;
        p = G->adjList[i].FistEdge;
        printf("%d\t",i);
        while(p != NULL)
        {
            printf("%d ",p->adjvex);
            p = p->next;
        }
        printf("\n");
    }
}

//無向圖的鄰接連結串列的第i個頂點的DFS
void DFS(GraphAdjList G, int i)
{
    visit[i] = true;
    printf("%c ",G.adjList[i].Vertex);

    EdgeNode *p;
    p = G.adjList[i].FistEdge;

    while(p)
    {
        if( !visit[p->adjvex] )
            DFS(G,p->adjvex);
        p = p->next;
    }
}

//對整個無向圖進行DFS
void DFS_Travel(GraphAdjList G)
{
    int i;

    //先初始化visit陣列
    for(i=0;i<G.VertexNumber;i++)
        visit[i] = false;

    printf("無向圖的鄰接連結串列DFS結果為：\n");
    for(i=0;i<G.VertexNumber;i++)
        if(!visit[i])
            DFS(G,i);
}

 

六、測試程式碼及測試結果

int main()
{
    printf("測試程式碼\n");
    GraphAdjList G;
    Create_no_direction_LinkList_Graph(&G);
    DFS_Travel(G);
    return 0;
}

測試結果如下：