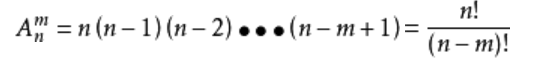一．                                 全排列演算法

首先：什麼是全排列=》百度一下

從n個不同元素中任取m（m≤n）個元素，按照一定的順序排列起來，叫做從n個不同元素中取出m個元素的一個排列。當m=n時所有的排列情況叫全排列。

公式：全排列數f(n)=n!(定義0!=1)

演算法：遞迴演算法=》網路上偷了一個圖

 

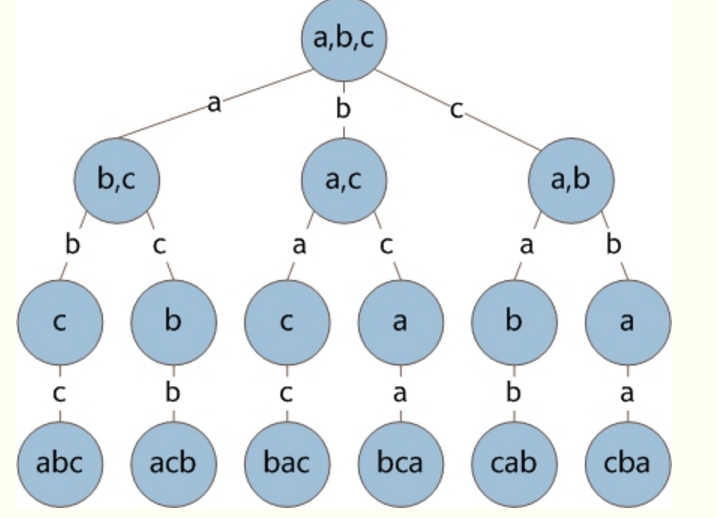
全排列：順便複習一個數學公式

排列的定義：從n個不同元素中，任取m(m≤n,m與n均為自然數,下同）個元素按照一定的順序排成一列，叫做從n個不同元素中取出m個元素的一個排列；從n個不同元素中取出m(m≤n）個元素的所有排列的個數，叫做從n個不同元素中取出m個元素的排列數，用符號 A(n,m）表示。

計算公式：

組合的定義：從n個不同元素中，任取m(m≤n）個元素併成一組，叫做從n個不同元素中取出m個元素的一個組合；從n個不同元素中取出m(m≤n）個元素的所有組合的個數，叫做從n個不同元素中取出m個元素的組合數。用符號 C(n,m) 表示。

計算公式：  ；C(n,m)=C(n,n-m）。（n≥m)

 

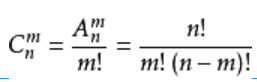
排列和組合的區別：

看問題是否和順序有關。有關就是排列，無關就是組合。 排列：比如說排隊問題甲乙兩人排隊，先排甲，那麼站法是甲乙，先排乙，那麼站法乙甲，是兩種不同的排法，和先排還是後排的順序有關，所以是A(2,2)=2種

組合：從甲乙兩個球中選2個，無論先取甲，在是先取乙，取到的兩個球都是甲和乙兩個球，和先後取的順序無關，所以是C(2,2)=1種

#include<iostream>
using namespace std;
//交換
void swap(int &a , int &b)
{
	int temp;
	temp = a;
	a = b;
	b = temp;
 } 
 //全排列遞迴演算法
void Perm(int list[] , int k ,int m) 
{
	//list 陣列存放排列的數，K表示層 代表第幾個數，m表示陣列的長度
	if(k==m)
	{
		//K==m 表示到達最後一個數，不能再交換，最終的排列的數需要輸出；
		for(int i=0 ;i<=m ;i++)
		 cout<<list[i];
		 cout<<endl; 
	 } 
	 else{
	 	for(int i=k;i<=m;i++)
	 	{
	 		swap(list[i],list[k]);
	 		Perm(list,k+1,m);
	 		swap(list[i] , list[k]);
		 }
	 }
	 
}
int main(void)
{
   int a[]={1,2,3};
   int m=2;
   Perm(a,0,2);
	/*
  123
  132
  213
  231
  321
  312
*/
 } 
 

演算法解析思路樹解釋

 

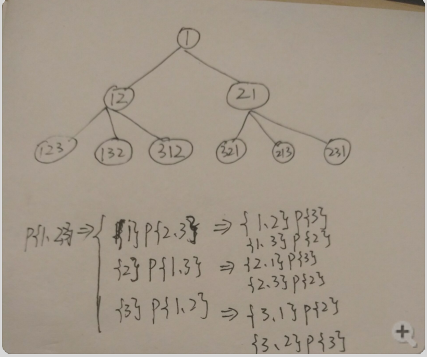
每次固定幾位數，最後只剩一位數，輸出，在從後面遞迴返回上一層，交換在輸出

        for(int i=k;i<=m;i++)

             {

                    swap(list[i],list[k]);

                    Perm(list,k+1,m);

                    swap(list[i] , list[k]);

               }

程式碼解析”” int i=k K表示固定了幾位數，當前陣列交換的臨界的位置

 1,2,3,4 當K=0的時候 {1,2,3,4} =》1是固定的 K+1遞迴

{1}p{2,3,4}，K=1，I=1 陣列交換隻能list[1],list[2],list[3]交換 k=i ,就是為了作為一個標識。